This is “Additional Complexities of Estimating Cash Flows”, section 8.6 from the book Accounting for Managers (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
8.6 Additional Complexities of Estimating Cash Flows
Learning Objective
- Evaluate investments with multiple investment and working capital cash flows.
Question: The examples in this chapter are intended to help you learn the basics of evaluating investments using the net present value (NPV), internal rate of return (IRR), and payback methods. However, there are two additional items related to estimating cash flows that must be considered: investment cash outflows and working capital. How do these two items impact long-term investment decisions?
Answer: These items impact the analysis of long-term investments as described next.
Investment Cash Outflows
The examples thus far have assumed that cash outflows for the investment occur only at the beginning of the investment. However, some investments require cash outflows at varying points throughout the life of the project. For example, suppose the JCPenney Company plans to open a new store, which requires a $10,000,000 investment at the beginning of the project for construction of the building. However, the building will be expanded at the end of year 4, at a cost of $2,000,000, to meet an expected increase in demand. The $2,000,000 cash outflow must be included in the cash flows of the project for year 4 when calculating the NPV, IRR, and payback period.
Working Capital
Working capitalCurrent assets minus current liabilities. is defined as current assets (cash, accounts receivable, inventory, and the like) minus current liabilities (accounts payable, wages payable, and accrued liabilities, for instance). Many long-term investments require working capital. For example, JCPenney will need cash in its registers when it opens the new store. Working capital is also required to fund inventory and accounts receivable. Working capital necessary for long-term investments should be included as a cash outflow, typically at the beginning of the project.
Some long-term investments have an expected life, at the end of which working capital is returned to the company for investment elsewhere. When this happens, the working capital is included in the cash flow analysis as a cash outflow at the beginning of the project and a cash inflow at the end of the project.
Key Takeaway
- Investment proposals often include investment cash outflows at varying points throughout the life of the project. These cash flows must be included when evaluating investment proposals using NPV, IRR, and payback period methods. Many investments include working capital cash flows required to fund items such as inventory and accounts receivable. Working capital is included as a cash outflow, typically at the beginning of the project, and is often returned back to the company as a cash inflow later in the project.
Review Problem 8.6
The management of Environmental Engineering, Inc. (EEI), would like to open an office for 6 years in a high-growth area of Las Vegas. The initial investment required to purchase an office building is $250,000, and EEI needs $50,000 in working capital for the new office. Working capital will be returned to EEI at the end of 6 years. EEI expects to remodel the office at the end of 3 years at a cost of $200,000. Annual net cash receipts from daily operations (cash receipts minus cash payments) are expected to be as follows:
| Year 1 | $ 60,000 |
| Year 2 | $ 80,000 |
| Year 3 | $120,000 |
| Year 4 | $150,000 |
| Year 5 | $160,000 |
| Year 6 | $110,000 |
Although the company’s cost of capital is 8 percent, management set a required rate of return of 12 percent due to the high risk associated with this project.
- Find the NPV of this investment using the format presented in Figure 8.2 "NPV Calculation for Copy Machine Investment by Jackson’s Quality Copies".
- Use trial and error to approximate the IRR for this investment proposal.
- Based on your answers to 1 and 2, should EEI open the new office? Explain.
- Use the format in Table 8.1 "Calculating the Payback Period for Jackson’s Quality Copies" to calculate the payback period.
Solution to Review Problem 8.6
-
The NPV is $27,571, as shown in the following figure.
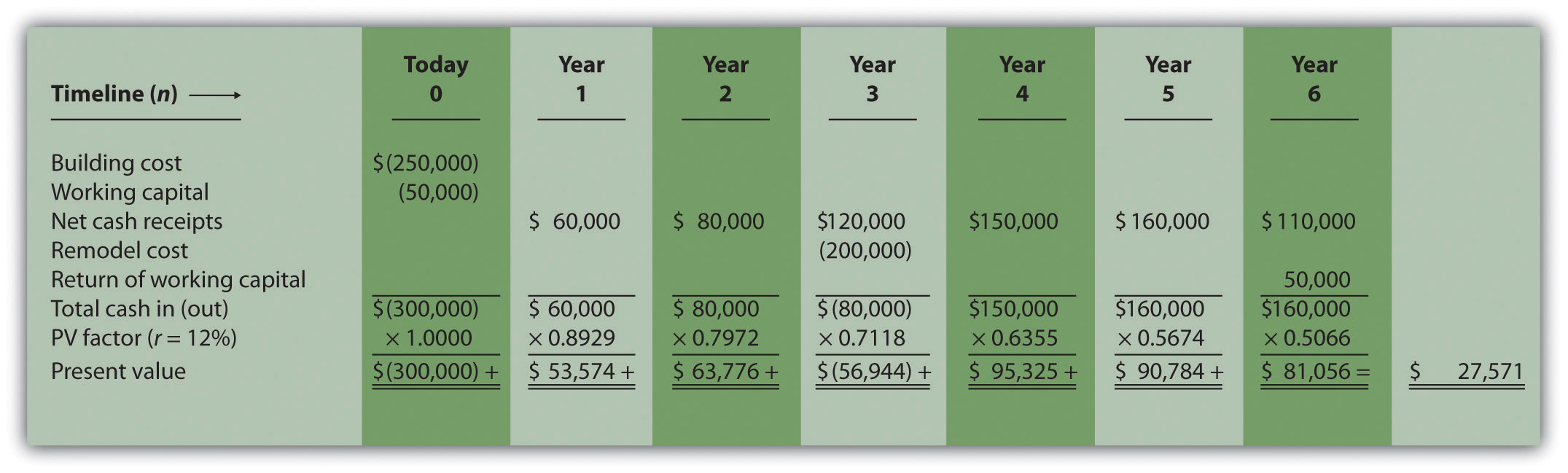
Note: The NPV is $27,571. Because NPV is > 0, accept the investment. (The investment provides a return greater than 12 percent.)
-
The IRR is between 14 and 15 percent (approximately 14.5 percent). The IRR is the rate that generates a NPV of zero. Because the NPV is positive at 12 percent, the return is higher than 12 percent. The NPV is calculated as follows using a rate of 14 percent, NPV = $5,007, and 15 percent, NPV = $(5,446). Thus the IRR is between 14 and 15 percent.
NPV at 14 percent is

NPV at 15 percent is

- Yes. The NPV is positive at $27,571, and the IRR of 14.5 percent is higher than the company’s required rate of return of 12 percent. Thus EEI should open the office in Las Vegas.
-
The payback period is approximately 4.5 years. This approximation assumes the $90,000 unrecovered investment at the end of year 4 will be recovered about halfway through year 5.
Investment (Cash Outflow) Cash Inflow Unrecovered Investment Balance Year 0 $(300,000) - $(300,000) Year 1 - $ 60,000 (240,000)a Year 2 - 80,000 (160,000)b Year 3 (200,000) 120,000 (240,000)c Year 4 - 150,000 (90,000) Year 5 - 160,000 0 Year 6 - 160,000 0 a $(240,000) = $(300,000) unrecovered investment + $60,000 year 1 cash inflow.
b $(160,000) = $(240,000) unrecovered investment at end of year 1 + $80,000 year 2 cash inflow.
c $(240,000) = $(160,000) unrecovered investment at end of year 2 – $200,000 year 3 investment + $120,000 year 3 cash inflow.
A more precise calculation can be performed assuming the $160,000 cash inflow for year 5 occurs evenly throughout the year. Simply calculate how many months are required in year 5 to recover the remaining $90,000. $90,000 divided by $160,000 equals 0.56 (rounded). Thus 0.56 of a year, or approximately 7 months (= 0.56 × 12 months), is required to recover the remaining $90,000. This more precise calculation results in a payback period of four years and seven months.




