This is “Chemical Kinetics”, chapter 14 from the book Principles of General Chemistry (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 14 Chemical Kinetics
The gases, liquids, solids, and solutions that you learned to describe quantitatively in Chapter 10 "Gases", Chapter 11 "Liquids", Chapter 12 "Solids", and Chapter 13 "Solutions", respectively, are systems whose chemical compositions do not change with time. Now we will present a quantitative description of a far more common situation in which the chemical composition of a system is not constant with time. An example of such a system is the stratosphere, where chemicals rising from the ground level initiate reactions that lead to decreases in the concentration of stratospheric ozone—the so-called ozone hole. (For more information about the ozone hole, see Chapter 3 "Chemical Reactions", Section 3.6 "Chemical Reactions in the Atmosphere".) Another example involves the production of polyethylene, in which the properties of the plastic are determined by the relative speeds of events that occur during the polymerization reaction. (For more information about the polymerization reaction, see Chapter 12 "Solids", Section 12.8 "Polymeric Solids".) The techniques you are about to learn will enable you to describe the speed of many such changes and predict how the composition of each system will change in response to changing conditions.
The Belousov-Zhabotinsky reaction, a chemical reaction that oscillates in time and space. When a very thin layer of an acidic solution containing potassium bromate (KBrO3), cerium ammonium nitrate [(NH4)2Ce(NO3)6], malonic acid (HO2CCH2CO2H), and an indicator is poured into a shallow dish, local fluctuations in the concentration of the reactants and a complex series of reactions cause striking geometric patterns of concentric circles and spirals to propagate across the dish.
We begin Chapter 14 "Chemical Kinetics" with a discussion of chemical kineticsThe study of reaction rates., which is the study of reaction ratesThe changes in concentrations of reactants and products with time., or the changes in the concentrations of reactants and products with time. As you learn about the factors that affect reaction rates, the methods chemists use for reporting and calculating those rates, and the clues that reaction rates provide about events at the molecular level, you will also discover the answers to questions such as the following: How can normally stable substances such as flour and coal cause devastating explosions? How do archaeologists use isotopic composition to estimate the ages of ancient artifacts? How do the catalysts used in catalytic converters, some laundry detergents, and meat tenderizers work?
Summary
Chemical kinetics is the study of reaction rates, the changes in the concentrations of reactants and products with time.
14.1 Factors That Affect Reaction Rates
Learning Objective
- To understand the factors that affect reaction rates.
Although a balanced chemical equation for a reaction describes the quantitative relationships between the amounts of reactants present and the amounts of products that can be formed, it gives us no information about whether or how fast a given reaction will occur. This information is obtained by studying the chemical kinetics of a reaction, which depend on various factors: reactant concentrations, temperature, physical states and surface areas of reactants, and solvent and catalyst properties if either are present. By studying the kinetics of a reaction, chemists gain insights into how to control reaction conditions to achieve a desired outcome.
Concentration Effects
Two substances cannot possibly react with each other unless their constituent particles (molecules, atoms, or ions) come into contact. If there is no contact, the reaction rate will be zero. Conversely, the more reactant particles that collide per unit time, the more often a reaction between them can occur. Consequently, the reaction rate usually increases as the concentration of the reactants increases. One example of this effect is the reaction of sucrose (table sugar) with sulfuric acid, which is shown in Figure 14.1 "The Effect of Concentration on Reaction Rates".
Figure 14.1 The Effect of Concentration on Reaction Rates

Mixing sucrose with dilute sulfuric acid in a beaker (a, right) produces a simple solution. Mixing the same amount of sucrose with concentrated sulfuric acid (a, left) results in a dramatic reaction (b) that eventually produces a column of black porous graphite (c) and an intense smell of burning sugar.
Temperature Effects
You learned in Chapter 10 "Gases" that increasing the temperature of a system increases the average kinetic energy of its constituent particles. As the average kinetic energy increases, the particles move faster, so they collide more frequently per unit time and possess greater energy when they collide. Both of these factors increase the reaction rate. Hence the reaction rate of virtually all reactions increases with increasing temperature. Conversely, the reaction rate of virtually all reactions decreases with decreasing temperature. For example, refrigeration retards the rate of growth of bacteria in foods by decreasing the reaction rates of biochemical reactions that enable bacteria to reproduce. Figure 14.2 "The Effect of Temperature on Reaction Rates" shows how temperature affects the light emitted by two chemiluminescent light sticks.
Figure 14.2 The Effect of Temperature on Reaction Rates

At high temperature, the reaction that produces light in a chemiluminescent light stick occurs more rapidly, producing more photons of light per unit time. Consequently, the light glows brighter in hot water (left) than in ice water (right).
In systems where more than one reaction is possible, the same reactants can produce different products under different reaction conditions. For example, in the presence of dilute sulfuric acid and at temperatures around 100°C, ethanol is converted to diethyl ether:
Equation 14.1
At 180°C, however, a completely different reaction occurs, which produces ethylene as the major product:
Equation 14.2
Phase and Surface Area Effects
When two reactants are in the same fluid phase, their particles collide more frequently than when one or both reactants are solids (or when they are in different fluids that do not mix). If the reactants are uniformly dispersed in a single homogeneous solution, then the number of collisions per unit time depends on concentration and temperature, as we have just seen. If the reaction is heterogeneous, however, the reactants are in two different phases, and collisions between the reactants can occur only at interfaces between phases. The number of collisions between reactants per unit time is substantially reduced relative to the homogeneous case, and, hence, so is the reaction rate. The reaction rate of a heterogeneous reaction depends on the surface area of the more condensed phase.
Automobile engines use surface area effects to increase reaction rates. Gasoline is injected into each cylinder, where it combusts on ignition by a spark from the spark plug. The gasoline is injected in the form of microscopic droplets because in that form it has a much larger surface area and can burn much more rapidly than if it were fed into the cylinder as a stream. Similarly, a pile of finely divided flour burns slowly (or not at all), but spraying finely divided flour into a flame produces a vigorous reaction (Figure 14.3 "The Effect of Surface Area on Reaction Rates"). Similar phenomena are partially responsible for dust explosions that occasionally destroy grain elevators or coal mines.
Figure 14.3 The Effect of Surface Area on Reaction Rates

A pile of flour is only scorched by a flame (right), but when the same flour is sprayed into the flame, it burns rapidly (left).
Solvent Effects
The nature of the solvent can also affect the reaction rates of solute particles. For example, a sodium acetate solution reacts with methyl iodide in an exchange reaction to give methyl acetate and sodium iodide.
Equation 14.3
CH3CO2Na(soln) + CH3I(l) → CH3CO2CH3(soln) + NaI(soln)This reaction occurs 10 million times more rapidly in the organic solvent dimethylformamide [DMF; (CH3)2NCHO] than it does in methanol (CH3OH). Although both are organic solvents with similar dielectric constants (36.7 for DMF versus 32.6 for methanol), methanol is able to hydrogen bond with acetate ions, whereas DMF cannot. Hydrogen bonding reduces the reactivity of the oxygen atoms in the acetate ion.
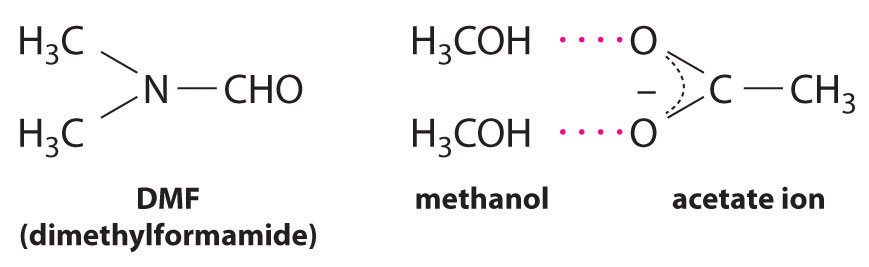
Solvent viscosity is also important in determining reaction rates. In highly viscous solvents, dissolved particles diffuse much more slowly than in less viscous solvents and can collide less frequently per unit time. Thus the reaction rates of most reactions decrease rapidly with increasing solvent viscosity.
Catalyst Effects
You learned in Chapter 3 "Chemical Reactions" that a catalyst is a substance that participates in a chemical reaction and increases the reaction rate without undergoing a net chemical change itself. Consider, for example, the decomposition of hydrogen peroxide in the presence and absence of different catalysts (Figure 14.4 "The Effect of Catalysts on Reaction Rates"). Because most catalysts are highly selective, they often determine the product of a reaction by accelerating only one of several possible reactions that could occur.
Figure 14.4 The Effect of Catalysts on Reaction Rates

A solution of hydrogen peroxide (H2O2) decomposes in water so slowly that the change is not noticeable (left). Iodide ion acts as a catalyst for the decomposition of H2O2, producing oxygen gas. The solution turns brown because of the reaction of H2O2 with I−, which generates small amounts of I3− (center). The enzyme catalase is about 3 billion times more effective than iodide as a catalyst. Even in the presence of very small amounts of enzyme, the decomposition is vigorous (right).
Most of the bulk chemicals produced in industry are formed with catalyzed reactions. Recent estimates indicate that about 30% of the gross national product of the United States and other industrialized nations relies either directly or indirectly on the use of catalysts.
Summary
Factors that influence the reaction rates of chemical reactions include the concentration of reactants, temperature, the physical state of reactants and their dispersion, the solvent, and the presence of a catalyst.
Key Takeaway
- The reaction rate depends on the concentrations of the reactants, the temperature of the reaction, the phase and surface area of the reactants, the solvent, and the presence or the absence of a catalyst.
Conceptual Problems
-
What information can you obtain by studying the chemical kinetics of a reaction? Does a balanced chemical equation provide the same information? Why or why not?
-
If you were tasked with determining whether to proceed with a particular reaction in an industrial facility, why would studying the chemical kinetics of the reaction be important to you?
-
What is the relationship between each of the following factors and the reaction rate: reactant concentration, temperature of the reaction, physical properties of the reactants, physical and chemical properties of the solvent, and the presence of a catalyst?
-
A slurry is a mixture of a finely divided solid with a liquid in which it is only sparingly soluble. As you prepare a reaction, you notice that one of your reactants forms a slurry with the solvent, rather than a solution. What effect will this have on the reaction rate? What steps can you take to try to solve the problem?
-
Why does the reaction rate of virtually all reactions increase with an increase in temperature? If you were to make a glass of sweetened iced tea the old-fashioned way, by adding sugar and ice cubes to a glass of hot tea, which would you add first?
-
In a typical laboratory setting, a reaction is carried out in a ventilated hood with air circulation provided by outside air. A student noticed that a reaction that gave a high yield of a product in the winter gave a low yield of that same product in the summer, even though his technique did not change and the reagents and concentrations used were identical. What is a plausible explanation for the different yields?
-
A very active area of chemical research involves the development of solubilized catalysts that are not made inactive during the reaction process. Such catalysts are expected to increase reaction rates significantly relative to the same reaction run in the presence of a heterogeneous catalyst. What is the reason for anticipating that the relative rate will increase?
-
Water has a dielectric constant more than two times greater than that of methanol (80.1 for H2O and 33.0 for CH3OH). Which would be your solvent of choice for a substitution reaction between an ionic compound and a polar reagent, both of which are soluble in either methanol or water? Why?
Answers
-
Kinetics gives information on the reaction rate and reaction mechanism; the balanced chemical equation gives only the stoichiometry of the reaction.
-
-
Reaction rates generally increase with increasing reactant concentration, increasing temperature, and the addition of a catalyst. Physical properties such as high solubility also increase reaction rates. Solvent polarity can either increase or decrease the reaction rate of a reaction, but increasing solvent viscosity generally decreases reaction rates.
-
-
Increasing the temperature increases the average kinetic energy of molecules and ions, causing them to collide more frequently and with greater energy, which increases the reaction rate. First dissolve sugar in the hot tea, and then add the ice.
-
-
-
14.2 Reaction Rates and Rate Laws
Learning Objectives
- To determine the reaction rate.
- To understand the meaning of a rate law.
The factors discussed in Section 14.1 "Factors That Affect Reaction Rates" affect the reaction rate of a chemical reaction, which may determine whether a desired product is formed. In this section, we will show you how to quantitatively determine the reaction rate.
Reaction Rates
Reaction rates are usually expressed as the concentration of reactant consumed or the concentration of product formed per unit time. The units are thus moles per liter per unit time, written as M/s, M/min, or M/h. To measure reaction rates, chemists initiate the reaction, measure the concentration of the reactant or product at different times as the reaction progresses, perhaps plot the concentration as a function of time on a graph, and then calculate the change in the concentration per unit time.
The progress of a simple reaction (A → B) is shown in Figure 14.5 "The Progress of a Simple Reaction (A → B)", where the beakers are snapshots of the composition of the solution at 10 s intervals. The number of molecules of reactant (A) and product (B) are plotted as a function of time in the graph. Each point in the graph corresponds to one beaker in Figure 14.5 "The Progress of a Simple Reaction (A → B)". The reaction rate is the change in the concentration of either the reactant or the product over a period of time. The concentration of A decreases with time, while the concentration of B increases with time.
Figure 14.5 The Progress of a Simple Reaction (A → B)
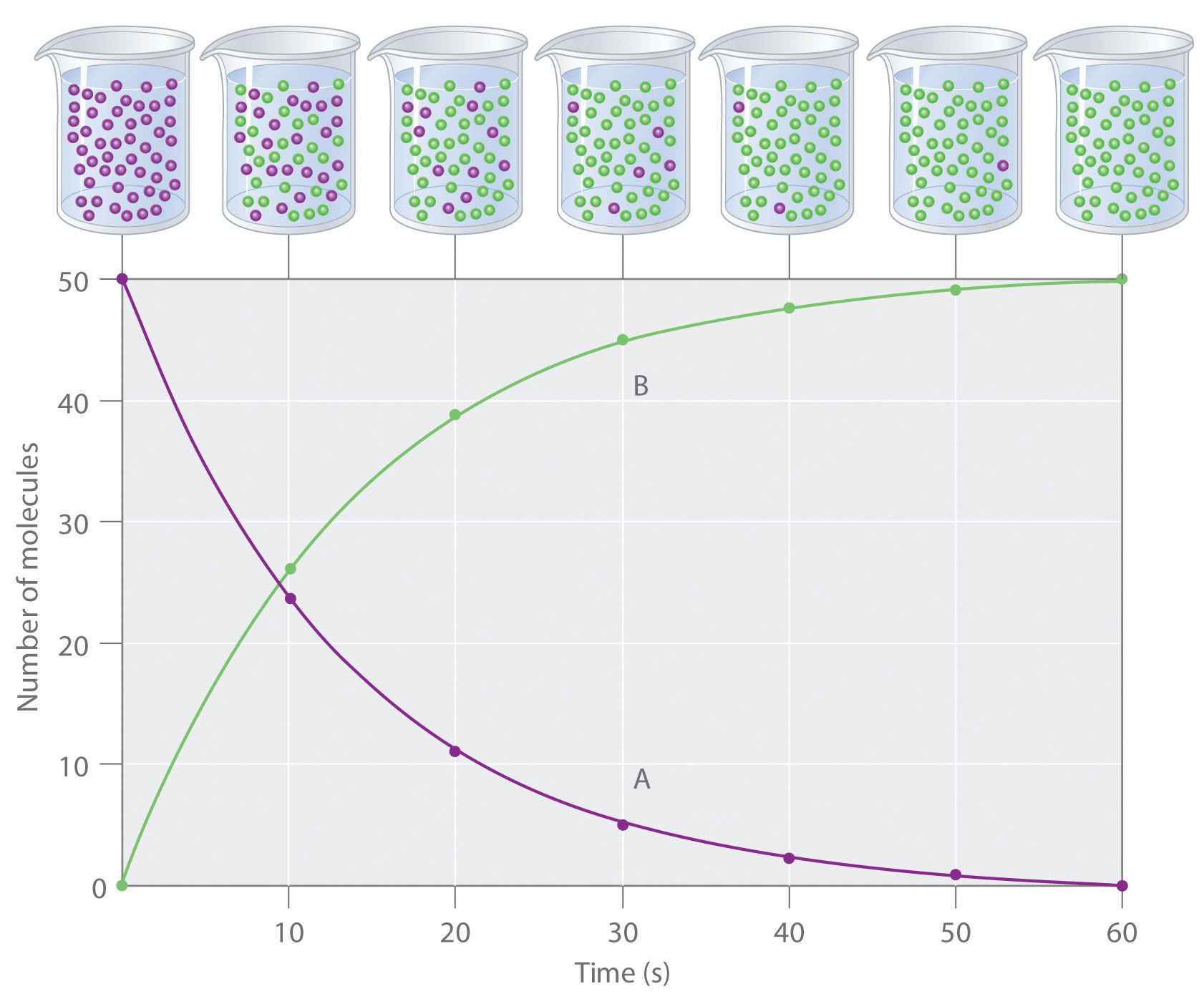
The mixture initially contains only A molecules (purple). With increasing time, the number of A molecules decreases and more B molecules (green) are formed (top). The graph shows the change in the number of A and B molecules in the reaction as a function of time over a 1 min period (bottom).
Equation 14.4
Just as in Chapter 4 "Reactions in Aqueous Solution" and Chapter 5 "Energy Changes in Chemical Reactions", square brackets indicate molar concentrations, and the capital Greek delta (Δ) means “change in.” Because chemists follow the convention of expressing all reaction rates as positive numbers, however, a negative sign is inserted in front of Δ[A]/Δt to convert that expression to a positive number. The reaction rate we would calculate for the reaction A → B using Equation 14.4 would be different for each interval. (This is not true for every reaction, as you will see later.) A much greater change occurs in [A] and [B] during the first 10 s interval, for example, than during the last, which means that the reaction rate is fastest at first. This is consistent with the concentration effects described in Section 14.1 "Factors That Affect Reaction Rates" because the concentration of A is greatest at the beginning of the reaction.
Note the Pattern
Reaction rates generally decrease with time as reactant concentrations decrease.
Determining the Reaction Rate of Hydrolysis of Aspirin
We can use Equation 14.4 to determine the reaction rate of hydrolysis of aspirin, probably the most commonly used drug in the world. (More than 25,000,000 kg are produced annually worldwide.) Aspirin (acetylsalicylic acid) reacts with water (such as water in body fluids) to give salicylic acid and acetic acid.
Figure 14.6
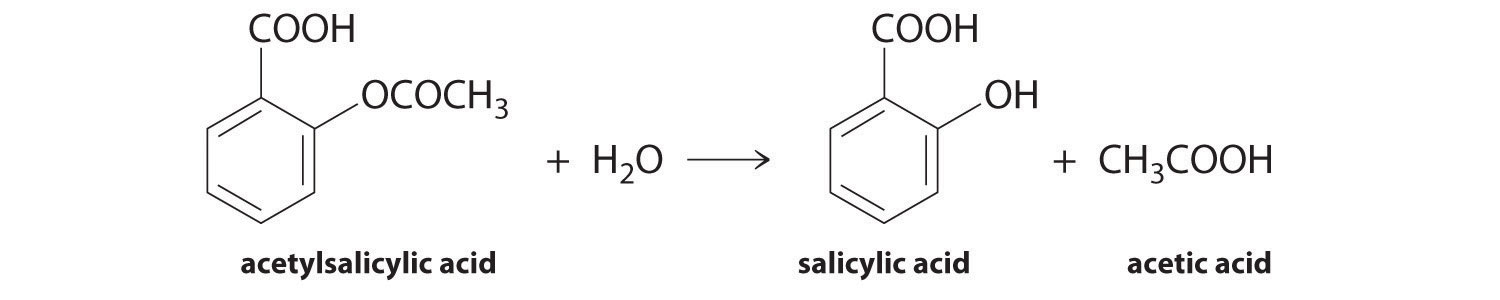
Because salicylic acid is the actual substance that relieves pain and reduces fever and inflammation, a great deal of research has focused on understanding this reaction and the factors that affect its rate. Data for the hydrolysis of a sample of aspirin are in Table 14.1 "Data for Aspirin Hydrolysis in Aqueous Solution at pH 7.0 and 37°C*" and are shown in the graph in Figure 14.7 "The Hydrolysis of Aspirin". These data were obtained by removing samples of the reaction mixture at the indicated times and analyzing them for the concentrations of the reactant (aspirin) and one of the products (salicylic acid).
Table 14.1 Data for Aspirin Hydrolysis in Aqueous Solution at pH 7.0 and 37°C*
| Time (h) | [Aspirin] (M) | [Salicylic Acid] (M) |
|---|---|---|
| 0 | 5.55 × 10−3 | 0 |
| 2.0 | 5.51 × 10−3 | 0.040 × 10−3 |
| 5.0 | 5.45 × 10−3 | 0.10 × 10−3 |
| 10 | 5.35 × 10−3 | 0.20 × 10−3 |
| 20 | 5.15 × 10−3 | 0.40 × 10−3 |
| 30 | 4.96 × 10−3 | 0.59 × 10−3 |
| 40 | 4.78 × 10−3 | 0.77 × 10−3 |
| 50 | 4.61 × 10−3 | 0.94 × 10−3 |
| 100 | 3.83 × 10−3 | 1.72 × 10−3 |
| 200 | 2.64 × 10−3 | 2.91 × 10−3 |
| 300 | 1.82 × 10−3 | 3.73 × 10−3 |
| *The reaction at pH 7.0 is very slow. It is much faster under acidic conditions, such as those found in the stomach. | ||
Figure 14.7 The Hydrolysis of Aspirin
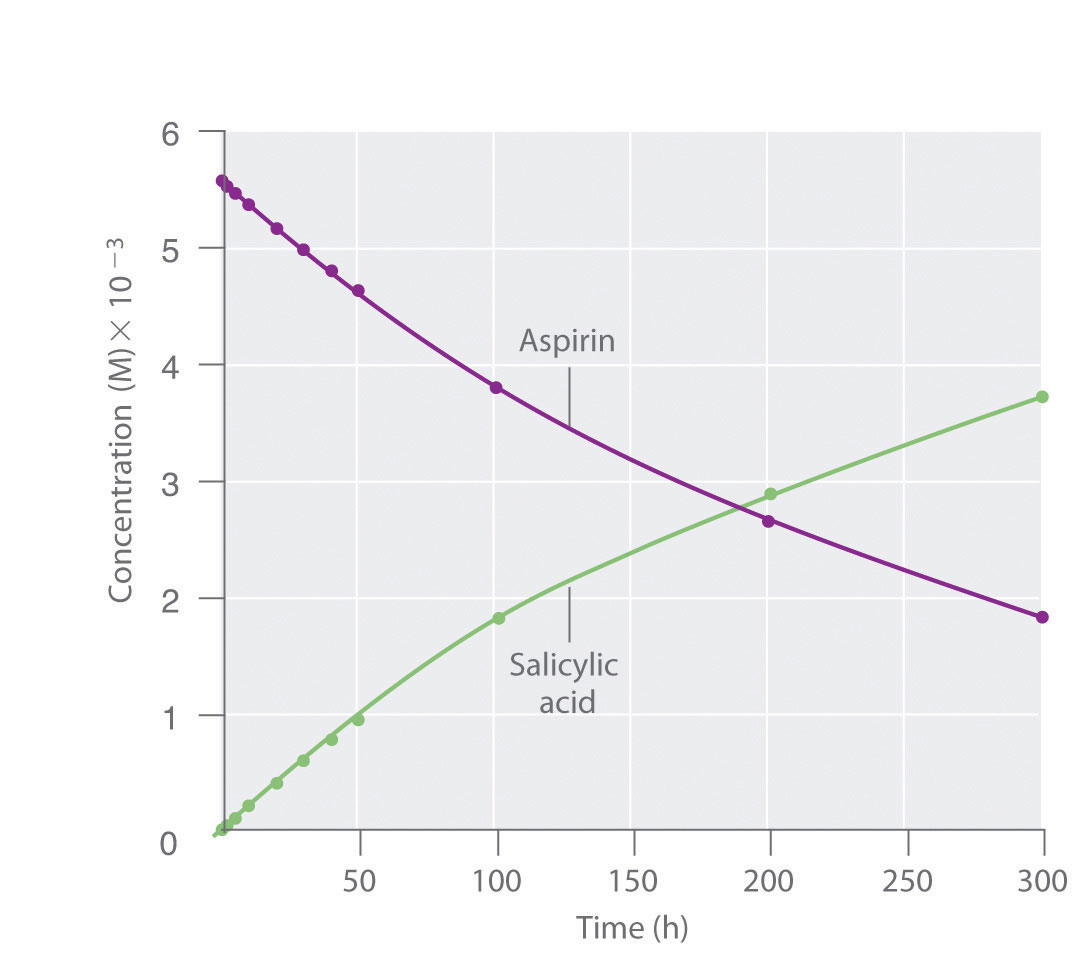
This graph shows the concentrations of aspirin and salicylic acid as a function of time, based on the hydrolysis data in Table 14.1 "Data for Aspirin Hydrolysis in Aqueous Solution at pH 7.0 and 37°C*". The time dependence of the concentration of the other product, acetate, is not shown, but based on the stoichiometry of the reaction, it is identical to the data for salicylic acid.
We can calculate the average reaction rateThe reaction rate calculated for a given time interval from the concentrations of either the reactant or one of the products at the beginning of the interval time and at the end of the interval for a given time interval from the concentrations of either the reactant or one of the products at the beginning of the interval (time = t0) and at the end of the interval (t1). Using salicylic acid, for example, we find the reaction rate for the interval between t = 0 h and t = 2.0 h (recall that change is always calculated as final minus initial):
We can also calculate the reaction rate from the concentrations of aspirin at the beginning and the end of the same interval, remembering to insert a negative sign, because its concentration decreases:
If we now calculate the reaction rate during the last interval given in Table 14.1 "Data for Aspirin Hydrolysis in Aqueous Solution at pH 7.0 and 37°C*" (the interval between 200 h and 300 h after the start of the reaction), we find that the reaction rate is significantly slower than it was during the first interval (t = 0–2.0 h):
(You should verify from the data in Table 14.1 "Data for Aspirin Hydrolysis in Aqueous Solution at pH 7.0 and 37°C*" that you get the same rate using the concentrations of aspirin measured at 200 h and 300 h.)
Calculating the Reaction Rate of Fermentation of Sucrose
In the preceding example, the stoichiometric coefficients in the balanced chemical equation are the same for all reactants and products; that is, the reactants and products all have the coefficient 1. Let us look at a reaction in which the coefficients are not all the same: the fermentation of sucrose to ethanol and carbon dioxide, which we encountered in Chapter 3 "Chemical Reactions".
Equation 14.5
The coefficients show us that the reaction produces four molecules of ethanol and four molecules of carbon dioxide for every one molecule of sucrose consumed. As before, we can find the reaction rate by looking at the change in the concentration of any reactant or product. In this particular case, however, a chemist would probably use the concentration of either sucrose or ethanol because gases are usually measured as volumes and, as you learned in Chapter 10 "Gases", the volume of CO2 gas formed will depend on the total volume of the solution being studied and the solubility of the gas in the solution, not just the concentration of sucrose. The coefficients in the balanced chemical equation tell us that the reaction rate at which ethanol is formed is always four times faster than the reaction rate at which sucrose is consumed:
Equation 14.6
The concentration of the reactant—in this case sucrose—decreases with increasing time, so the value of Δ[sucrose] is negative. Consequently, a minus sign is inserted in front of Δ[sucrose] in Equation 14.6 so that the rate of change of the sucrose concentration is expressed as a positive value. Conversely, the ethanol concentration increases with increasing time, so its rate of change is automatically expressed as a positive value.
Often the reaction rate is expressed in terms of the reactant or product that has the smallest coefficient in the balanced chemical equation. The smallest coefficient in the sucrose fermentation reaction (Equation 14.5) corresponds to sucrose, so the reaction rate is generally defined as follows:
Equation 14.7
Example 1
Consider the thermal decomposition of gaseous N2O5 to NO2 and O2 via the following equation:
Write expressions for the reaction rate in terms of the rates of change in the concentrations of the reactant and each product with time.
Given: balanced chemical equation
Asked for: reaction rate expressions
Strategy:
A Choose the species in the equation that has the smallest coefficient. Then write an expression for the rate of change of that species with time.
B For the remaining species in the equation, use molar ratios to obtain equivalent expressions for the reaction rate.
Solution:
A Because O2 has the smallest coefficient in the balanced chemical equation for the reaction, we define the reaction rate as the rate of change in the concentration of O2 and write that expression.
B We know from the balanced chemical equation that 2 mol of N2O5 must decompose for each 1 mol of O2 produced and that 4 mol of NO2 are produced for every 1 mol of O2 produced. The molar ratios of O2 to N2O5 and to NO2 are thus 1:2 and 1:4, respectively. This means that we divide the rate of change of [N2O5] and [NO2] by its stoichiometric coefficient to obtain equivalent expressions for the reaction rate. For example, because NO2 is produced at four times the rate of O2, we must divide the rate of production of NO2 by 4. The reaction rate expressions are as follows:
Exercise
The key step in the industrial production of sulfuric acid is the reaction of SO2 with O2 to produce SO3.
2SO2(g) + O2(g) → 2SO3(g)Write expressions for the reaction rate in terms of the rate of change of the concentration of each species.
Answer:
Example 2
Using the reaction shown in Example 1, calculate the reaction rate from the following data taken at 56°C:
| 2N2O5(g) → 4NO2(g) + O2(g) | |||
|---|---|---|---|
| Time (s) | [N2O5] (M) | [NO2] (M) | [O2] (M) |
| 240 | 0.0388 | 0.0314 | 0.00792 |
| 600 | 0.0197 | 0.0699 | 0.0175 |
Given: balanced chemical equation and concentrations at specific times
Asked for: reaction rate
Strategy:
A Using the equations in Example 1, subtract the initial concentration of a species from its final concentration and substitute that value into the equation for that species.
B Substitute the value for the time interval into the equation. Make sure your units are consistent.
Solution:
A We are asked to calculate the reaction rate in the interval between t1 = 240 s and t2 = 600 s. From Example 1, we see that we can evaluate the reaction rate using any of three expressions:
Subtracting the initial concentration from the final concentration of N2O5 and inserting the corresponding time interval into the rate expression for N2O5,
B Substituting actual values into the expression,
Similarly, we can use NO2 to calculate the reaction rate:
If we allow for experimental error, this is the same rate we obtained using the data for N2O5, as it should be because the reaction rate should be the same no matter which concentration is used. We can also use the data for O2:
Again, this is the same value we obtained from the N2O5 and NO2 data. Thus the reaction rate does not depend on which reactant or product is used to measure it.
Exercise
Using the data in the following table, calculate the reaction rate of SO2(g) with O2(g) to give SO3(g).
| 2SO2(g) + O2(g) → 2SO3(g) | |||
|---|---|---|---|
| Time (s) | [SO2] (M) | [O2] (M) | [SO3] (M) |
| 300 | 0.0270 | 0.0500 | 0.0072 |
| 720 | 0.0194 | 0.0462 | 0.0148 |
Answer: 9.0 × 10−6 M/s
Instantaneous Rates of Reaction
So far, we have determined average reaction rates over particular intervals of time. We can also determine the instantaneous rateThe reaction rate of a chemical reaction at any given point in time. of a reaction, which is the reaction rate at any given point in time. As the period of time used to calculate an average rate of a reaction becomes shorter and shorter, the average rate approaches the instantaneous rate.If you have studied calculus, you may recognize that the instantaneous rate of a reaction at a given time corresponds to the slope of a line tangent to the concentration-versus-time curve at that point—that is, the derivative of concentration with respect to time.
Think of the distinction between the instantaneous and average rates of a reaction as being similar to the distinction between the actual speed of a car at any given time on a trip and the average speed of the car for the entire trip. Although you may travel for a long time at 65 mph on an interstate highway during a long trip, there may be times when you travel only 25 mph in construction zones or 0 mph if you stop for meals or gas. Thus your average speed on the trip may be only 50 mph, whereas your instantaneous speed on the interstate at a given moment may be 65 mph. Whether you are able to stop the car in time to avoid an accident depends on your instantaneous speed, not your average speed. There are important differences between the speed of a car during a trip and the speed of a chemical reaction, however. The speed of a car may vary unpredictably over the length of a trip, and the initial part of a trip is often one of the slowest. In a chemical reaction, the initial interval normally has the fastest rate (though this is not always the case), and the reaction rate generally changes smoothly over time.
In chemical kinetics, we generally focus on one particular instantaneous rate, which is the initial reaction rate, t = 0. Initial rates are determined by measuring the reaction rate at various times and then extrapolating a plot of rate versus time to t = 0.
Rate Laws
In Section 14.1 "Factors That Affect Reaction Rates", you learned that reaction rates generally decrease with time because reactant concentrations decrease as reactants are converted to products. You also learned that reaction rates generally increase when reactant concentrations are increased. We now examine the mathematical expressions called rate lawsMathematical expressions that describe the relationships between reactant rates and reactant concentrations in a chemical reaction., which describe the relationships between reactant rates and reactant concentrations. Rate laws are laws as defined in Chapter 1 "Introduction to Chemistry"; that is, they are mathematical descriptions of experimentally verifiable data.
Rate laws may be written from either of two different but related perspectives. A differential rate lawA rate law that expresses the reaction rate in terms of changes in the concentration of one or more reactants (Δ[R]) over a specific time interval expresses the reaction rate in terms of changes in the concentration of one or more reactants (Δ[R]) over a specific time interval (Δt). In contrast, an integrated rate lawA rate law that expresses the reaction rate in terms of the initial concentration and the measured concentration of one or more reactants ([R]) after a given amount of time describes the reaction rate in terms of the initial concentration ([R]0) and the measured concentration of one or more reactants ([R]) after a given amount of time (t); we will discuss integrated rate laws in Section 14.3 "Methods of Determining Reaction Order". The integrated rate law can be found by using calculus to integrate the differential rate law, although the method of doing so is beyond the scope of this text. Whether you use a differential rate law or integrated rate law, always make sure that the rate law gives the proper units for the reaction rate, usually moles per liter per second (M/s).
Reaction Orders
For a reaction with the general equation
Equation 14.8
aA + bB → cC + dDthe experimentally determined rate law usually has the following form:
Equation 14.9
rate = k[A]m[B]nThe proportionality constant (k) is called the rate constantA proportionality constant whose value is characteristic of the reaction and the reaction conditions and whose numerical value does not change as the reaction progresses under a given set of conditions., and its value is characteristic of the reaction and the reaction conditions. A given reaction has a particular value of the rate constant under a given set of conditions, such as temperature, pressure, and solvent; varying the temperature or the solvent usually changes the value of the rate constant. The numerical value of k, however, does not change as the reaction progresses under a given set of conditions.
Thus the reaction rate depends on the rate constant for the given set of reaction conditions and the concentration of A and B raised to the powers m and n, respectively. The values of m and n are derived from experimental measurements of the changes in reactant concentrations over time and indicate the reaction orderNumbers that indicate the degree to which the reaction rate depends on the concentration of each reactant., the degree to which the reaction rate depends on the concentration of each reactant; m and n need not be integers. For example, Equation 14.9 tells us that Equation 14.8 is mth order in reactant A and nth order in reactant B. It is important to remember that n and m are not related to the stoichiometric coefficients a and b in the balanced chemical equation and must be determined experimentally. The overall reaction order is the sum of all the exponents in the rate law: m + n.
Note the Pattern
Under a given set of conditions, the value of the rate constant does not change as the reaction progresses.
Although differential rate laws are generally used to describe what is occurring on a molecular level during a reaction, integrated rate laws are used to determine the reaction order and the value of the rate constant from experimental measurements. (We present general forms for integrated rate laws in Section 14.3 "Methods of Determining Reaction Order".) To illustrate how chemists interpret a differential rate law, we turn to the experimentally derived rate law for the hydrolysis of t-butyl bromide in 70% aqueous acetone. This reaction produces t-butanol according to the following equation:
Equation 14.10
(CH3)3CBr(soln) + H2O(soln) → (CH3)3COH(soln) + HBr(soln)Combining the rate expression in Equation 14.4 and Equation 14.9 gives us a general expression for the differential rate law:
Equation 14.11
Inserting the identities of the reactants into Equation 14.11 gives the following expression for the differential rate law for the reaction:
Equation 14.12
Experiments done to determine the rate law for the hydrolysis of t-butyl bromide show that the reaction rate is directly proportional to the concentration of (CH3)3CBr but is independent of the concentration of water. Thus m and n in Equation 14.12 are 1 and 0, respectively, and
Equation 14.13
rate = k[(CH3)3CBr]1[H2O]0 = k[(CH3)3CBr]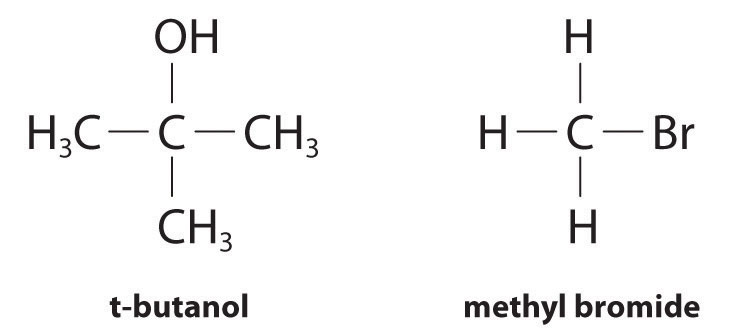
Because the exponent for the reactant is 1, the reaction is first order in (CH3)3CBr. It is zeroth order in water because the exponent for [H2O] is 0. (Recall that anything raised to the zeroth power equals 1.) Thus the overall reaction order is 1 + 0 = 1. What the reaction orders tell us in practical terms is that doubling the concentration of (CH3)3CBr doubles the reaction rate of the hydrolysis reaction, halving the concentration of (CH3)3CBr halves the reaction rate, and so on. Conversely, increasing or decreasing the concentration of water has no effect on the reaction rate. (Again, when you work with rate laws, there is no simple correlation between the stoichiometry of the reaction and the rate law. The values of k, m, and n in the rate law must be determined experimentally.) Experimental data show that k has the value 5.15 × 10−4 s−1 at 25°C. The rate constant has units of reciprocal seconds (s−1) because the reaction rate is defined in units of concentration per unit time (M/s). The units of a rate constant depend on the rate law for a particular reaction.
Under conditions identical to those for the t-butyl bromide reaction, the experimentally derived differential rate law for the hydrolysis of methyl bromide (CH3Br) is as follows:
Equation 14.14
This reaction also has an overall reaction order of 1, but the rate constant in Equation 14.14 is approximately 106 times smaller than that for t-butyl bromide. Thus methyl bromide hydrolyzes about 1 million times more slowly than t-butyl bromide, and this information tells chemists how the reactions differ on a molecular level.
Frequently, changes in reaction conditions also produce changes in a rate law. In fact, chemists often change reaction conditions to obtain clues about what is occurring during a reaction. For example, when t-butyl bromide is hydrolyzed in an aqueous acetone solution containing OH− ions rather than in aqueous acetone alone, the differential rate law for the hydrolysis reaction does not change. For methyl bromide, in contrast, the differential rate law becomes rate = k″[CH3Br][OH−], with an overall reaction order of 2. Although the two reactions proceed similarly in neutral solution, they proceed very differently in the presence of a base, which again provides clues as to how the reactions differ on a molecular level.
Note the Pattern
Differential rate laws are generally used to describe what is occurring on a molecular level during a reaction, whereas integrated rate laws are used for determining the reaction order and the value of the rate constant from experimental measurements.
Example 3
We present three reactions and their experimentally determined differential rate laws. For each reaction, give the units of the rate constant, give the reaction order with respect to each reactant, give the overall reaction order, and predict what happens to the reaction rate when the concentration of the first species in each chemical equation is doubled.
Given: balanced chemical equations and differential rate laws
Asked for: units of rate constant, reaction orders, and effect of doubling reactant concentration
Strategy:
A Express the reaction rate as moles per liter per second [mol/(L·s), or M/s]. Then determine the units of each chemical species in the rate law. Divide the units for the reaction rate by the units for all species in the rate law to obtain the units for the rate constant.
B Identify the exponent of each species in the rate law to determine the reaction order with respect to that species. Sum all exponents to obtain the overall reaction order.
C Use the mathematical relationships as expressed in the rate law to determine the effect of doubling the concentration of a single species on the reaction rate.
Solution:
-
A [HI]2 will give units of (moles per liter)2. For the reaction rate to have units of moles per liter per second, the rate constant must have reciprocal units [1/(M·s)]:
B The exponent in the rate law is 2, so the reaction is second order in HI. Because HI is the only reactant and the only species that appears in the rate law, the reaction is also second order overall.
C If the concentration of HI is doubled, the reaction rate will increase from k[HI]02 to k(2[HI])02 = 4k[HI]02. The reaction rate will therefore quadruple.
-
A Because no concentration term appears in the rate law, the rate constant must have M/s units for the reaction rate to have M/s units.
B The rate law tells us that the reaction rate is constant and independent of the N2O concentration. That is, the reaction is zeroth order in N2O and zeroth order overall.
C Because the reaction rate is independent of the N2O concentration, doubling the concentration will have no effect on the reaction rate.
-
A The rate law contains only one concentration term raised to the first power. Hence the rate constant must have units of reciprocal seconds (s−1) to have units of moles per liter per second for the reaction rate: M·s−1 = M/s.
B The only concentration in the rate law is that of cyclopropane, and its exponent is 1. This means that the reaction is first order in cyclopropane. Cyclopropane is the only species that appears in the rate law, so the reaction is also first order overall.
C Doubling the initial cyclopropane concentration will increase the reaction rate from k[cyclopropane]0 to 2k[cyclopropane]0. This doubles the reaction rate.
Exercise
Given the following two reactions and their experimentally determined differential rate laws: determine the units of the rate constant if time is in seconds, determine the reaction order with respect to each reactant, give the overall reaction order, and predict what will happen to the reaction rate when the concentration of the first species in each equation is doubled.
Answer:
- s−1; first order in CH3N=NCH3; first order overall; doubling [CH3N=NCH3] will double the reaction rate.
- M−1·s−1; first order in NO2, first order in F2; second order overall; doubling [NO2] will double the reaction rate.
Summary
Reaction rates are reported either as the average rate over a period of time or as the instantaneous rate at a single time.
The rate law for a reaction is a mathematical relationship between the reaction rate and the concentrations of species in solution. Rate laws can be expressed either as a differential rate law, describing the change in reactant or product concentrations as a function of time, or as an integrated rate law, describing the actual concentrations of reactants or products as a function of time.
The rate constant (k) of a rate law is a constant of proportionality between the reaction rate and the reactant concentration. The power to which a concentration is raised in a rate law indicates the reaction order, the degree to which the reaction rate depends on the concentration of a particular reactant.
Key Takeaways
- Reaction rates can be determined over particular time intervals or at a given point in time.
- A rate law describes the relationship between reactant rates and reactant concentrations.
Key Equations
general definition of rate for A → B
general form of rate law when A and B are reactants
Conceptual Problems
-
Explain why the reaction rate is generally fastest at early time intervals. For the second-order A + B → C, what would the plot of the concentration of C versus time look like during the course of the reaction?
-
Explain the differences between a differential rate law and an integrated rate law. What two components do they have in common? Which form is preferred for obtaining a reaction order and a rate constant? Why?
-
Diffusion-controlled reactions have rates that are determined only by the reaction rate at which two reactant molecules can diffuse together. These reactions are rapid, with second-order rate constants typically on the order of 1010 L/(mol·s). Would you expect the reactions to be faster or slower in solvents that have a low viscosity? Why? Consider the reactions H3O+ + OH− → 2H2O and H3O+ + N(CH3)3 → H2O + HN(CH3)3+ in aqueous solution. Which would have the higher rate constant? Why?
-
What information can you get from the reaction order? What correlation does the reaction order have with the stoichiometry of the overall equation?
-
During the hydrolysis reaction A + H2O → B + C, the concentration of A decreases much more rapidly in a polar solvent than in a nonpolar solvent. How do you expect this effect to be reflected in the overall reaction order?
Answers
-
Reactant concentrations are highest at the beginning of a reaction. The plot of [C] versus t is a curve with a slope that becomes steadily less positive.
-
-
Faster in a less viscous solvent because the rate of diffusion is higher; the H3O+/OH− reaction is faster due to the decreased relative size of reactants and the higher electrostatic attraction between the reactants.
-
-
Numerical Problems
-
The reaction rate of a particular reaction in which A and B react to make C is as follows:
Write a reaction equation that is consistent with this rate law. What is the rate expression with respect to time if 2A are converted to 3C?
-
While commuting to work, a person drove for 12 min at 35 mph, then stopped at an intersection for 2 min, continued the commute at 50 mph for 28 min, drove slowly through traffic at 38 mph for 18 min, and then spent 1 min pulling into a parking space at 3 mph. What was the average rate of the commute? What was the instantaneous rate at 13 min? at 28 min?
-
Why do most studies of chemical reactions use the initial rates of reaction to generate a rate law? How is this initial rate determined? Given the following data, what is the reaction order? Estimate.
Time (s) [A] (M) 120 0.158 240 0.089 360 0.062 -
Predict how the reaction rate will be affected by doubling the concentration of the first species in each equation.
- C2H5I → C2H4 + HI: rate = k[C2H5I]
- SO + O2 → SO2 + O: rate = k[SO][O2]
- 2CH3 → C2H6: rate = k[CH3]2
- ClOO → Cl + O2: rate = k
-
Cleavage of C2H6 to produce two CH3· radicals is a gas-phase reaction that occurs at 700°C. This reaction is first order, with k = 5.46 × 10−4 s−1. How long will it take for the reaction to go to 15% completion? to 50% completion?
-
Three chemical processes occur at an altitude of approximately 100 km in Earth’s atmosphere.
Write a rate law for each elementary reaction. If the rate law for the overall reaction were found to be rate = k[N2+][O2], which one of the steps is rate limiting?
-
The oxidation of aqueous iodide by arsenic acid to give I3− and arsenous acid proceeds via the following reaction:
Write an expression for the initial rate of decrease of [I3−], Δ[I3−]/Δt. When the reaction rate of the forward reaction is equal to that of the reverse reaction: kf/kr = [H3AsO3][I3−]/[H3AsO4][I−]3[H+]2. Based on this information, what can you say about the nature of the rate-determining steps for the reverse and the forward reactions?
Answer
-
-
-
-
-
298 s; 1270 s
-
-
14.3 Methods of Determining Reaction Order
Learning Objective
- To know how to determine the reaction order from experimental data.
In the examples in this text, the exponents in the rate law are almost always the positive integers: 1 and 2 or even 0. Thus the reactions are zeroth, first, or second order in each reactant. The common patterns used to identify the reaction order are described in this section, where we focus on characteristic types of differential and integrated rate laws and how to determine the reaction order from experimental data.
Zeroth-Order Reactions
A zeroth-order reactionA reaction whose rate is independent of concentration. is one whose rate is independent of concentration; its differential rate law is rate = k. We refer to these reactions as zeroth order because we could also write their rate in a form such that the exponent of the reactant in the rate law is 0:
Equation 14.15
Because rate is independent of reactant concentration, a graph of the concentration of any reactant as a function of time is a straight line with a slope of −k. The value of k is negative because the concentration of the reactant decreases with time. Conversely, a graph of the concentration of any product as a function of time is a straight line with a slope of k, a positive value.
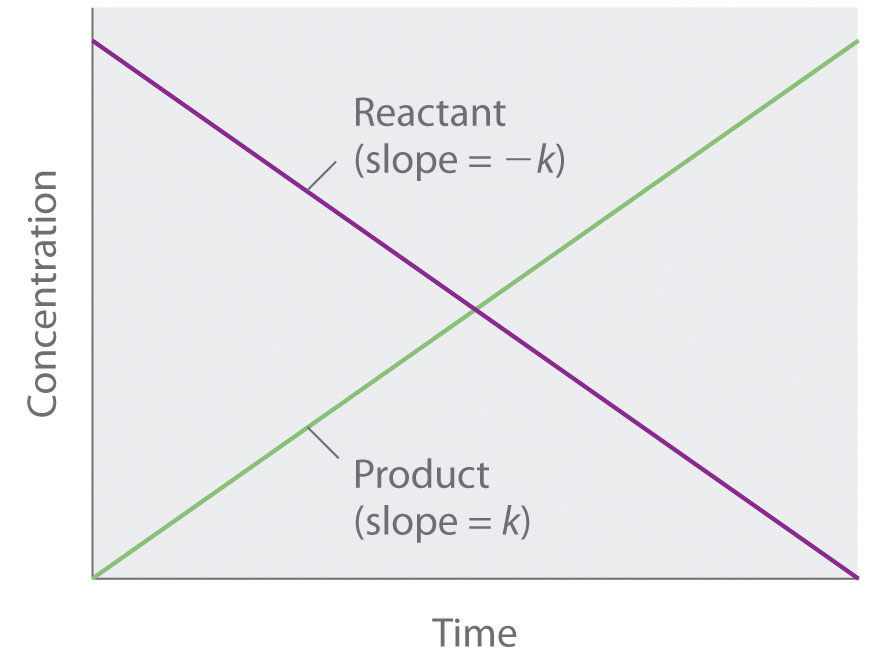
The graph of a zeroth-order reaction. The change in concentration of reactant and product with time produces a straight line.
The integrated rate law for a zeroth-order reaction also produces a straight line and has the general form
Equation 14.16
[A] = [A]0 − ktwhere [A]0 is the initial concentration of reactant A. (Equation 14.16 has the form of the algebraic equation for a straight line, y = mx + b, with y = [A], mx = −kt, and b = [A]0.) In a zeroth-order reaction, the rate constant must have the same units as the reaction rate, typically moles per liter per second.
Although it may seem counterintuitive for the reaction rate to be independent of the reactant concentration(s), such reactions are rather common. They occur most often when the reaction rate is determined by available surface area. An example is the decomposition of N2O on a platinum (Pt) surface to produce N2 and O2, which occurs at temperatures ranging from 200°C to 400°C:
Equation 14.17
Without a platinum surface, the reaction requires temperatures greater than 700°C, but between 200°C and 400°C, the only factor that determines how rapidly N2O decomposes is the amount of Pt surface available (not the amount of Pt). As long as there is enough N2O to react with the entire Pt surface, doubling or quadrupling the N2O concentration will have no effect on the reaction rate.At very low concentrations of N2O, where there are not enough molecules present to occupy the entire available Pt surface, the reaction rate is dependent on the N2O concentration. The reaction rate is as follows:
Equation 14.18
Thus the rate at which N2O is consumed and the rates at which N2 and O2 are produced are independent of concentration. As shown in Figure 14.8 "A Zeroth-Order Reaction", the change in the concentrations of all species with time is linear. Most important, the exponent (0) corresponding to the N2O concentration in the experimentally derived rate law is not the same as the reactant’s stoichiometric coefficient in the balanced chemical equation (2). For this reaction, as for all others, the rate law must be determined experimentally.
Figure 14.8 A Zeroth-Order Reaction
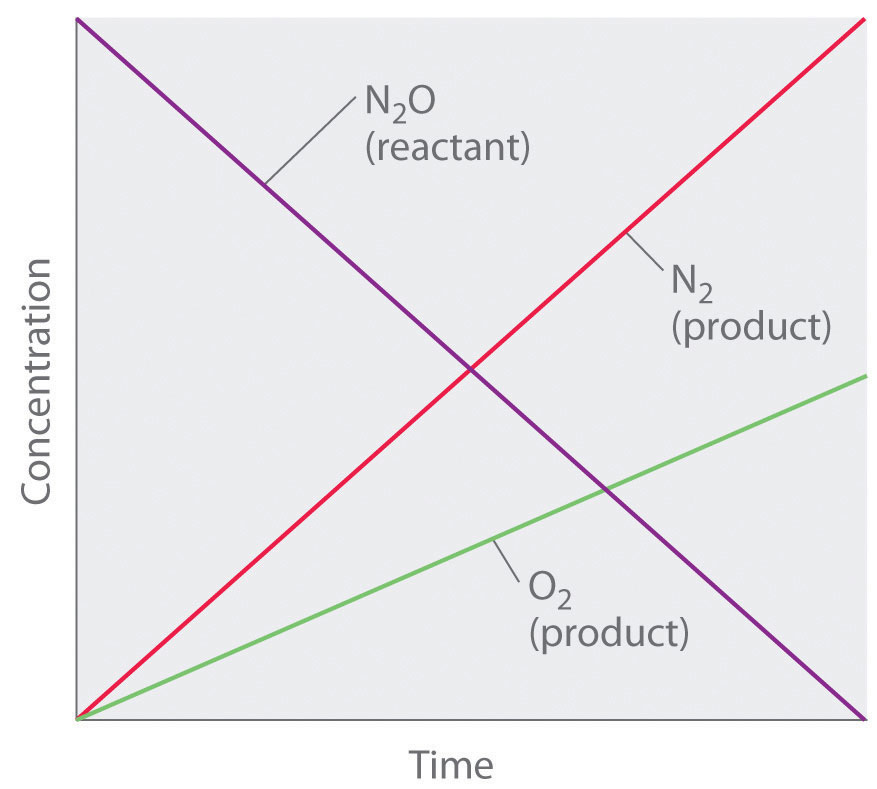
This graph shows the concentrations of reactants and products versus time for the zeroth-order catalyzed decomposition of N2O to N2 and O2 on a Pt surface. The change in the concentrations of all species with time is linear.
Note the Pattern
If a plot of reactant concentration versus time is linear, then the reaction is zeroth order in that reactant.
A zeroth-order reaction that takes place in the human liver is the oxidation of ethanol (from alcoholic beverages) to acetaldehyde, catalyzed by the enzymeA catalyst that occurs naturally in living organisms and catalyzes biological reactions. alcohol dehydrogenase. At high ethanol concentrations, this reaction is also a zeroth-order reaction. The overall reaction equation is
Figure 14.9

where NAD+ (nicotinamide adenine dinucleotide) and NADH (reduced nicotinamide adenine dinucleotide) are the oxidized and reduced forms, respectively, of a species used by all organisms to transport electrons. When an alcoholic beverage is consumed, the ethanol is rapidly absorbed into the blood. Its concentration then decreases at a constant rate until it reaches zero (part (a) in Figure 14.10 "The Catalyzed Oxidation of Ethanol"). An average 70 kg person typically takes about 2.5 h to oxidize the 15 mL of ethanol contained in a single 12 oz can of beer, a 5 oz glass of wine, or a shot of distilled spirits (such as whiskey or brandy). The actual rate, however, varies a great deal from person to person, depending on body size and the amount of alcohol dehydrogenase in the liver. The reaction rate does not increase if a greater quantity of alcohol is consumed over the same period of time because the reaction rate is determined only by the amount of enzyme present in the liver.Contrary to popular belief, the caffeine in coffee is ineffective at catalyzing the oxidation of ethanol. When the ethanol has been completely oxidized and its concentration drops to essentially zero, the rate of oxidation also drops rapidly (part (b) in Figure 14.10 "The Catalyzed Oxidation of Ethanol").
Figure 14.10 The Catalyzed Oxidation of Ethanol
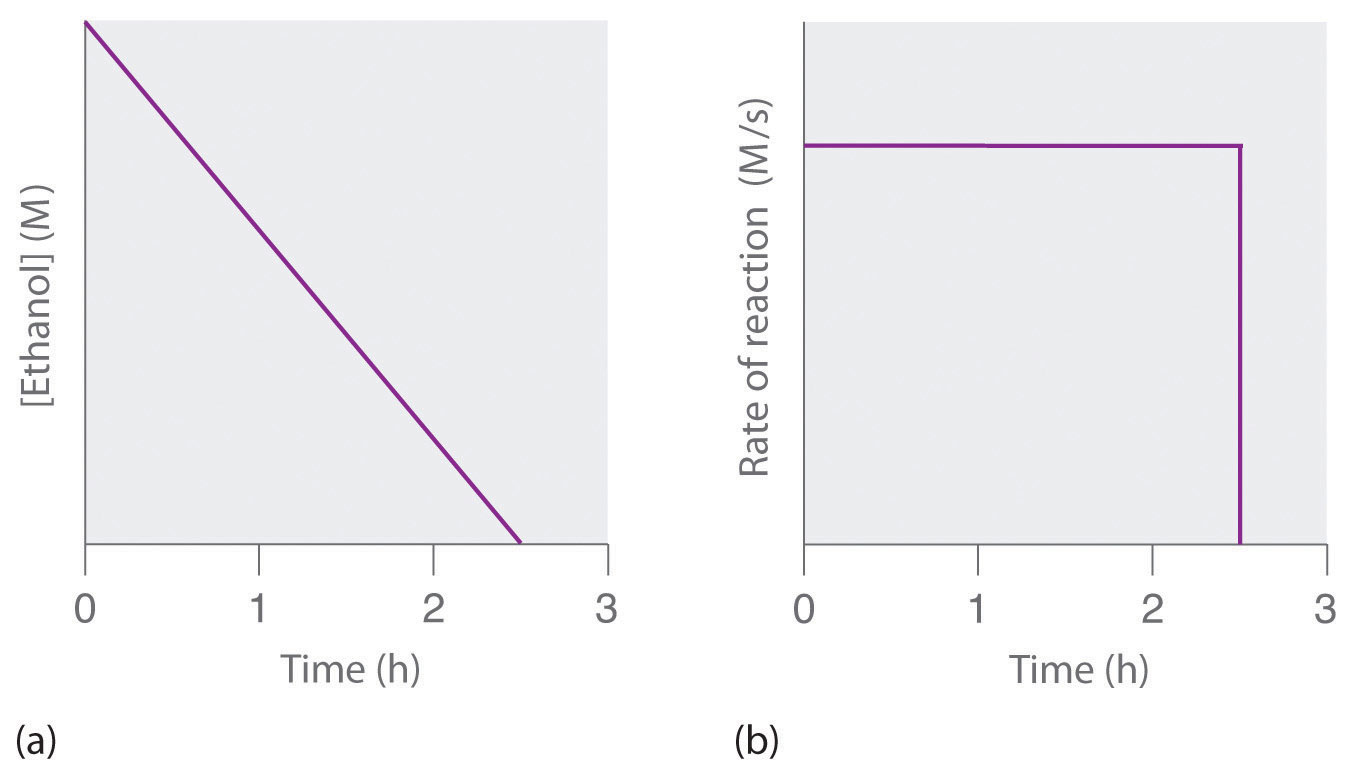
(a) The concentration of ethanol in human blood decreases linearly with time, which is typical of a zeroth-order reaction. (b) The rate at which ethanol is oxidized is constant until the ethanol concentration reaches essentially zero, at which point the reaction rate drops to zero.
These examples illustrate two important points:
- In a zeroth-order reaction, the reaction rate does not depend on the reactant concentration.
- A linear change in concentration with time is a clear indication of a zeroth-order reaction.
First-Order Reactions
In a first-order reactionA reaction whose rate is directly proportional to the concentration of one reactant., the reaction rate is directly proportional to the concentration of one of the reactants. First-order reactions often have the general form A → products. The differential rate for a first-order reaction is as follows:
Equation 14.19
If the concentration of A is doubled, the reaction rate doubles; if the concentration of A is increased by a factor of 10, the reaction rate increases by a factor of 10, and so forth. Because the units of the reaction rate are always moles per liter per second, the units of a first-order rate constant are reciprocal seconds (s−1).
The integrated rate law for a first-order reaction can be written in two different ways: one using exponents and one using logarithms. The exponential form is as follows:
Equation 14.20
[A] = [A]0e−ktwhere [A]0 is the initial concentration of reactant A at t = 0; k is the rate constant; and e is the base of the natural logarithms, which has the value 2.718 to three decimal places. (Essential Skills 6 in Chapter 11 "Liquids", Section 11.9 "Essential Skills 6", discusses natural logarithms.) Recall that an integrated rate law gives the relationship between reactant concentration and time. Equation 14.20 predicts that the concentration of A will decrease in a smooth exponential curve over time. By taking the natural logarithm of each side of Equation 14.20 and rearranging, we obtain an alternative logarithmic expression of the relationship between the concentration of A and t:
Equation 14.21
ln[A] = ln[A]0 − ktBecause Equation 14.21 has the form of the algebraic equation for a straight line, y = mx + b, with y = ln[A] and b = ln[A]0, a plot of ln[A] versus t for a first-order reaction should give a straight line with a slope of −k and an intercept of ln[A]0. Either the differential rate law (Equation 14.19) or the integrated rate law (Equation 14.21) can be used to determine whether a particular reaction is first order.
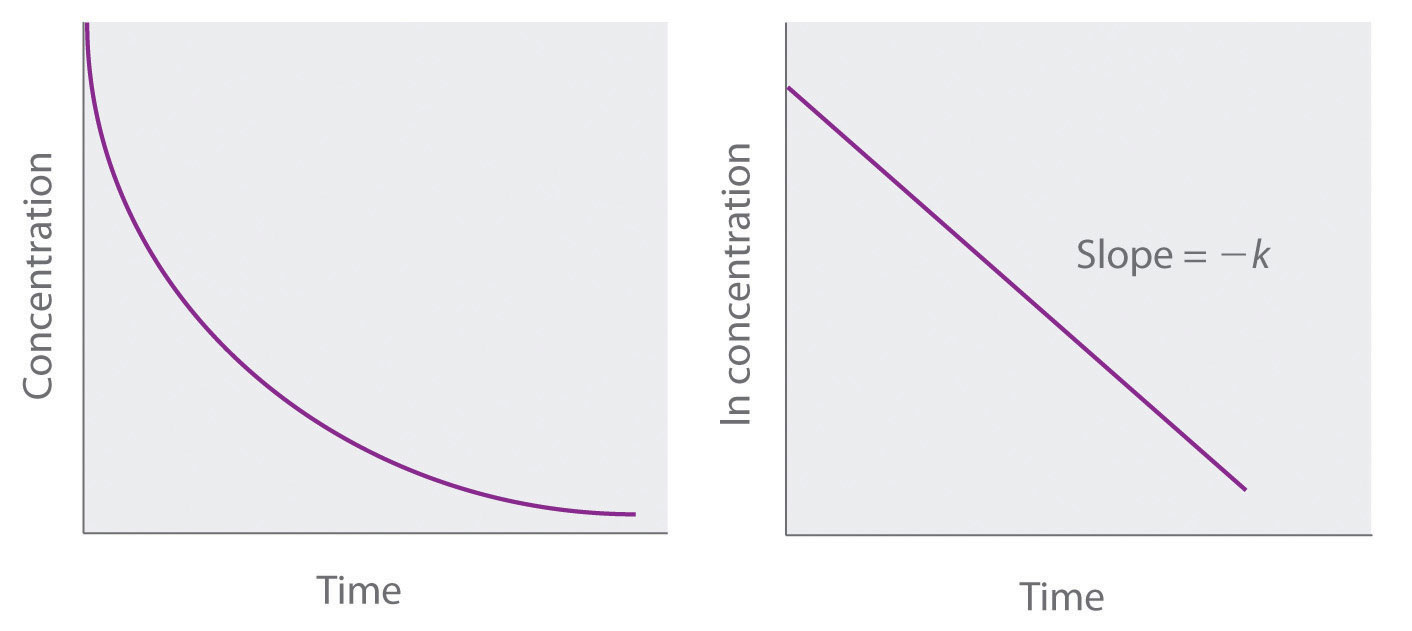
Graphs of a first-order reaction. The expected shapes of the curves for plots of reactant concentration versus time (top) and the natural logarithm of reactant concentration versus time (bottom) for a first-order reaction.
First-order reactions are very common. In this chapter, we have already encountered two examples of first-order reactions: the hydrolysis of aspirin (Figure 14.6) and the reaction of t-butyl bromide with water to give t-butanol (Equation 14.10). Another reaction that exhibits apparent first-order kinetics is the hydrolysis of the anticancer drug cisplatin.
Cisplatin, the first “inorganic” anticancer drug to be discovered, is unique in its ability to cause complete remission of the relatively rare but deadly cancers of the reproductive organs in young adults. The structures of cisplatin and its hydrolysis product are as follows:
Figure 14.11
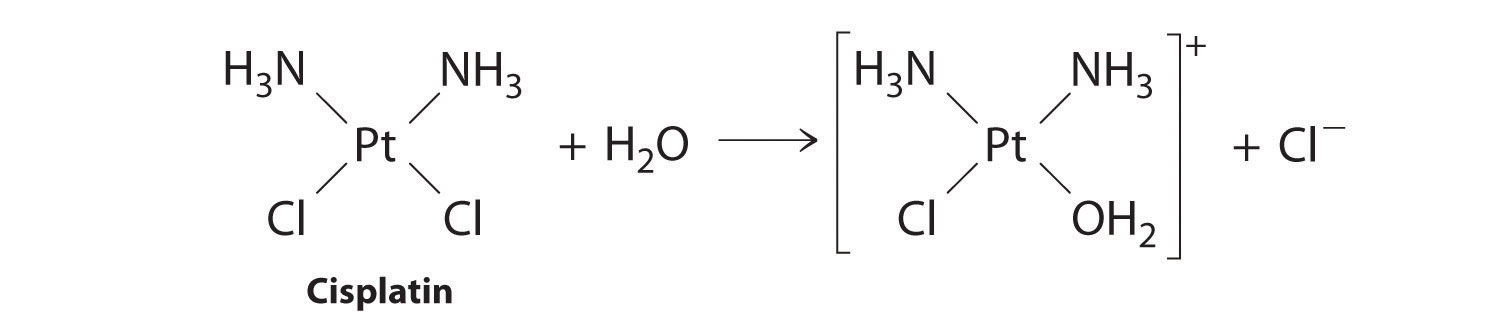
Both platinum compounds have four groups arranged in a square plane around a Pt(II) ion. The reaction shown in Figure 14.11 is important because cisplatin, the form in which the drug is administered, is not the form in which the drug is active. Instead, at least one chloride ion must be replaced by water to produce a species that reacts with deoxyribonucleic acid (DNA) to prevent cell division and tumor growth. Consequently, the kinetics of the reaction in Figure 14.11 have been studied extensively to find ways of maximizing the concentration of the active species.
Note the Pattern
If a plot of reactant concentration versus time is not linear but a plot of the natural logarithm of reactant concentration versus time is linear, then the reaction is first order.
The rate law and reaction order of the hydrolysis of cisplatin are determined from experimental data, such as those displayed in Table 14.2 "Rates of Hydrolysis of Cisplatin as a Function of Concentration at pH 7.0 and 25°C". The table lists initial rate data for four experiments in which the reaction was run at pH 7.0 and 25°C but with different initial concentrations of cisplatin. Because the reaction rate increases with increasing cisplatin concentration, we know this cannot be a zeroth-order reaction. Comparing Experiments 1 and 2 in Table 14.2 "Rates of Hydrolysis of Cisplatin as a Function of Concentration at pH 7.0 and 25°C" shows that the reaction rate doubles [(1.8 × 10−5 M/min) ÷ (9.0 × 10−6 M/min) = 2.0] when the concentration of cisplatin is doubled (from 0.0060 M to 0.012 M). Similarly, comparing Experiments 1 and 4 shows that the reaction rate increases by a factor of 5 [(4.5 × 10−5 M/min) ÷ (9.0 × 10−6 M/min) = 5.0] when the concentration of cisplatin is increased by a factor of 5 (from 0.0060 M to 0.030 M). Because the reaction rate is directly proportional to the concentration of the reactant, the exponent of the cisplatin concentration in the rate law must be 1, so the rate law is rate = k[cisplatin]1. Thus the reaction is first order. Knowing this, we can calculate the rate constant using the differential rate law for a first-order reaction and the data in any row of Table 14.2 "Rates of Hydrolysis of Cisplatin as a Function of Concentration at pH 7.0 and 25°C". For example, substituting the values for Experiment 3 into Equation 14.19,
3.6 × 10−5 M/min = k(0.024 M) 1.5 × 10−3 min−1 = kTable 14.2 Rates of Hydrolysis of Cisplatin as a Function of Concentration at pH 7.0 and 25°C
| Experiment | [Cisplatin]0 (M) | Initial Rate (M/min) |
|---|---|---|
| 1 | 0.0060 | 9.0 × 10−6 |
| 2 | 0.012 | 1.8 × 10−5 |
| 3 | 0.024 | 3.6 × 10−5 |
| 4 | 0.030 | 4.5 × 10−5 |
Knowing the rate constant for the hydrolysis of cisplatin and the rate constants for subsequent reactions that produce species that are highly toxic enables hospital pharmacists to provide patients with solutions that contain only the desired form of the drug.
Example 4
At high temperatures, ethyl chloride produces HCl and ethylene by the following reaction:
Using the rate data for the reaction at 650°C presented in the following table, calculate the reaction order with respect to the concentration of ethyl chloride and determine the rate constant for the reaction.
| Experiment | [CH3CH2Cl]0 (M) | Initial Rate (M/s) |
|---|---|---|
| 1 | 0.010 | 1.6 × 10−8 |
| 2 | 0.015 | 2.4 × 10−8 |
| 3 | 0.030 | 4.8 × 10−8 |
| 4 | 0.040 | 6.4 × 10−8 |
Given: balanced chemical equation, initial concentrations of reactant, and initial rates of reaction
Asked for: reaction order and rate constant
Strategy:
A Compare the data from two experiments to determine the effect on the reaction rate of changing the concentration of a species.
B Compare the observed effect with behaviors characteristic of zeroth- and first-order reactions to determine the reaction order. Write the rate law for the reaction.
C Use measured concentrations and rate data from any of the experiments to find the rate constant.
Solution:
The reaction order with respect to ethyl chloride is determined by examining the effect of changes in the ethyl chloride concentration on the reaction rate.
A Comparing Experiments 2 and 3 shows that doubling the concentration doubles the reaction rate, so the reaction rate is proportional to [CH3CH2Cl]. Similarly, comparing Experiments 1 and 4 shows that quadrupling the concentration quadruples the reaction rate, again indicating that the reaction rate is directly proportional to [CH3CH2Cl].
B This behavior is characteristic of a first-order reaction, for which the rate law is rate = k[CH3CH2Cl].
C We can calculate the rate constant (k) using any row in the table. Selecting Experiment 1 gives the following:
1.60 × 10−8 M/s = k(0.010 M) 1.6 × 10−6 s−1 = kExercise
Sulfuryl chloride (SO2Cl2) decomposes to SO2 and Cl2 by the following reaction:
SO2Cl2(g) → SO2(g) + Cl2(g)Data for the reaction at 320°C are listed in the following table. Calculate the reaction order with regard to sulfuryl chloride and determine the rate constant for the reaction.
| Experiment | [SO2Cl2]0 (M) | Initial Rate (M/s) |
|---|---|---|
| 1 | 0.0050 | 1.10 × 10−7 |
| 2 | 0.0075 | 1.65 × 10−7 |
| 3 | 0.0100 | 2.20 × 10−7 |
| 4 | 0.0125 | 2.75 × 10−7 |
Answer: first order; k = 2.2 × 10−5 s−1
Figure 14.12 The Hydrolysis of Cisplatin, a First-Order Reaction
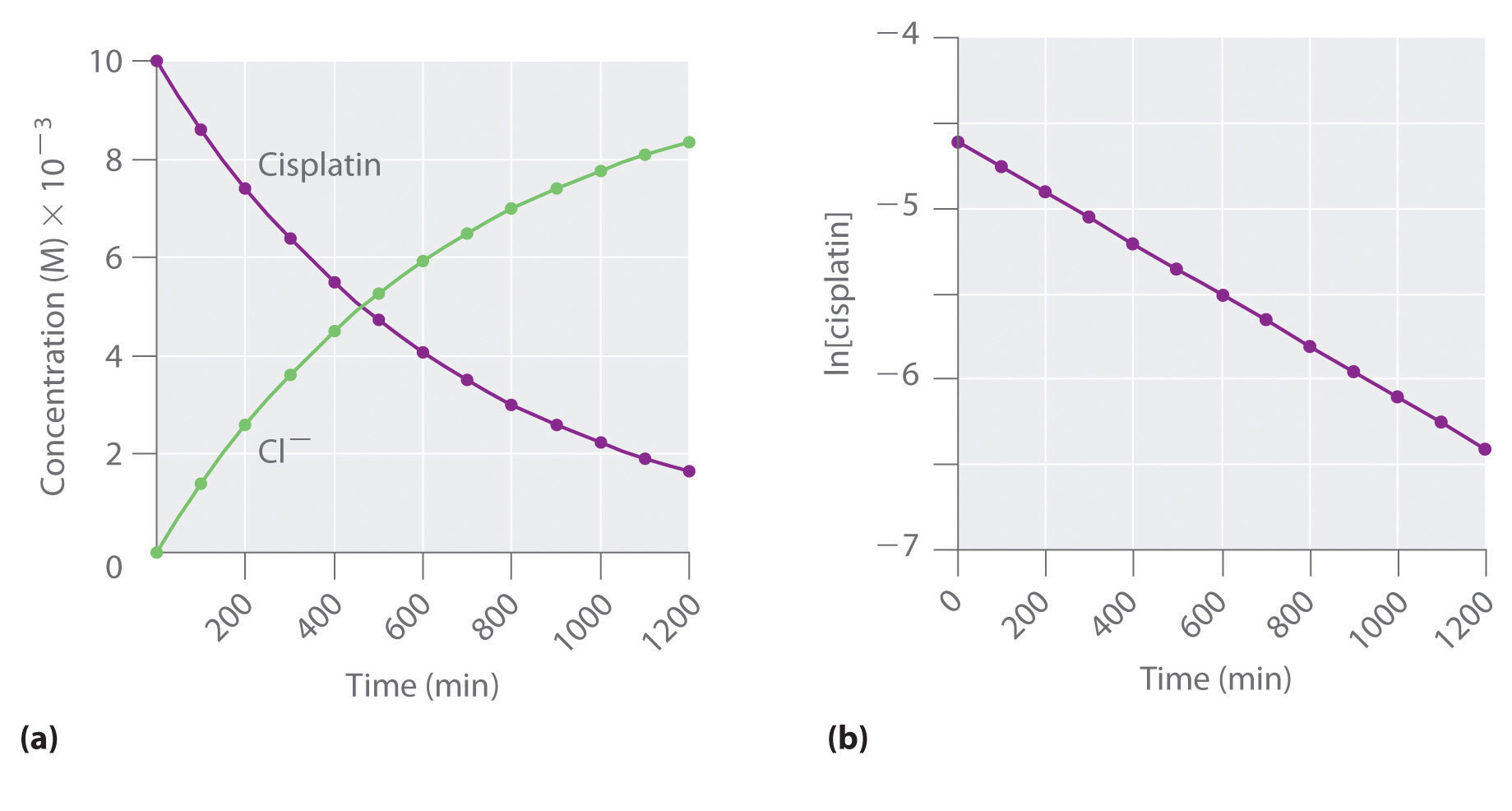
These plots show hydrolysis of cisplatin at pH 7.0 and 25°C as (a) the experimentally determined concentrations of cisplatin and chloride ions versus time and (b) the natural logarithm of the cisplatin concentration versus time. The straight line in (b) is expected for a first-order reaction.
We can also use the integrated rate law to determine the reaction rate for the hydrolysis of cisplatin. To do this, we examine the change in the concentration of the reactant or the product as a function of time at a single initial cisplatin concentration. Part (a) in Figure 14.12 "The Hydrolysis of Cisplatin, a First-Order Reaction" shows plots for a solution that originally contained 0.0100 M cisplatin and was maintained at pH 7 and 25°C. The concentration of cisplatin decreases smoothly with time, and the concentration of chloride ion increases in a similar way. When we plot the natural logarithm of the concentration of cisplatin versus time, we obtain the plot shown in part (b) in Figure 14.12 "The Hydrolysis of Cisplatin, a First-Order Reaction". The straight line is consistent with the behavior of a system that obeys a first-order rate law. We can use any two points on the line to calculate the slope of the line, which gives us the rate constant for the reaction. Thus taking the points from part (a) in Figure 14.12 "The Hydrolysis of Cisplatin, a First-Order Reaction" for t = 100 min ([cisplatin] = 0.0086 M) and t = 1000 min ([cisplatin] = 0.0022 M),
The slope is negative because we are calculating the rate of disappearance of cisplatin. Also, the rate constant has units of min−1 because the times plotted on the horizontal axes in parts (a) and (b) in Figure 14.12 "The Hydrolysis of Cisplatin, a First-Order Reaction" are in minutes rather than seconds.
The reaction order and the magnitude of the rate constant we obtain using the integrated rate law are exactly the same as those we calculated earlier using the differential rate law. This must be true if the experiments were carried out under the same conditions.
Example 5
Refer back to Example 4. If a sample of ethyl chloride with an initial concentration of 0.0200 M is heated at 650°C, what is the concentration of ethyl chloride after 10 h? How many hours at 650°C must elapse for the concentration to decrease to 0.0050 M? (Recall that we calculated the rate constant for this reaction in Example 4.)
Given: initial concentration, rate constant, and time interval
Asked for: concentration at specified time and time required to obtain particular concentration
Strategy:
A Substitute values for the initial concentration ([A]0) and the calculated rate constant for the reaction (k) into the integrated rate law for a first-order reaction. Calculate the concentration ([A]) at the given time t.
B Given a concentration [A], solve the integrated rate law for time t.
Solution:
The exponential form of the integrated rate law for a first-order reaction (Equation 14.20) is [A] = [A]0e−kt.
A Having been given the initial concentration of ethyl chloride ([A]0) and having calculated the rate constant in Example 4 (k = 1.6 × 10−6 s−1), we can use the rate law to calculate the concentration of the reactant at a given time t. Substituting the known values into the integrated rate law,
We could also have used the logarithmic form of the integrated rate law (Equation 14.21):
B To calculate the amount of time required to reach a given concentration, we must solve the integrated rate law for t. Equation 14.21 gives the following:
Exercise
In the exercise in Example 4, you found that the decomposition of sulfuryl chloride (SO2Cl2) is first order, and you calculated the rate constant at 320°C. Use the form(s) of the integrated rate law to find the amount of SO2Cl2 that remains after 20 h if a sample with an original concentration of 0.123 M is heated at 320°C. How long would it take for 90% of the SO2Cl2 to decompose?
Answer: 0.0252 M; 29 h
Second-Order Reactions
The simplest kind of second-order reactionA reaction whose rate is proportional to the square of the concentration of the reactant (for a reaction with the general form 2A → products) or is proportional to the product of the concentrations of two reactants (for a reaction with the general form A + B → products). is one whose rate is proportional to the square of the concentration of one reactant. These generally have the form 2A → products. A second kind of second-order reaction has a reaction rate that is proportional to the product of the concentrations of two reactants. Such reactions generally have the form A + B → products. An example of the former is a dimerization reaction, in which two smaller molecules, each called a monomer, combine to form a larger molecule (a dimer).
The differential rate law for the simplest second-order reaction in which 2A → products is as follows:
Equation 14.22
Consequently, doubling the concentration of A quadruples the reaction rate. For the units of the reaction rate to be moles per liter per second (M/s), the units of a second-order rate constant must be the inverse (M−1·s−1). Because the units of molarity are expressed as mol/L, the unit of the rate constant can also be written as L(mol·s).
For the reaction 2A → products, the following integrated rate law describes the concentration of the reactant at a given time:
Equation 14.23
Because Equation 14.23 has the form of an algebraic equation for a straight line, y = mx + b, with y = 1/[A] and b = 1/[A]0, a plot of 1/[A] versus t for a simple second-order reaction is a straight line with a slope of k and an intercept of 1/[A]0.
Note the Pattern
Second-order reactions generally have the form 2A → products or A + B → products.
Simple second-order reactions are common. In addition to dimerization reactions, two other examples are the decomposition of NO2 to NO and O2 and the decomposition of HI to I2 and H2. Most examples involve simple inorganic molecules, but there are organic examples as well. We can follow the progress of the reaction described in the following paragraph by monitoring the decrease in the intensity of the red color of the reaction mixture.
Many cyclic organic compounds that contain two carbon–carbon double bonds undergo a dimerization reaction to give complex structures. One example is as follows:
Figure 14.13
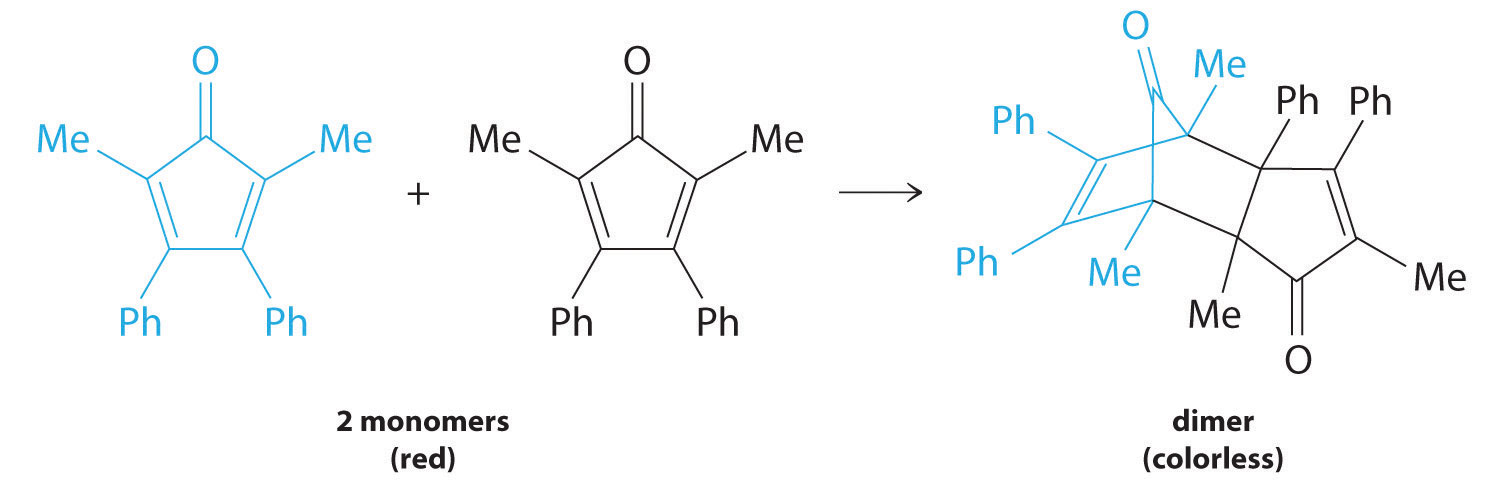
For simplicity, we will refer to this reactant and product as “monomer” and “dimer,” respectively.The systematic name of the monomer is 2,5-dimethyl-3,4-diphenylcyclopentadienone. The systematic name of the dimer is the name of the monomer followed by “dimer.” Because the monomers are the same, the general equation for this reaction is 2A → product. This reaction represents an important class of organic reactions used in the pharmaceutical industry to prepare complex carbon skeletons for the synthesis of drugs. Like the first-order reactions studied previously, it can be analyzed using either the differential rate law (Equation 14.22) or the integrated rate law (Equation 14.23).
To determine the differential rate law for the reaction, we need data on how the reaction rate varies as a function of monomer concentrations, which are provided in Table 14.3 "Rates of Reaction as a Function of Monomer Concentration for an Initial Monomer Concentration of 0.0054 M". From the data, we see that the reaction rate is not independent of the monomer concentration, so this is not a zeroth-order reaction. We also see that the reaction rate is not proportional to the monomer concentration, so the reaction is not first order. Comparing the data in the second and fourth rows shows that the reaction rate decreases by a factor of 2.8 when the monomer concentration decreases by a factor of 1.7:
Table 14.3 Rates of Reaction as a Function of Monomer Concentration for an Initial Monomer Concentration of 0.0054 M
| Time (min) | [Monomer] (M) | Instantaneous Rate (M/min) |
|---|---|---|
| 10 | 0.0044 | 8.0 × 10−5 |
| 26 | 0.0034 | 5.0 × 10−5 |
| 44 | 0.0027 | 3.1 × 10−5 |
| 70 | 0.0020 | 1.8 × 10−5 |
| 120 | 0.0014 | 8.0 × 10−6 |
Because (1.7)2 = 2.9 ≈ 2.8, the reaction rate is approximately proportional to the square of the monomer concentration.
rate ∝ [monomer]2This means that the reaction is second order in the monomer. Using Equation 14.22 and the data from any row in Table 14.3 "Rates of Reaction as a Function of Monomer Concentration for an Initial Monomer Concentration of 0.0054 M", we can calculate the rate constant. Substituting values at time 10 min, for example, gives the following:
We can also determine the reaction order using the integrated rate law. To do so, we use the decrease in the concentration of the monomer as a function of time for a single reaction, plotted in part (a) in Figure 14.14 "Dimerization of a Monomeric Compound, a Second-Order Reaction". The measurements show that the concentration of the monomer (initially 5.4 × 10−3 M) decreases with increasing time. This graph also shows that the reaction rate decreases smoothly with increasing time. According to the integrated rate law for a second-order reaction, a plot of 1/[monomer] versus t should be a straight line, as shown in part (b) in Figure 14.14 "Dimerization of a Monomeric Compound, a Second-Order Reaction". Any pair of points on the line can be used to calculate the slope, which is the second-order rate constant. In this example, k = 4.1 M−1·min−1, which is consistent with the result obtained using the differential rate equation. Although in this example the stoichiometric coefficient is the same as the reaction order, this is not always the case. The reaction order must always be determined experimentally.
Figure 14.14 Dimerization of a Monomeric Compound, a Second-Order Reaction
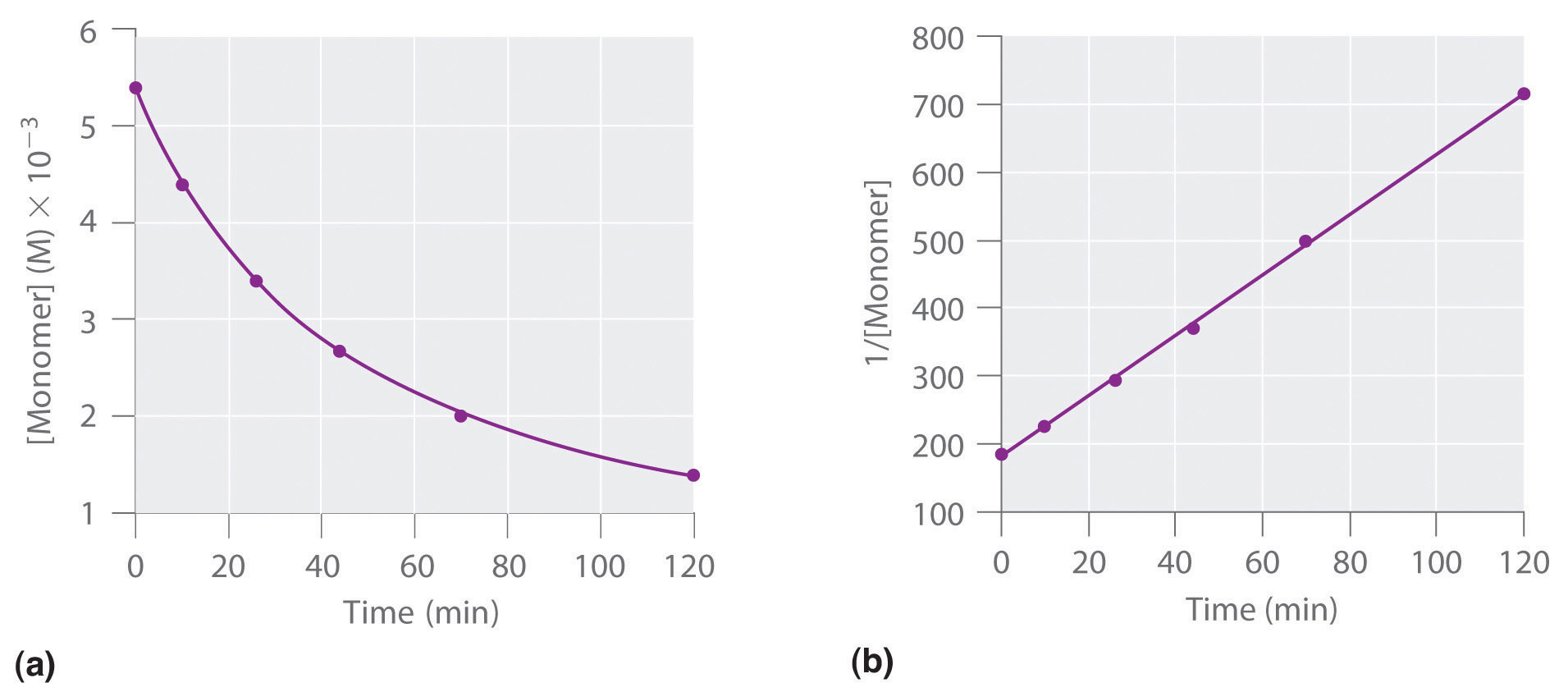
These plots correspond to dimerization of the monomer in Figure 14.13 " " as (a) the experimentally determined concentration of monomer versus time and (b) 1/[monomer] versus time. The straight line in (b) is expected for a simple second-order reaction.
For two or more reactions of the same order, the reaction with the largest rate constant is the fastest. Because the units of the rate constants for zeroth-, first-, and second-order reactions are different, however, we cannot compare the magnitudes of rate constants for reactions that have different orders. The differential and integrated rate laws for zeroth-, first-, and second-order reactions and their corresponding graphs are shown in Figure 14.16 "Properties of Reactions That Obey Zeroth-, First-, and Second-Order Rate Laws" in Section 14.4 "Using Graphs to Determine Rate Laws, Rate Constants, and Reaction Orders".
Example 6
At high temperatures, nitrogen dioxide decomposes to nitric oxide and oxygen.
Experimental data for the reaction at 300°C and four initial concentrations of NO2 are listed in the following table:
| Experiment | [NO2]0 (M) | Initial Rate (M/s) |
|---|---|---|
| 1 | 0.015 | 1.22 × 10−4 |
| 2 | 0.010 | 5.40 × 10−5 |
| 3 | 0.0080 | 3.46 × 10−5 |
| 4 | 0.0050 | 1.35 × 10−5 |
Determine the reaction order and the rate constant.
Given: balanced chemical equation, initial concentrations, and initial rates
Asked for: reaction order and rate constant
Strategy:
A From the experiments, compare the changes in the initial reaction rates with the corresponding changes in the initial concentrations. Determine whether the changes are characteristic of zeroth-, first-, or second-order reactions.
B Determine the appropriate rate law. Using this rate law and data from any experiment, solve for the rate constant (k).
Solution:
A We can determine the reaction order with respect to nitrogen dioxide by comparing the changes in NO2 concentrations with the corresponding reaction rates. Comparing Experiments 2 and 4, for example, shows that doubling the concentration quadruples the reaction rate [(5.40 × 10−5) ÷ (1.35 × 10−5) = 4.0], which means that the reaction rate is proportional to [NO2]2. Similarly, comparing Experiments 1 and 4 shows that tripling the concentration increases the reaction rate by a factor of 9, again indicating that the reaction rate is proportional to [NO2]2. This behavior is characteristic of a second-order reaction.
B We have rate = k[NO2]2. We can calculate the rate constant (k) using data from any experiment in the table. Selecting Experiment 2, for example, gives the following:
Exercise
When the highly reactive species HO2 forms in the atmosphere, one important reaction that then removes it from the atmosphere is as follows:
2HO2(g) → H2O2(g) + O2(g)The kinetics of this reaction have been studied in the laboratory, and some initial rate data at 25°C are listed in the following table:
| Experiment | [HO2]0 (M) | Initial Rate (M/s) |
|---|---|---|
| 1 | 1.1 × 10−8 | 1.7 × 10−7 |
| 2 | 2.5 × 10−8 | 8.8 × 10−7 |
| 3 | 3.4 × 10−8 | 1.6 × 10−6 |
| 4 | 5.0 × 10−8 | 3.5 × 10−6 |
Determine the reaction order and the rate constant.
Answer: second order in HO2; k = 1.4 × 109 M−1·s−1
Note the Pattern
If a plot of reactant concentration versus time is not linear but a plot of 1/reaction concentration versus time is linear, then the reaction is second order.
Example 7
If a flask that initially contains 0.056 M NO2 is heated at 300°C, what will be the concentration of NO2 after 1.0 h? How long will it take for the concentration of NO2 to decrease to 10% of the initial concentration? Use the integrated rate law for a second-order reaction (Equation 14.23) and the rate constant calculated in Example 6.
Given: balanced chemical equation, rate constant, time interval, and initial concentration
Asked for: final concentration and time required to reach specified concentration
Strategy:
A Given k, t, and [A]0, use the integrated rate law for a second-order reaction to calculate [A].
B Setting [A] equal to 1/10 of [A]0, use the same equation to solve for t.
Solution:
A We know k and [NO2]0, and we are asked to determine [NO2] at t = 1 h (3600 s). Substituting the appropriate values into Equation 14.23,
Thus [NO2]3600 = 5.1 × 10−4 M.
B In this case, we know k and [NO2]0, and we are asked to calculate at what time [NO2] = 0.1[NO2]0 = 0.1(0.056 M) = 0.0056 M. To do this, we solve Equation 14.23 for t, using the concentrations given.
NO2 decomposes very rapidly; under these conditions, the reaction is 90% complete in only 5.0 min.
Exercise
In the exercise in Example 6, you calculated the rate constant for the decomposition of HO2 as k = 1.4 × 109 M−1·s−1. This high rate constant means that HO2 decomposes rapidly under the reaction conditions given in the problem. In fact, the HO2 molecule is so reactive that it is virtually impossible to obtain in high concentrations. Given a 0.0010 M sample of HO2, calculate the concentration of HO2 that remains after 1.0 h at 25°C. How long will it take for 90% of the HO2 to decompose? Use the integrated rate law for a second-order reaction (Equation 14.23) and the rate constant calculated in the exercise in Example 6.
Answer: 2.0 × 10−13 M; 6.4 × 10−6 s
In addition to the simple second-order reaction and rate law we have just described, another very common second-order reaction has the general form A + B → products, in which the reaction is first order in A and first order in B. The differential rate law for this reaction is as follows:
Equation 14.24
Because the reaction is first order both in A and in B, it has an overall reaction order of 2. (The integrated rate law for this reaction is rather complex, so we will not describe it.) We can recognize second-order reactions of this sort because the reaction rate is proportional to the concentrations of each reactant. We presented one example at the end of Section 14.2 "Reaction Rates and Rate Laws", the reaction of CH3Br with OH− to produce CH3OH.
Determining the Rate Law of a Reaction
The number of fundamentally different mechanisms (sets of steps in a reaction) is actually rather small compared to the large number of chemical reactions that can occur. Thus understanding reaction mechanismsThe sequence of events that occur at the molecular level during a reaction. can simplify what might seem to be a confusing variety of chemical reactions. The first step in discovering the reaction mechanism is to determine the reaction’s rate law. This can be done by designing experiments that measure the concentration(s) of one or more reactants or products as a function of time. For the reaction A + B → products, for example, we need to determine k and the exponents m and n in the following equation:
Equation 14.25
rate = k[A]m[B]nTo do this, we might keep the initial concentration of B constant while varying the initial concentration of A and calculating the initial reaction rate. This information would permit us to deduce the reaction order with respect to A. Similarly, we could determine the reaction order with respect to B by studying the initial reaction rate when the initial concentration of A is kept constant while the initial concentration of B is varied. In earlier examples, we determined the reaction order with respect to a given reactant by comparing the different rates obtained when only the concentration of the reactant in question was changed. An alternative way of determining reaction orders is to set up a proportion using the rate laws for two different experiments.
Rate data for a hypothetical reaction of the type A + B → products are given in Table 14.4 "Rate Data for a Hypothetical Reaction of the Form A + B → Products". The general rate law for the reaction is given in Equation 14.25. We can obtain m or n directly by using a proportion of the rate laws for two experiments in which the concentration of one reactant is the same, such as Experiments 1 and 3 in Table 14.4 "Rate Data for a Hypothetical Reaction of the Form A + B → Products".
Table 14.4 Rate Data for a Hypothetical Reaction of the Form A + B → Products
| Experiment | [A] (M) | [B] (M) | Initial Rate (M/min) |
|---|---|---|---|
| 1 | 0.50 | 0.50 | 8.5 × 10−3 |
| 2 | 0.75 | 0.50 | 19 × 10−3 |
| 3 | 1.00 | 0.50 | 34 × 10−3 |
| 4 | 0.50 | 0.75 | 8.5 × 10−3 |
| 5 | 0.50 | 1.00 | 8.5 × 10−3 |
Inserting the appropriate values from Table 14.4 "Rate Data for a Hypothetical Reaction of the Form A + B → Products",
Because 1.00 to any power is 1, [1.00 M]m = 1.00 M. We can cancel like terms to give 0.25 = [0.50]m, which can also be written as 1/4 = [1/2]m. Thus we can conclude that m = 2 and that the reaction is second order in A. By selecting two experiments in which the concentration of B is the same, we were able to solve for m.
Conversely, by selecting two experiments in which the concentration of A is the same (e.g., Experiments 5 and 1), we can solve for n.
Substituting the appropriate values from Table 14.4 "Rate Data for a Hypothetical Reaction of the Form A + B → Products",
Canceling leaves 1.0 = [0.50]n, which gives n = 0; that is, the reaction is zeroth order in B. The experimentally determined rate law is therefore
rate = k[A]2[B]0 = k[A]2We can now calculate the rate constant by inserting the data from any row of Table 14.4 "Rate Data for a Hypothetical Reaction of the Form A + B → Products" into the experimentally determined rate law and solving for k. Using Experiment 2, we obtain
19 × 10−3 M/min = k(0.75 M)2 3.4 × 10−2 M−1·min−1 = kYou should verify that using data from any other row of Table 14.4 "Rate Data for a Hypothetical Reaction of the Form A + B → Products" gives the same rate constant. This must be true as long as the experimental conditions, such as temperature and solvent, are the same.
Example 8
Nitric oxide is produced in the body by several different enzymes and acts as a signal that controls blood pressure, long-term memory, and other critical functions. The major route for removing NO from biological fluids is via reaction with O2 to give NO2, which then reacts rapidly with water to give nitrous acid and nitric acid:

These reactions are important in maintaining steady levels of NO. The following table lists kinetics data for the reaction of NO with O2 at 25°C:
2NO(g) + O2(g) → 2NO2(g)Determine the rate law for the reaction and calculate the rate constant.
| Experiment | [NO]0 (M) | [O2]0 (M) | Initial Rate (M/s) |
|---|---|---|---|
| 1 | 0.0235 | 0.0125 | 7.98 × 10−3 |
| 2 | 0.0235 | 0.0250 | 15.9 × 10−3 |
| 3 | 0.0470 | 0.0125 | 32.0 × 10−3 |
| 4 | 0.0470 | 0.0250 | 63.5 × 10−3 |
Given: balanced chemical equation, initial concentrations, and initial rates
Asked for: rate law and rate constant
Strategy:
A Compare the changes in initial concentrations with the corresponding changes in rates of reaction to determine the reaction order for each species. Write the rate law for the reaction.
B Using data from any experiment, substitute appropriate values into the rate law. Solve the rate equation for k.
Solution:
A Comparing Experiments 1 and 2 shows that as [O2] is doubled at a constant value of [NO2], the reaction rate approximately doubles. Thus the reaction rate is proportional to [O2]1, so the reaction is first order in O2. Comparing Experiments 1 and 3 shows that the reaction rate essentially quadruples when [NO] is doubled and [O2] is held constant. That is, the reaction rate is proportional to [NO]2, which indicates that the reaction is second order in NO. Using these relationships, we can write the rate law for the reaction:
rate = k[NO]2[O2]B The data in any row can be used to calculate the rate constant. Using Experiment 1, for example, gives
The overall reaction order (m + n) is 3, so this is a third-order reaction, a reaction whose rate is determined by three reactants. The units of the rate constant become more complex as the overall reaction order increases.
Exercise
The peroxydisulfate ion (S2O82−) is a potent oxidizing agent that reacts rapidly with iodide ion in water:
S2O82−(aq) + 3I−(aq) → 2SO42−(aq) + I3−(aq)The following table lists kinetics data for this reaction at 25°C. Determine the rate law and calculate the rate constant.
| Experiment | [S2O82−]0 (M) | [I−]0 (M) | Initial Rate (M/s) |
|---|---|---|---|
| 1 | 0.27 | 0.38 | 2.05 |
| 2 | 0.40 | 0.38 | 3.06 |
| 3 | 0.40 | 0.22 | 1.76 |
Answer: rate = k[S2O82−][I−]; k = 20 M−1·s−1
Summary
The reaction rate of a zeroth-order reaction is independent of the concentration of the reactants. The reaction rate of a first-order reaction is directly proportional to the concentration of one reactant. The reaction rate of a simple second-order reaction is proportional to the square of the concentration of one reactant. Knowing the rate law of a reaction gives clues to the reaction mechanism.
Key Takeaway
- Either the differential rate law or the integrated rate law can be used to determine the reaction order from experimental data.
Key Equations
zeroth-order reaction
Equation 14.16: [A] = [A]0 − kt
first-order reaction
Equation 14.20: [A] = [A]0e−kt
Equation 14.21: ln[A] = ln[A]0 − kt
second-order reaction
Conceptual Problems
-
What are the characteristics of a zeroth-order reaction? Experimentally, how would you determine whether a reaction is zeroth order?
-
Predict whether the following reactions are zeroth order and explain your reasoning.
- a substitution reaction of an alcohol with HCl to form an alkyl halide and water
- catalytic hydrogenation of an alkene
- hydrolysis of an alkyl halide to an alcohol
- enzymatic conversion of nitrate to nitrite in a soil bacterium
-
In a first-order reaction, what is the advantage of using the integrated rate law expressed in natural logarithms over the rate law expressed in exponential form?
-
If the reaction rate is directly proportional to the concentration of a reactant, what does this tell you about (a) the reaction order with respect to the reactant and (b) the overall reaction order?
-
The reaction of NO with O2 is found to be second order with respect to NO and first order with respect to O2. What is the overall reaction order? What is the effect of doubling the concentration of each reagent on the reaction rate?
Numerical Problems
-
Iodide reduces Fe(III) according to the following reaction:
2Fe3+(soln) + 2I−(soln) → 2Fe2+(soln) + I2(soln)Experimentally, it was found that doubling the concentration of Fe(III) doubled the reaction rate, and doubling the iodide concentration increased the reaction rate by a factor of 4. What is the reaction order with respect to each species? What is the overall rate law? What is the overall reaction order?
-
Benzoyl peroxide is a medication used to treat acne. Its rate of thermal decomposition at several concentrations was determined experimentally, and the data were tabulated as follows:
Experiment [Benzoyl Peroxide]0 (M) Initial Rate (M/s) 1 1.00 2.22 × 10−4 2 0.70 1.64 × 10−4 3 0.50 1.12 × 10−4 4 0.25 0.59 × 10−4 What is the reaction order with respect to benzoyl peroxide? What is the rate law for this reaction?
-
1-Bromopropane is a colorless liquid that reacts with S2O32− according to the following reaction:
C3H7Br + S2O32− → C3H7S2O3− + Br−The reaction is first order in 1-bromopropane and first order in S2O32−, with a rate constant of 8.05 × 10−4 M−1·s−1. If you began a reaction with 40 mmol/100 mL of C3H7Br and an equivalent concentration of S2O32−, what would the initial reaction rate be? If you were to decrease the concentration of each reactant to 20 mmol/100 mL, what would the initial reaction rate be?
-
The experimental rate law for the reaction 3A + 2B → C + D was found to be Δ[C]/Δt = k[A]2[B] for an overall reaction that is third order. Because graphical analysis is difficult beyond second-order reactions, explain the procedure for determining the rate law experimentally.
Answers
-
First order in Fe3+; second order in I−; third order overall; rate = k[Fe3+][I−]2.
-
-
1.29 × 10−4 M/s; 3.22 × 10−5 M/s
-
14.4 Using Graphs to Determine Rate Laws, Rate Constants, and Reaction Orders
Learning Objective
- To use graphs to analyze the kinetics of a reaction.
In Section 14.3 "Methods of Determining Reaction Order", you learned that the integrated rate law for each common type of reaction (zeroth, first, or second order in a single reactant) can be plotted as a straight line. Using these plots offers an alternative to the methods described for showing how reactant concentration changes with time and determining reaction order.
We will illustrate the use of these graphs by considering the thermal decomposition of NO2 gas at elevated temperatures, which occurs according to the following reaction:
Equation 14.26
Experimental data for this reaction at 330°C are listed in Table 14.5 "Concentration of NO"; they are provided as [NO2], ln[NO2], and 1/[NO2] versus time to correspond to the integrated rate laws for zeroth-, first-, and second-order reactions, respectively. The actual concentrations of NO2 are plotted versus time in part (a) in Figure 14.15 "The Decomposition of NO". Because the plot of [NO2] versus t is not a straight line, we know the reaction is not zeroth order in NO2. A plot of ln[NO2] versus t (part (b) in Figure 14.15 "The Decomposition of NO") shows us that the reaction is not first order in NO2 because a first-order reaction would give a straight line. Having eliminated zeroth-order and first-order behavior, we construct a plot of 1/[NO2] versus t (part (c) in Figure 14.15 "The Decomposition of NO"). This plot is a straight line, indicating that the reaction is second order in NO2.
Table 14.5 Concentration of NO2 as a Function of Time at 330°C
| Time (s) | [NO2] (M) | ln[NO2] | 1/[NO2] (M−1) |
|---|---|---|---|
| 0 | 1.00 × 10−2 | −4.605 | 100 |
| 60 | 6.83 × 10−3 | −4.986 | 146 |
| 120 | 5.18 × 10−3 | −5.263 | 193 |
| 180 | 4.18 × 10−3 | −5.477 | 239 |
| 240 | 3.50 × 10−3 | −5.655 | 286 |
| 300 | 3.01 × 10−3 | −5.806 | 332 |
| 360 | 2.64 × 10−3 | −5.937 | 379 |
Figure 14.15 The Decomposition of NO2
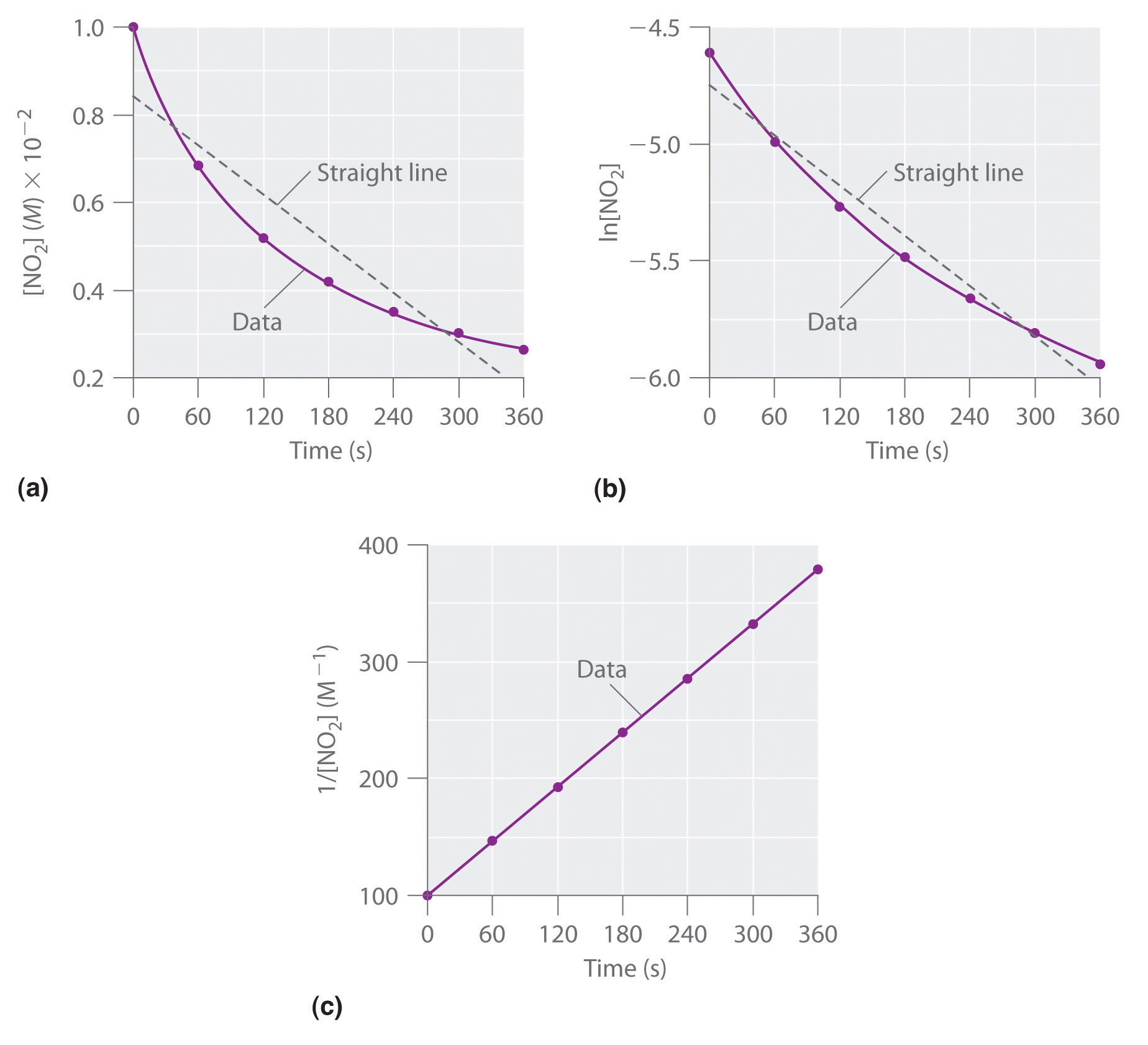
These plots show the decomposition of a sample of NO2 at 330°C as (a) the concentration of NO2 versus t, (b) the natural logarithm of [NO2] versus t, and (c) 1/[NO2] versus t.
We have just determined the reaction order using data from a single experiment by plotting the concentration of the reactant as a function of time. Because of the characteristic shapes of the lines shown in Figure 14.16 "Properties of Reactions That Obey Zeroth-, First-, and Second-Order Rate Laws", the graphs can be used to determine the reaction order of an unknown reaction. In contrast, the method described in Section 14.3 "Methods of Determining Reaction Order" required multiple experiments at different NO2 concentrations as well as accurate initial rates of reaction, which can be difficult to obtain for rapid reactions.
Figure 14.16 Properties of Reactions That Obey Zeroth-, First-, and Second-Order Rate Laws
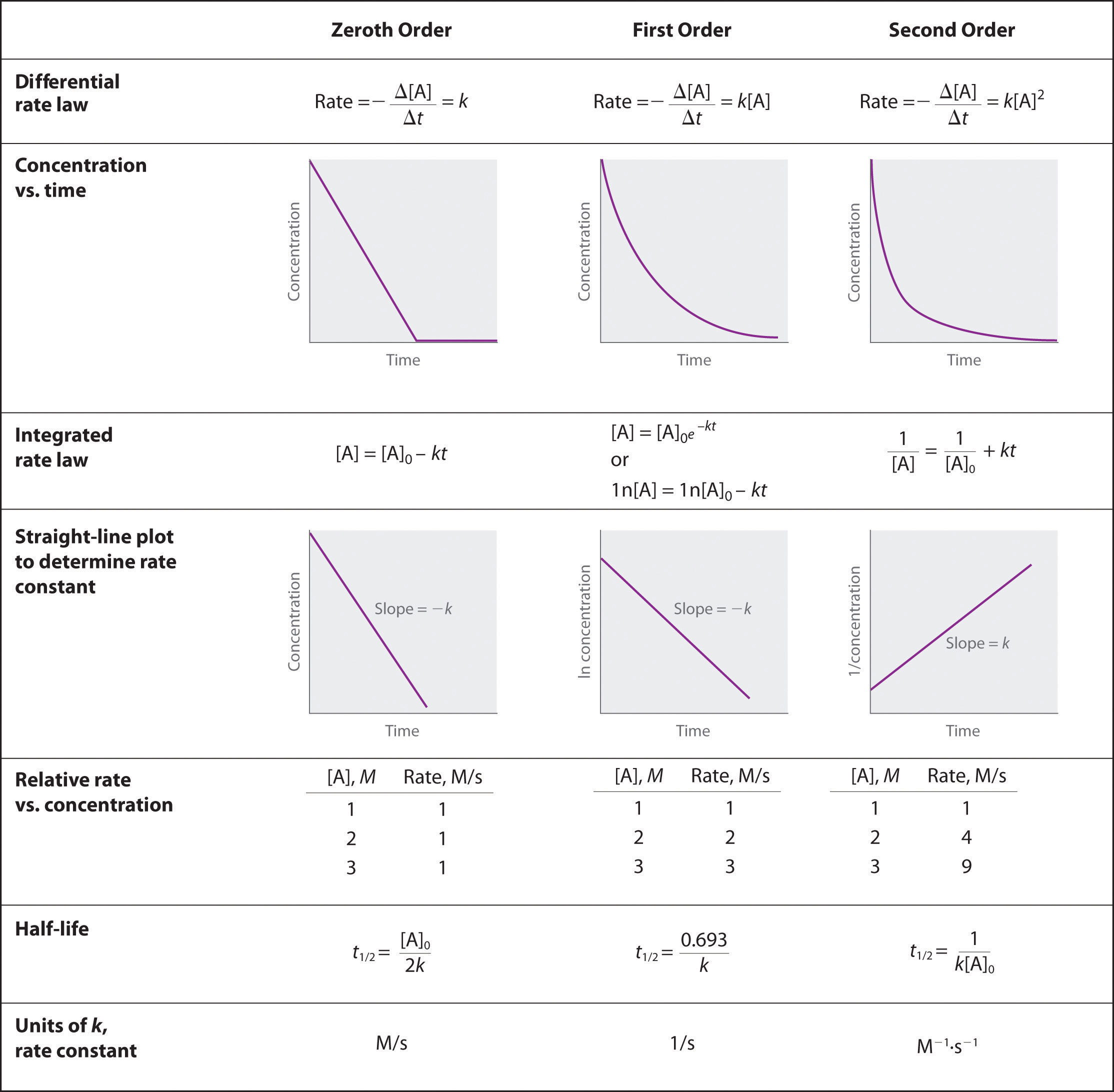
Example 9
Dinitrogen pentoxide (N2O5) decomposes to NO2 and O2 at relatively low temperatures in the following reaction:
2N2O5(soln) → 4NO2(soln) + O2(g)This reaction is carried out in a CCl4 solution at 45°C. The concentrations of N2O5 as a function of time are listed in the following table, together with the natural logarithms and reciprocal N2O5 concentrations. Plot a graph of the concentration versus t, ln concentration versus t, and 1/concentration versus t and then determine the rate law and calculate the rate constant.
| Time (s) | [N2O5] (M) | ln[N2O5] | 1/[N2O5] (M−1) |
|---|---|---|---|
| 0 | 0.0365 | −3.310 | 27.4 |
| 600 | 0.0274 | −3.597 | 36.5 |
| 1200 | 0.0206 | −3.882 | 48.5 |
| 1800 | 0.0157 | −4.154 | 63.7 |
| 2400 | 0.0117 | −4.448 | 85.5 |
| 3000 | 0.00860 | −4.756 | 116 |
| 3600 | 0.00640 | −5.051 | 156 |
Given: balanced chemical equation, reaction times, and concentrations
Asked for: graph of data, rate law, and rate constant
Strategy:
A Use the data in the table to separately plot concentration, the natural logarithm of the concentration, and the reciprocal of the concentration (the vertical axis) versus time (the horizontal axis). Compare the graphs with those in Figure 14.16 "Properties of Reactions That Obey Zeroth-, First-, and Second-Order Rate Laws" to determine the reaction order.
B Write the rate law for the reaction. Using the appropriate data from the table and the linear graph corresponding to the rate law for the reaction, calculate the slope of the plotted line to obtain the rate constant for the reaction.
Solution:
A Here are plots of [N2O5] versus t, ln[N2O5] versus t, and 1/[N2O5] versus t:
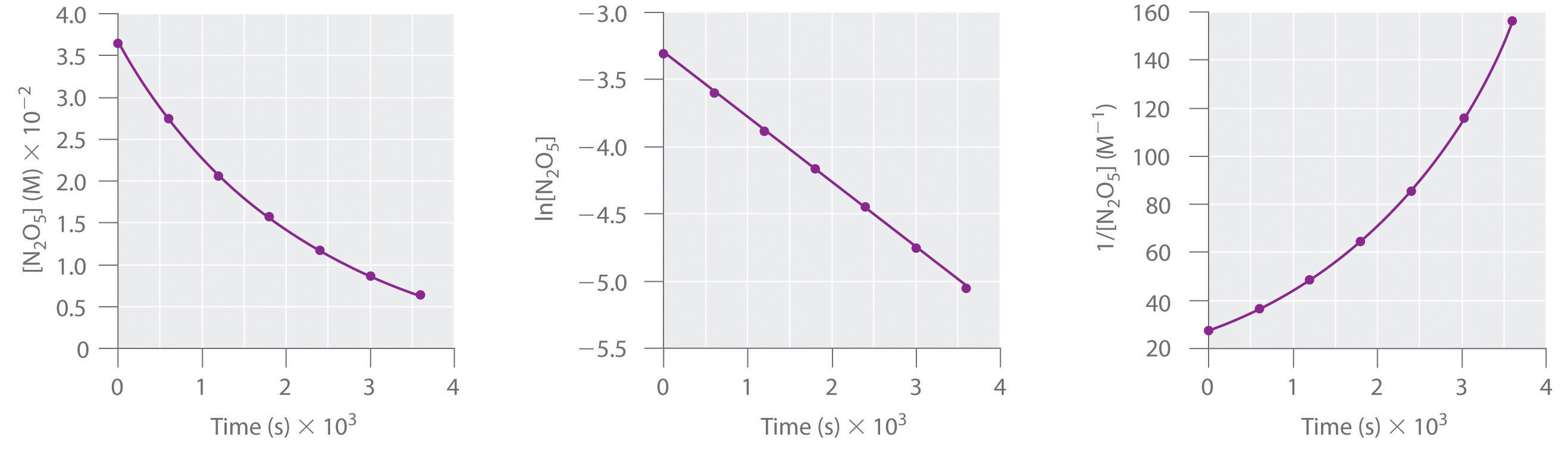
The plot of ln[N2O5] versus t gives a straight line, whereas the plots of [N2O5] versus t and 1/[N2O5] versus t do not. This means that the decomposition of N2O5 is first order in [N2O5].
B The rate law for the reaction is therefore
rate = k[N2O5]Calculating the rate constant is straightforward because we know that the slope of the plot of ln[A] versus t for a first-order reaction is −k. We can calculate the slope using any two points that lie on the line in the plot of ln[N2O5] versus t. Using the points for t = 0 and 3000 s,
Thus k = 4.820 × 10−4 s−1.
Exercise
1,3-Butadiene (CH2=CH—CH=CH2; C4H6) is a volatile and reactive organic molecule used in the production of rubber. Above room temperature, it reacts slowly to form products. Concentrations of C4H6 as a function of time at 326°C are listed in the following table along with ln[C4H6] and the reciprocal concentrations. Graph the data as concentration versus t, ln concentration versus t, and 1/concentration versus t. Then determine the reaction order in C4H6, the rate law, and the rate constant for the reaction.
| Time (s) | [C4H6] (M) | ln[C4H6] | 1/[C4H6] (M−1) |
|---|---|---|---|
| 0 | 1.72 × 10−2 | −4.063 | 58.1 |
| 900 | 1.43 × 10−2 | −4.247 | 69.9 |
| 1800 | 1.23 × 10−2 | −4.398 | 81.3 |
| 3600 | 9.52 × 10−3 | −4.654 | 105 |
| 6000 | 7.30 × 10−3 | −4.920 | 137 |
Answer:
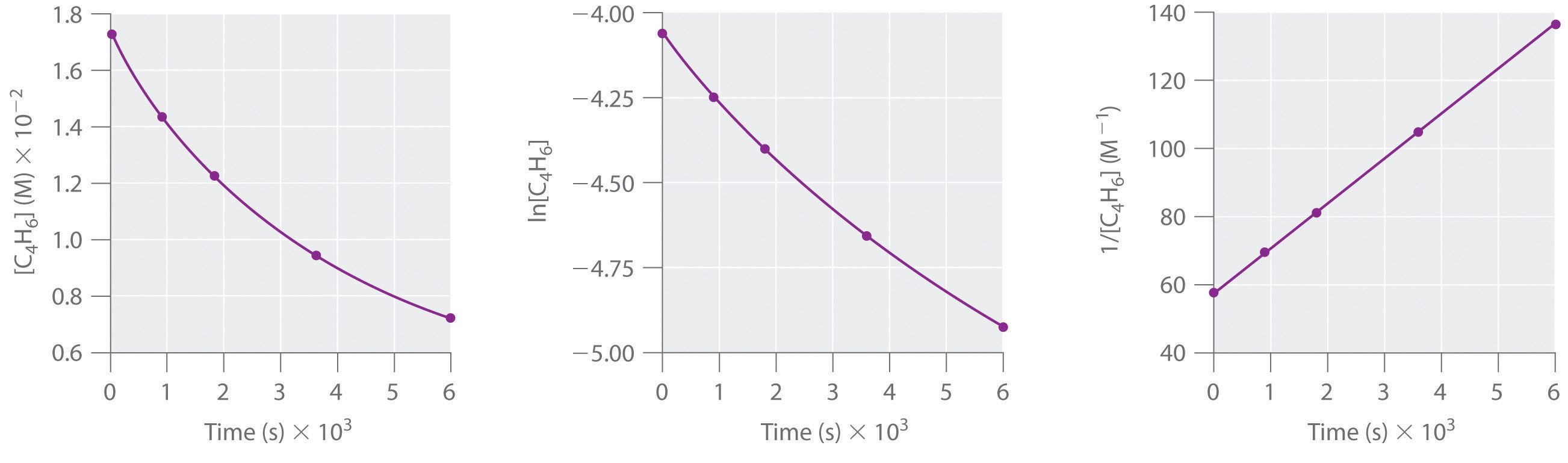
second order in C4H6; rate = k[C4H6]2; k = 1.3 × 10−2 M−1·s−1
Summary
For a zeroth-order reaction, a plot of the concentration of any reactant versus time is a straight line with a slope of −k. For a first-order reaction, a plot of the natural logarithm of the concentration of a reactant versus time is a straight line with a slope of −k. For a second-order reaction, a plot of the inverse of the concentration of a reactant versus time is a straight line with a slope of k.
Key Takeaway
- Plotting the concentration of a reactant as a function of time produces a graph with a characteristic shape that can be used to identify the reaction order in that reactant.
Conceptual Problems
-
Compare first-order differential and integrated rate laws with respect to the following. Is there any information that can be obtained from the integrated rate law that cannot be obtained from the differential rate law?
- the magnitude of the rate constant
- the information needed to determine the order
- the shape of the graphs
-
In the single-step, second-order reaction 2A → products, how would a graph of [A] versus time compare to a plot of 1/[A] versus time? Which of these would be the most similar to the same set of graphs for A during the single-step, second-order reaction A + B → products? Explain.
-
For reactions of the same order, what is the relationship between the magnitude of the rate constant and the reaction rate? If you were comparing reactions with different orders, could the same arguments be made? Why?
Answers
-
- For a given reaction under particular conditions, the magnitude of the first-order rate constant does not depend on whether a differential rate law or an integrated rate law is used.
- The differential rate law requires multiple experiments to determine reactant order; the integrated rate law needs only one experiment.
- Using the differential rate law, a graph of concentration versus time is a curve with a slope that becomes less negative with time, whereas for the integrated rate law, a graph of ln[reactant] versus time gives a straight line with slope = −k. The integrated rate law allows you to calculate the concentration of a reactant at any time during the reaction; the differential rate law does not.
-
-
The reaction rate increases as the rate constant increases. We cannot directly compare reaction rates and rate constants for reactions of different orders because they are not mathematically equivalent.
Numerical Problems
-
One method of using graphs to determine reaction order is to use relative rate information. Plotting the log of the relative rate versus log of relative concentration provides information about the reaction. Here is an example of data from a zeroth-order reaction:
Relative [A] (M) Relative Rate (M/s) 1 1 2 1 3 1 Varying [A] does not alter the reaction rate. Using the relative rates in the table, generate plots of log(rate) versus log(concentration) for zeroth-, first- and second-order reactions. What does the slope of each line represent?
-
The table below follows the decomposition of N2O5 gas by examining the partial pressure of the gas as a function of time at 45°C. What is the reaction order? What is the rate constant? How long would it take for the pressure to reach 105 mmHg at 45°C?
Time (s) Pressure (mmHg) 0 348 400 276 1600 156 3200 69 4800 33
14.5 Half-Lives and Radioactive Decay Kinetics
Learning Objective
- To know how to use half-lives to describe the rates of first-order reactions.
Half-Lives
Another approach to describing reaction rates is based on the time required for the concentration of a reactant to decrease to one-half its initial value. This period of time is called the half-lifeThe period of time it takes for the concentration of a reactant to decrease to one-half its initial value. of the reaction, written as t1/2. Thus the half-life of a reaction is the time required for the reactant concentration to decrease from [A]0 to [A]0/2. If two reactions have the same order, the faster reaction will have a shorter half-life, and the slower reaction will have a longer half-life.
The half-life of a first-order reaction under a given set of reaction conditions is a constant. This is not true for zeroth- and second-order reactions. The half-life of a first-order reaction is independent of the concentration of the reactants. This becomes evident when we rearrange the integrated rate law for a first-order reaction (Equation 14.21) to produce the following equation:
Equation 14.27
Substituting [A]0/2 for [A] and t1/2 for t (to indicate a half-life) into Equation 14.27 gives
The natural logarithm of 2 (to three decimal places) is 0.693. Substituting this value into the equation, we obtain the expression for the half-life of a first-order reaction:
Equation 14.28
Thus, for a first-order reaction, each successive half-life is the same length of time, as shown in Figure 14.17 "The Half-Life of a First-Order Reaction", and is independent of [A].
Figure 14.17 The Half-Life of a First-Order Reaction
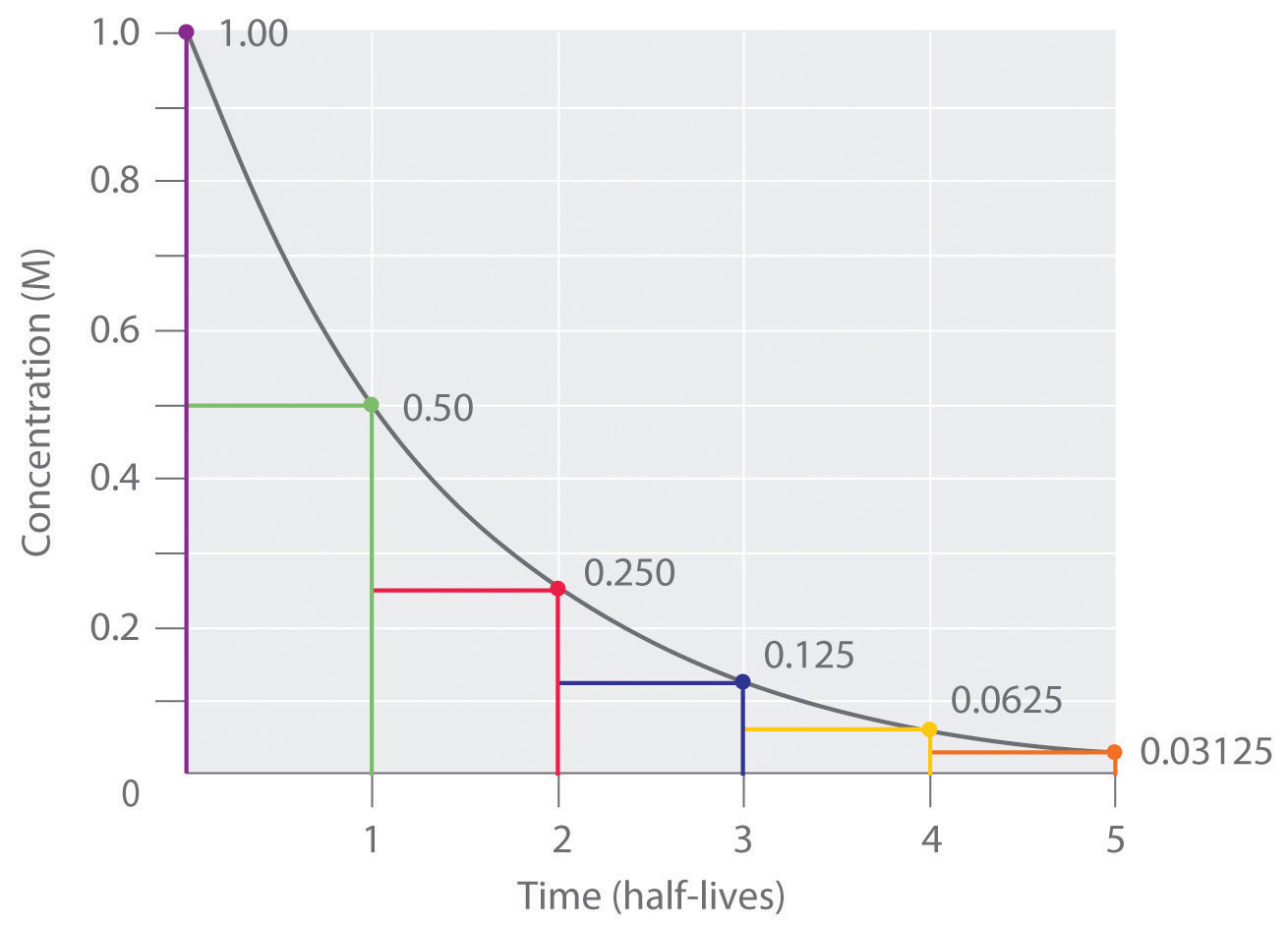
This plot shows the concentration of the reactant in a first-order reaction as a function of time and identifies a series of half-lives, intervals in which the reactant concentration decreases by a factor of 2. In a first-order reaction, every half-life is the same length of time.
If we know the rate constant for a first-order reaction, then we can use half-lives to predict how much time is needed for the reaction to reach a certain percent completion.
| Number of Half-Lives | Percentage of Reactant Remaining | |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| n | ||
As you can see from this table, the amount of reactant left after n half-lives of a first-order reaction is (1/2)n times the initial concentration.
Note the Pattern
For a first-order reaction, the concentration of the reactant decreases by a constant with each half-life and is independent of [A].
Example 10
The anticancer drug cisplatin hydrolyzes in water with a rate constant of 1.5 × 10−3 min−1 at pH 7.0 and 25°C. Calculate the half-life for the hydrolysis reaction under these conditions. If a freshly prepared solution of cisplatin has a concentration of 0.053 M, what will be the concentration of cisplatin after 5 half-lives? after 10 half-lives? What is the percent completion of the reaction after 5 half-lives? after 10 half-lives?
Given: rate constant, initial concentration, and number of half-lives
Asked for: half-life, final concentrations, and percent completion
Strategy:
A Use Equation 14.28 to calculate the half-life of the reaction.
B Multiply the initial concentration by 1/2 to the power corresponding to the number of half-lives to obtain the remaining concentrations after those half-lives.
C Subtract the remaining concentration from the initial concentration. Then divide by the initial concentration, multiplying the fraction by 100 to obtain the percent completion.
Solution:
A We can calculate the half-life of the reaction using Equation 14.28:
Thus it takes almost 8 h for half of the cisplatin to hydrolyze.
B After 5 half-lives (about 38 h), the remaining concentration of cisplatin will be as follows:
After 10 half-lives (77 h), the remaining concentration of cisplatin will be as follows:
C The percent completion after 5 half-lives will be as follows:
The percent completion after 10 half-lives will be as follows:
Thus a first-order chemical reaction is 97% complete after 5 half-lives and 100% complete after 10 half-lives.
Exercise
In Example 4 you found that ethyl chloride decomposes to ethylene and HCl in a first-order reaction that has a rate constant of 1.6 × 10−6 s−1 at 650°C. What is the half-life for the reaction under these conditions? If a flask that originally contains 0.077 M ethyl chloride is heated at 650°C, what is the concentration of ethyl chloride after 4 half-lives?
Answer: 4.3 × 105 s = 120 h = 5.0 days; 4.8 × 10−3 M
Radioactive Decay Rates
As you learned in Chapter 1 "Introduction to Chemistry", radioactivity, or radioactive decay, is the emission of a particle or a photon that results from the spontaneous decomposition of the unstable nucleus of an atom. The rate of radioactive decay is an intrinsic property of each radioactive isotope that is independent of the chemical and physical form of the radioactive isotope. The rate is also independent of temperature. In this section, we will describe radioactive decay rates and how half-lives can be used to monitor radioactive decay processes.
In any sample of a given radioactive substance, the number of atoms of the radioactive isotope must decrease with time as their nuclei decay to nuclei of a more stable isotope. Using N to represent the number of atoms of the radioactive isotope, we can define the rate of decayThe decrease in the number of a radioisotope’s nuclei per unit time. of the sample, which is also called its activity (A)The decrease in the number of a radioisotope’s nuclei per unit time: as the decrease in the number of the radioisotope’s nuclei per unit time:
Equation 14.29
Activity is usually measured in disintegrations per second (dps) or disintegrations per minute (dpm).
The activity of a sample is directly proportional to the number of atoms of the radioactive isotope in the sample:
Equation 14.30
A = kNHere, the symbol k is the radioactive decay constant, which has units of inverse time (e.g., s−1, yr−1) and a characteristic value for each radioactive isotope. If we combine Equation 14.29 and Equation 14.30, we obtain the relationship between the number of decays per unit time and the number of atoms of the isotope in a sample:
Equation 14.31
Equation 14.31 is the same as the equation for the reaction rate of a first-order reaction (Equation 14.19), except that it uses numbers of atoms instead of concentrations. In fact, radioactive decay is a first-order process and can be described in terms of either the differential rate law (Equation 14.31) or the integrated rate law:
N = N0e−ktEquation 14.32
Because radioactive decay is a first-order process, the time required for half of the nuclei in any sample of a radioactive isotope to decay is a constant, called the half-life of the isotope. The half-life tells us how radioactive an isotope is (the number of decays per unit time); thus it is the most commonly cited property of any radioisotope. For a given number of atoms, isotopes with shorter half-lives decay more rapidly, undergoing a greater number of radioactive decays per unit time than do isotopes with longer half-lives. The half-lives of several isotopes are listed in Table 14.6 "Half-Lives and Applications of Some Radioactive Isotopes", along with some of their applications.
Table 14.6 Half-Lives and Applications of Some Radioactive Isotopes
| Radioactive Isotope | Half-Life | Typical Uses |
|---|---|---|
| hydrogen-3 (tritium) | 12.32 yr | biochemical tracer |
| carbon-11 | 20.33 min | positron emission tomography (biomedical imaging) |
| carbon-14 | 5.70 × 103 yr | dating of artifacts |
| sodium-24 | 14.951 h | cardiovascular system tracer |
| phosphorus-32 | 14.26 days | biochemical tracer |
| potassium-40 | 1.248 × 109 yr | dating of rocks |
| iron-59 | 44.495 days | red blood cell lifetime tracer |
| cobalt-60 | 5.2712 yr | radiation therapy for cancer |
| technetium-99m* | 6.006 h | biomedical imaging |
| iodine-131 | 8.0207 days | thyroid studies tracer |
| radium-226 | 1.600 × 103 yr | radiation therapy for cancer |
| uranium-238 | 4.468 × 109 yr | dating of rocks and Earth’s crust |
| americium-241 | 432.2 yr | smoke detectors |
| *The m denotes metastable, where an excited state nucleus decays to the ground state of the same isotope. | ||
Note the Pattern
Radioactive decay is a first-order process.
Radioisotope Dating Techniques
In our earlier discussion, we used the half-life of a first-order reaction to calculate how long the reaction had been occurring. Because nuclear decay reactions follow first-order kinetics and have a rate constant that is independent of temperature and the chemical or physical environment, we can perform similar calculations using the half-lives of isotopes to estimate the ages of geological and archaeological artifacts. The techniques that have been developed for this application are known as radioisotope dating techniques.
The most common method for measuring the age of ancient objects is carbon-14 dating. The carbon-14 isotope, created continuously in the upper regions of Earth’s atmosphere, reacts with atmospheric oxygen or ozone to form 14CO2. As a result, the CO2 that plants use as a carbon source for synthesizing organic compounds always includes a certain proportion of 14CO2 molecules as well as nonradioactive 12CO2 and 13CO2. Any animal that eats a plant ingests a mixture of organic compounds that contains approximately the same proportions of carbon isotopes as those in the atmosphere. When the animal or plant dies, the carbon-14 nuclei in its tissues decay to nitrogen-14 nuclei by a radioactive process known as beta decay, which releases low-energy electrons (β particles) that can be detected and measured:
Equation 14.33
14C → 14N + β−The half-life for this reaction is 5700 ± 30 yr.
The 14C/12C ratio in living organisms is 1.3 × 10−12, with a decay rate of 15 dpm/g of carbon (Figure 14.18 "Radiocarbon Dating"). Comparing the disintegrations per minute per gram of carbon from an archaeological sample with those from a recently living sample enables scientists to estimate the age of the artifact, as illustrated in Example 11.Using this method implicitly assumes that the 14CO2/12CO2 ratio in the atmosphere is constant, which is not strictly correct. Other methods, such as tree-ring dating, have been used to calibrate the dates obtained by radiocarbon dating, and all radiocarbon dates reported are now corrected for minor changes in the 14CO2/12CO2 ratio over time.
Figure 14.18 Radiocarbon Dating
A plot of the specific activity of 14C versus age for a number of archaeological samples shows an inverse linear relationship between 14C content (a log scale) and age (a linear scale).
Example 11
In 1990, the remains of an apparently prehistoric man were found in a melting glacier in the Italian Alps. Analysis of the 14C content of samples of wood from his tools gave a decay rate of 8.0 dpm/g carbon. How long ago did the man die?
Given: isotope and final activity
Asked for: elapsed time
Strategy:
A Use Equation 14.30 to calculate N0/N. Then substitute the value for the half-life of 14C into Equation 14.28 to find the rate constant for the reaction.
B Using the values obtained for N0/N and the rate constant, solve Equation 14.32 to obtain the elapsed time.
Solution:
We know the initial activity from the isotope’s identity (15 dpm/g), the final activity (8.0 dpm/g), and the half-life, so we can use the integrated rate law for a first-order nuclear reaction (Equation 14.32) to calculate the elapsed time (the amount of time elapsed since the wood for the tools was cut and began to decay).
A From Equation 14.30, we know that A = kN. We can therefore use the initial and final activities (A0 = 15 dpm and A = 8.0 dpm) to calculate N0/N:
Now we need only calculate the rate constant for the reaction from its half-life (5730 yr) using Equation 14.28:
This equation can be rearranged as follows:
B Substituting into the equation for t,
From our calculations, the man died 5200 yr ago.
Exercise
It is believed that humans first arrived in the Western Hemisphere during the last Ice Age, presumably by traveling over an exposed land bridge between Siberia and Alaska. Archaeologists have estimated that this occurred about 11,000 yr ago, but some argue that recent discoveries in several sites in North and South America suggest a much earlier arrival. Analysis of a sample of charcoal from a fire in one such site gave a 14C decay rate of 0.4 dpm/g of carbon. What is the approximate age of the sample?
Answer: 30,000 yr
Summary
The half-life of a reaction is the time required for the reactant concentration to decrease to one-half its initial value. The half-life of a first-order reaction is a constant that is related to the rate constant for the reaction: t1/2 = 0.693/k.
Radioactive decay reactions are first-order reactions. The rate of decay, or activity, of a sample of a radioactive substance is the decrease in the number of radioactive nuclei per unit time.
Key Takeaways
- The half-life of a first-order reaction is independent of the concentration of the reactants.
- The half-lives of radioactive isotopes can be used to date objects.
Conceptual Problems
-
What do chemists mean by the half-life of a reaction?
-
If a sample of one isotope undergoes more disintegrations per second than the same number of atoms of another isotope, how do their half-lives compare?
Numerical Problems
-
Half-lives for the reaction A + B → C were calculated at three values of [A]0, and [B] was the same in all cases. The data are listed in the following table:
[A]0 (M) t½ (s) 0.50 420 0.75 280 1.0 210 Does this reaction follow first-order kinetics? On what do you base your answer?
-
Ethyl-2-nitrobenzoate (NO2C6H4CO2C2H5) hydrolyzes under basic conditions. A plot of [NO2C6H4CO2C2H5] versus t was used to calculate t½, with the following results:
[NO2C6H4CO2C2H5] (M/cm3) t½ (s) 0.050 240 0.040 300 0.030 400 Is this a first-order reaction? Explain your reasoning.
-
Azomethane (CH3N2CH3) decomposes at 600 K to C2H6 and N2. The decomposition is first order in azomethane. Calculate t½ from the data in the following table:
Time (s) (atm) 0 8.2 × 10−2 2000 3.99 × 10−2 4000 1.94 × 10−2 How long will it take for the decomposition to be 99.9% complete?
-
The first-order decomposition of hydrogen peroxide has a half-life of 10.7 h at 20°C. What is the rate constant (expressed in s−1) for this reaction? If you started with a solution that was 7.5 × 10−3 M H2O2, what would be the initial rate of decomposition (M/s)? What would be the concentration of H2O2 after 3.3 h?
Answers
-
No; the reaction is second order in A because the half-life decreases with increasing reactant concentration according to t1/2 = 1/k[A0].
-
-
t1/2 = 1.92 × 103 s or 1920 s; 19100 s or 5.32 hrs.
-
14.6 Reaction Rates—A Microscopic View
Learning Objective
- To determine the individual steps of a simple reaction.
One of the major reasons for studying chemical kinetics is to use measurements of the macroscopic properties of a system, such as the rate of change in the concentration of reactants or products with time, to discover the sequence of events that occur at the molecular level during a reaction. This molecular description is the mechanism of the reaction; it describes how individual atoms, ions, or molecules interact to form particular products. The stepwise changes are collectively called the reaction mechanism.
In an internal combustion engine, for example, isooctane reacts with oxygen to give carbon dioxide and water:
Equation 14.34
2C8H18(l) + 25O2(g) → 16CO2(g) + 18H2O(g)For this reaction to occur in a single step, 25 dioxygen molecules and 2 isooctane molecules would have to collide simultaneously and be converted to 34 molecules of product, which is very unlikely. It is more likely that a complex series of reactions takes place in a stepwise fashion. Each individual reaction, which is called an elementary reactionEach of the complex series of reactions that take place in a stepwise fashion to convert reactants to products., involves one, two, or (rarely) three atoms, molecules, or ions. The overall sequence of elementary reactions is the mechanism of the reaction. The sum of the individual steps, or elementary reactions, in the mechanism must give the balanced chemical equation for the overall reaction.
Molecularity and the Rate-Determining Step
To demonstrate how the analysis of elementary reactions helps us determine the overall reaction mechanism, we will examine the much simpler reaction of carbon monoxide with nitrogen dioxide.
Equation 14.35
NO2(g) + CO(g) → NO(g) + CO2(g)From the balanced chemical equation, one might expect the reaction to occur via a collision of one molecule of NO2 with a molecule of CO that results in the transfer of an oxygen atom from nitrogen to carbon. The experimentally determined rate law for the reaction, however, is as follows:
Equation 14.36
rate = k[NO2]2The fact that the reaction is second order in [NO2] and independent of [CO] tells us that it does not occur by the simple collision model outlined previously. If it did, its predicted rate law would be rate = k[NO2][CO].
The following two-step mechanism is consistent with the rate law if step 1 is much slower than step 2:
According to this mechanism, the overall reaction occurs in two steps, or elementary reactions. Summing steps 1 and 2 and canceling on both sides of the equation gives the overall balanced chemical equation for the reaction. The NO3 molecule is an intermediateA species in a reaction mechanism that does not appear in the balanced chemical equation for the overall reaction. in the reaction, a species that does not appear in the balanced chemical equation for the overall reaction. It is formed as a product of the first step but is consumed in the second step.
Note the Pattern
The sum of the elementary reactions in a reaction mechanism must give the overall balanced chemical equation of the reaction.
Using Molecularity to Describe a Rate Law
The molecularityThe number of molecules that collide during any step in a reaction mechanism. of an elementary reaction is the number of molecules that collide during that step in the mechanism. If there is only a single reactant molecule in an elementary reaction, that step is designated as unimolecular; if there are two reactant molecules, it is bimolecular; and if there are three reactant molecules (a relatively rare situation), it is termolecular. Elementary reactions that involve the simultaneous collision of more than three molecules are highly improbable and have never been observed experimentally. (To understand why, try to make three or more marbles or pool balls collide with one another simultaneously!)
Writing the rate law for an elementary reaction is straightforward because we know how many molecules must collide simultaneously for the elementary reaction to occur; hence the order of the elementary reaction is the same as its molecularity (Table 14.7 "Common Types of Elementary Reactions and Their Rate Laws"). In contrast, the rate law for the reaction cannot be determined from the balanced chemical equation for the overall reaction. The general rate law for a unimolecular elementary reaction (A → products) is rate = k[A]. For bimolecular reactions, the reaction rate depends on the number of collisions per unit time, which is proportional to the product of the concentrations of the reactants, as shown in Figure 14.19 "The Basis for Writing Rate Laws of Elementary Reactions". For a bimolecular elementary reaction of the form A + B → products, the general rate law is rate = k[A][B].
Table 14.7 Common Types of Elementary Reactions and Their Rate Laws
| Elementary Reaction | Molecularity | Rate Law | Reaction Order |
|---|---|---|---|
| A → products | unimolecular | rate = k[A] | first |
| 2A → products | bimolecular | rate = k[A]2 | second |
| A + B → products | bimolecular | rate = k[A][B] | second |
| 2A + B → products | termolecular | rate = k[A]2[B] | third |
| A + B + C → products | termolecular | rate = k[A][B][C] | third |
Figure 14.19 The Basis for Writing Rate Laws of Elementary Reactions

This diagram illustrates how the number of possible collisions per unit time between two reactant species, A and B, depends on the number of A and B particles present. The number of collisions between A and B particles increases as the product of the number of particles, not as the sum. This is why the rate law for an elementary reaction depends on the product of the concentrations of the species that collide in that step.
Identifying the Rate-Determining Step
Note the important difference between writing rate laws for elementary reactions and the balanced chemical equation of the overall reaction. Because the balanced chemical equation does not necessarily reveal the individual elementary reactions by which the reaction occurs, we cannot obtain the rate law for a reaction from the overall balanced chemical equation alone. In fact, it is the rate law for the slowest overall reaction, which is the same as the rate law for the slowest step in the reaction mechanism, the rate-determining stepThe slowest step in a reaction mechanism., that must give the experimentally determined rate law for the overall reaction.This statement is true if one step is substantially slower than all the others, typically by a factor of 10 or more. If two or more slow steps have comparable rates, the experimentally determined rate laws can become complex. Our discussion is limited to reactions in which one step can be identified as being substantially slower than any other. The reason for this is that any process that occurs through a sequence of steps can take place no faster than the slowest step in the sequence. In an automotive assembly line, for example, a component cannot be used faster than it is produced. Similarly, blood pressure is regulated by the flow of blood through the smallest passages, the capillaries. Because movement through capillaries constitutes the rate-determining step in blood flow, blood pressure can be regulated by medications that cause the capillaries to contract or dilate. A chemical reaction that occurs via a series of elementary reactions can take place no faster than the slowest step in the series of reactions.

Rate-determining step. The phenomenon of a rate-determining step can be compared to a succession of funnels. The smallest-diameter funnel controls the rate at which the bottle is filled, whether it is the first or the last in the series. Pouring liquid into the first funnel faster than it can drain through the smallest results in an overflow.
Look at the rate laws for each elementary reaction in our example as well as for the overall reaction.
The experimentally determined rate law for the reaction of NO2 with CO is the same as the predicted rate law for step 1. This tells us that the first elementary reaction is the rate-determining step, so k for the overall reaction must equal k1. That is, NO3 is formed slowly in step 1, but once it is formed, it reacts very rapidly with CO in step 2.
Sometimes chemists are able to propose two or more mechanisms that are consistent with the available data. If a proposed mechanism predicts the wrong experimental rate law, however, the mechanism must be incorrect.
Example 12
In an alternative mechanism for the reaction of NO2 with CO, N2O4 appears as an intermediate.
Write the rate law for each elementary reaction. Is this mechanism consistent with the experimentally determined rate law (rate = k[NO2]2)?
Given: elementary reactions
Asked for: rate law for each elementary reaction and overall rate law
Strategy:
A Determine the rate law for each elementary reaction in the reaction.
B Determine which rate law corresponds to the experimentally determined rate law for the reaction. This rate law is the one for the rate-determining step.
Solution:
A The rate law for step 1 is rate = k1[NO2]2; for step 2, it is rate = k2[N2O4][CO].
B If step 1 is slow (and therefore the rate-determining step), then the overall rate law for the reaction will be the same: rate = k1[NO2]2. This is the same as the experimentally determined rate law. Hence this mechanism, with N2O4 as an intermediate, and the one described previously, with NO3 as an intermediate, are kinetically indistinguishable. In this case, further experiments are needed to distinguish between them. For example, the researcher could try to detect the proposed intermediates, NO3 and N2O4, directly.
Exercise A
Iodine monochloride (ICl) reacts with H2 as follows:
2ICl(l) + H2(g) → 2HCl(g) + I2(s)The experimentally determined rate law is rate = k[ICl][H2]. Write a two-step mechanism for this reaction using only bimolecular elementary reactions and show that it is consistent with the experimental rate law. (Hint: HI is an intermediate.)
Answer:
This mechanism is consistent with the experimental rate law if the first step is the rate-determining step.
Exercise B
The reaction between NO and H2 occurs via a three-step process:
Write the rate law for each elementary reaction, write the balanced chemical equation for the overall reaction, and identify the rate-determining step. Is the rate law for the rate-determining step consistent with the experimentally derived rate law for the overall reaction: rate = k[NO]2[H2]2?
Answer:
- rate = k1[NO]2;
- rate = k2[N2O2][H2];
- rate = k3[N2O][H2];
- 2NO(g) + 2H2(g) → N2(g) + 2H2O(g)
- step 2
- Yes, because the rate of formation of [N2O2] = k1[NO]2. Substituting k1[NO]2 for [N2O2] in the rate law for step 2 gives the experimentally derived rate law for the overall chemical reaction, where k = k1k2.
Chain Reactions
Many reaction mechanisms, like those discussed so far, consist of only two or three elementary reactions. Many others consist of long series of elementary reactions. The most common mechanisms are chain reactionsA reaction mechanism in which one or more elementary reactions that contain a highly reactive species repeat again and again during the reaction process., in which one or more elementary reactions that contain a highly reactive species repeat again and again during the reaction process. Chain reactions occur in fuel combustion, explosions, the formation of many polymers, and the tissue changes associated with aging. They are also important in the chemistry of the atmosphere.
Chain reactions are described as having three stages. The first is initiation, a step that produces one or more reactive intermediates. Often these intermediates are radicalsSpecies that have one or more unpaired valence electrons., species that have an unpaired valence electron. In the second stage, propagation, reactive intermediates are continuously consumed and regenerated while products are formed. Intermediates are also consumed but not regenerated in the final stage of a chain reaction, termination, usually by forming stable products.
Let us look at the reaction of methane with chlorine at elevated temperatures (400°C–450°C), a chain reaction used in industry to manufacture methyl chloride (CH3Cl), dichloromethane (CH2Cl2), chloroform (CHCl3), and carbon tetrachloride (CCl4):
CH4 + Cl2 → CH3Cl + HCl CH3Cl + Cl2 → CH2Cl2 + HCl CH2Cl2 + Cl2 → CHCl3 + HCl CHCl3 + Cl2 → CCl4 + HClDirect chlorination generally produces a mixture of all four carbon-containing products, which must then be separated by distillation. In our discussion, we will examine only the chain reactions that lead to the preparation of CH3Cl.
In the initiation stage of this reaction, the relatively weak Cl–Cl bond cleaves at temperatures of about 400°C to produce chlorine atoms (Cl·):
Cl2 → 2Cl·During propagation, a chlorine atom removes a hydrogen atom from a methane molecule to give HCl and CH3·, the methyl radical:
Cl· + CH4 → CH3· + HClThe methyl radical then reacts with a chlorine molecule to form methyl chloride and another chlorine atom, Cl·:
CH3· + Cl2 → CH3Cl + Cl·The sum of the propagation reactions is the same as the overall balanced chemical equation for the reaction:
Without a chain-terminating reaction, propagation reactions would continue until either the methane or the chlorine was consumed. Because radical species react rapidly with almost anything, however, including each other, they eventually form neutral compounds, thus terminating the chain reaction in any of three ways:
CH3· + Cl· → CH3Cl CH3· + CH3· → H3CCH3 Cl· + Cl· → Cl2Here is the overall chain reaction, with the desired product (CH3Cl) in bold:
| Initiation: | Cl2 → 2Cl· |
| Propagation: | Cl· + CH4 → CH3· + HCl |
| CH3· + Cl2 → CH3Cl + Cl· | |
| Termination: | CH3· + Cl· → CH3Cl |
| CH3· + CH3· → H3CCH3 | |
| Cl· + Cl· → Cl2 |
The chain reactions responsible for explosions generally have an additional feature: the existence of one or more chain branching steps, in which one radical reacts to produce two or more radicals, each of which can then go on to start a new chain reaction. Repetition of the branching step has a cascade effect such that a single initiation step generates large numbers of chain reactions. The result is a very rapid reaction or an explosion.
The reaction of H2 and O2, used to propel rockets, is an example of a chain branching reaction:
| Initiation: | H2 + O2 → HO2· + H· |
| Propagation: | HO2· + H2 → H2O + OH· |
| OH· + H2 → H2O + H· | |
| Termination: | H· + O2 → OH· + ·O· |
| ·O· + H2 → OH· + H· |
Termination reactions occur when the extraordinarily reactive H· or OH· radicals react with a third species. The complexity of a chain reaction makes it unfeasible to write a rate law for the overall reaction.
Summary
A reaction mechanism is the microscopic path by which reactants are transformed into products. Each step is an elementary reaction. Species that are formed in one step and consumed in another are intermediates. Each elementary reaction can be described in terms of its molecularity, the number of molecules that collide in that step. The slowest step in a reaction mechanism is the rate-determining step. Chain reactions consist of three kinds of reactions: initiation, propagation, and termination. Intermediates in chain reactions are often radicals, species that have an unpaired valence electron.
Key Takeaway
- A balanced chemical reaction does not necessarily reveal either the individual elementary reactions by which a reaction occurs or its rate law.
Conceptual Problems
-
How does the term molecularity relate to elementary reactions? How does it relate to the overall balanced chemical equation?
-
What is the relationship between the reaction order and the molecularity of a reaction? What is the relationship between the reaction order and the balanced chemical equation?
-
When you determine the rate law for a given reaction, why is it valid to assume that the concentration of an intermediate does not change with time during the course of the reaction?
-
If you know the rate law for an overall reaction, how would you determine which elementary reaction is rate determining? If an intermediate is contained in the rate-determining step, how can the experimentally determined rate law for the reaction be derived from this step?
-
Give the rate-determining step for each case.
- Traffic is backed up on a highway because two lanes merge into one.
- Gas flows from a pressurized cylinder fitted with a gas regulator and then is bubbled through a solution.
- A document containing text and graphics is downloaded from the Internet.
-
Before being sent on an assignment, an aging James Bond was sent off to a health farm where part of the program’s focus was to purge his body of radicals. Why was this goal considered important to his health?
Numerical Problems
-
Cyclopropane, a mild anesthetic, rearranges to propylene via a collision that produces and destroys an energized species. The important steps in this rearrangement are as follows:
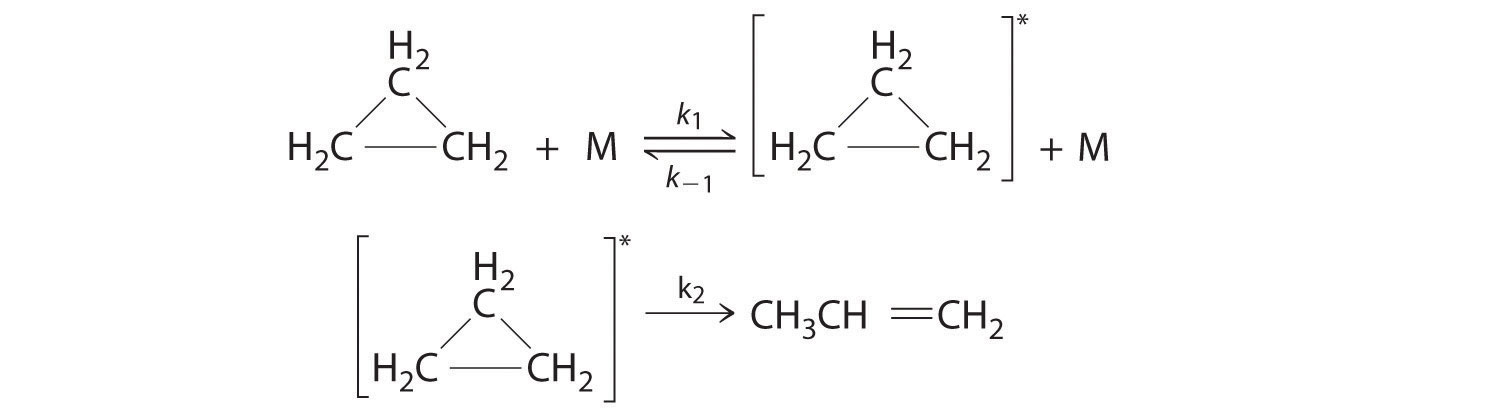
where M is any molecule, including cyclopropane. Only those cyclopropane molecules with sufficient energy (denoted with an asterisk) can rearrange to propylene. Which step determines the rate constant of the overall reaction?
-
Above approximately 500 K, the reaction between NO2 and CO to produce CO2 and NO follows the second-order rate law Δ[CO2]/Δt = k[NO2][CO]. At lower temperatures, however, the rate law is Δ[CO2]/Δt = k′[NO2]2, for which it is known that NO3 is an intermediate in the mechanism. Propose a complete low-temperature mechanism for the reaction based on this rate law. Which step is the slowest?
-
Nitramide (O2NNH2) decomposes in aqueous solution to N2O and H2O. What is the experimental rate law (Δ[N2O]/Δt) for the decomposition of nitramide if the mechanism for the decomposition is as follows?
Assume that the rates of the forward and reverse reactions in the first equation are equal.
-
The following reactions are given:
What is the relationship between the relative magnitudes of k−1 and k2 if these reactions have the rate law Δ[F]/Δt = k[A][B][E]/[C]? How does the magnitude of k1 compare to that of k2? Under what conditions would you expect the rate law to be Δ[F]/Δt = k′[A][B]? Assume that the rates of the forward and reverse reactions in the first equation are equal.
Answers
-
The k2 step is likely to be rate limiting; the rate cannot proceed any faster than the second step.
-
-
-
14.7 The Collision Model of Chemical Kinetics
Learning Objective
- To understand why and how chemical reactions occur.
In Section 14.6 "Reaction Rates—A Microscopic View", you saw that it is possible to use kinetics studies of a chemical system, such as the effect of changes in reactant concentrations, to deduce events that occur on a microscopic scale, such as collisions between individual particles. Such studies have led to the collision model of chemical kinetics, which is a useful tool for understanding the behavior of reacting chemical species. According to the collision model, a chemical reaction can occur only when the reactant molecules, atoms, or ions collide with more than a certain amount of kinetic energy and in the proper orientation. The collision model explains why, for example, most collisions between molecules do not result in a chemical reaction. Nitrogen and oxygen molecules in a single liter of air at room temperature and 1 atm of pressure collide about 1030 times per second. If every collision produced two molecules of NO, the atmosphere would have been converted to NO and then NO2 a long time ago. Instead, in most collisions, the molecules simply bounce off one another without reacting, much as marbles bounce off each other when they collide. The collision model also explains why such chemical reactions occur more rapidly at higher temperatures. For example, the reaction rates of many reactions that occur at room temperature approximately double with a temperature increase of only 10°C. In this section, we will use the collision model to analyze this relationship between temperature and reaction rates.
Activation Energy
In Chapter 10 "Gases", we discussed the kinetic molecular theory of gases, which showed that the average kinetic energy of the particles of a gas increases with increasing temperature. Because the speed of a particle is proportional to the square root of its kinetic energy, increasing the temperature will also increase the number of collisions between molecules per unit time. What the kinetic molecular theory of gases does not explain is why the reaction rate of most reactions approximately doubles with a 10°C temperature increase. This result is surprisingly large considering that a 10°C increase in the temperature of a gas from 300 K to 310 K increases the kinetic energy of the particles by only about 4%, leading to an increase in molecular speed of only about 2% and a correspondingly small increase in the number of bimolecular collisions per unit time.
The collision model of chemical kinetics explains this behavior by introducing the concept of activation energy (Ea)The energy barrier or threshold that corresponds to the minimum amount of energy the particles in a reaction must have to react when they colllide.. We will define this concept using the reaction of NO with ozone, which plays an important role in the depletion of ozone in the ozone layer:
Equation 14.37
NO(g) + O3(g) → NO2(g) + O2(g)Increasing the temperature from 200 K to 350 K causes the rate constant for this particular reaction to increase by a factor of more than 10, whereas the increase in the frequency of bimolecular collisions over this temperature range is only 30%. Thus something other than an increase in the collision rate must be affecting the reaction rate.
The reaction rate, not the rate constant, will vary with concentration. The rate constant, however, does vary with temperature. Figure 14.20 "Rate Constant versus Temperature for the Reaction of NO with O" shows a plot of the rate constant of the reaction of NO with O3 at various temperatures. The relationship is not linear but instead resembles the relationships seen in graphs of vapor pressure versus temperature (Chapter 11 "Liquids") and of conductivity versus temperature (Chapter 12 "Solids"). In all three cases, the shape of the plots results from a distribution of kinetic energy over a population of particles (electrons in the case of conductivity; molecules in the case of vapor pressure; and molecules, atoms, or ions in the case of reaction rates). Only a fraction of the particles have sufficient energy to overcome an energy barrier.
Figure 14.20 Rate Constant versus Temperature for the Reaction of NO with O3
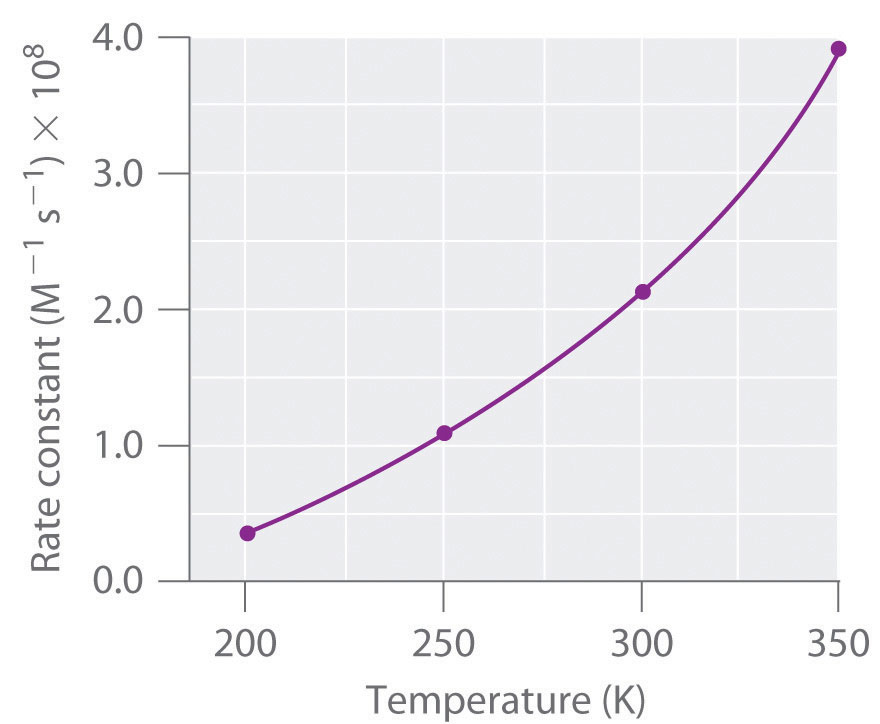
The nonlinear shape of the curve is caused by a distribution of kinetic energy over a population of molecules. Only a fraction of the particles have enough energy to overcome an energy barrier, but as the temperature is increased, the size of that fraction increases.
In the case of vapor pressure, particles must overcome an energy barrier to escape from the liquid phase to the gas phase. This barrier corresponds to the energy of the intermolecular forces that hold the molecules together in the liquid. In conductivity, the barrier is the energy gap between the filled and empty bands. In chemical reactions, the energy barrier corresponds to the amount of energy the particles must have to react when they collide. This energy threshold, called the activation energy, was first postulated in 1888 by the Swedish chemist Svante Arrhenius (1859–1927; Nobel Prize in Chemistry 1903). It is the minimum amount of energy needed for a reaction to occur. Reacting molecules must have enough energy to overcome electrostatic repulsion, and a minimum amount of energy is required to break chemical bonds so that new ones may be formed. Molecules that collide with less than the threshold energy bounce off one another chemically unchanged, with only their direction of travel and their speed altered by the collision. Molecules that are able to overcome the energy barrier are able to react and form an arrangement of atoms called the activated complexAlso called the transition state, the arrangement of atoms that first forms when molecules are able to overcome the activation energy and react. or the transition stateAlso called the activated complex, the arrangement of atoms that first forms when molecules are able to overcome the activation energy and react. of the reaction. The activated complex is not a reaction intermediate; it does not last long enough to be detected readily.
Note the Pattern
Any phenomenon that depends on the distribution of thermal energy in a population of particles has a nonlinear temperature dependence.
Graphing Energy Changes during a Reaction
We can graph the energy of a reaction by plotting the potential energy of the system as the reaction progresses. Figure 14.21 "Energy of the Activated Complex for the NO–O" shows a plot for the NO–O3 system, in which the vertical axis is potential energy and the horizontal axis is the reaction coordinate, which indicates the progress of the reaction with time. The activated complex is shown in brackets with an asterisk. The overall change in potential energy for the reaction (ΔE) is negative, which means that the reaction releases energy. (In this case, ΔE is −200.8 kJ/mol.) To react, however, the molecules must overcome the energy barrier to reaction (Ea is 9.6 kJ/mol). That is, 9.6 kJ/mol must be put into the system as the activation energy. Below this threshold, the particles do not have enough energy for the reaction to occur.
Figure 14.21 Energy of the Activated Complex for the NO–O3 System
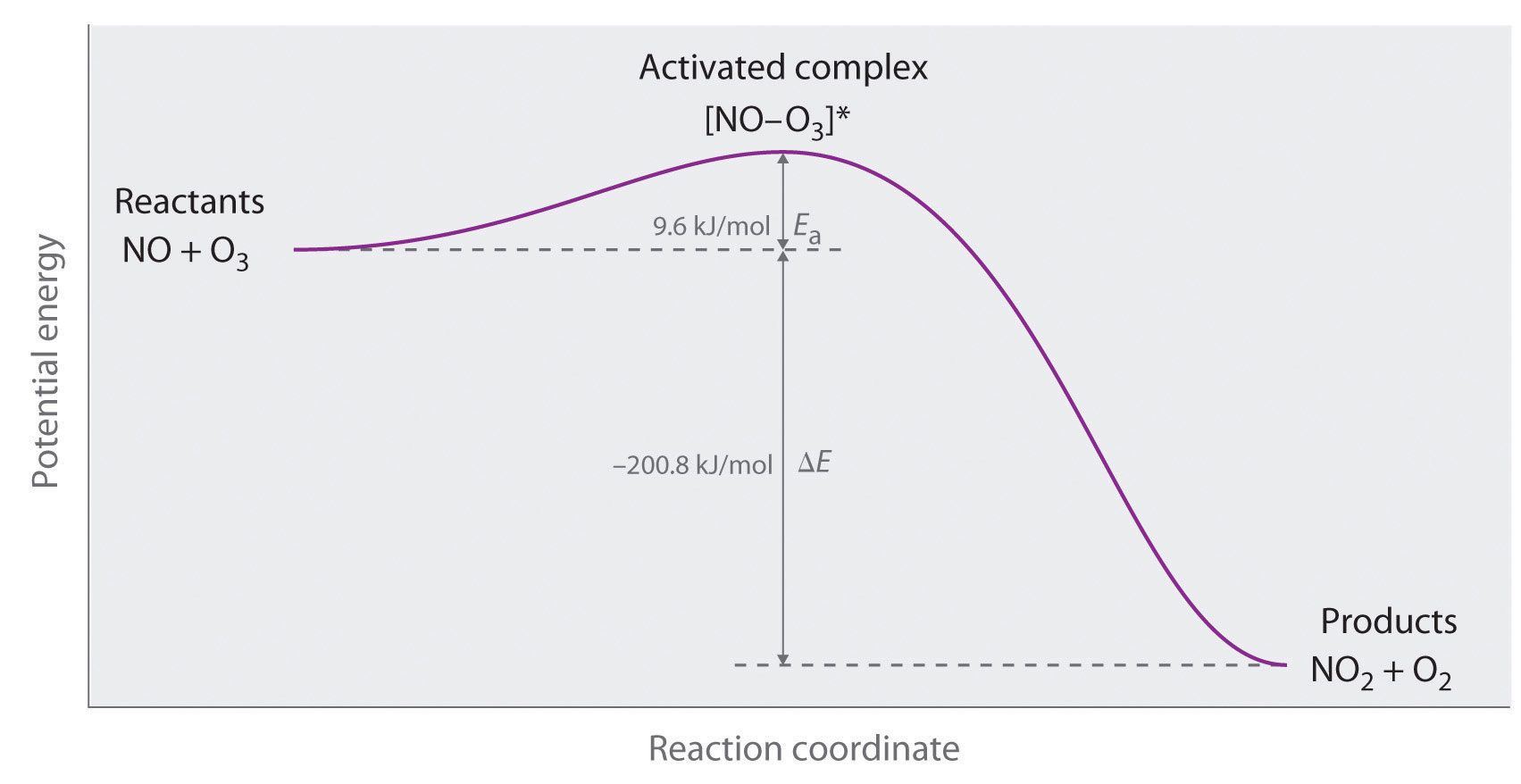
The diagram shows how the energy of this system varies as the reaction proceeds from reactants to products. Note the initial increase in energy required to form the activated complex.
Part (a) in Figure 14.22 "Differentiating between " illustrates the general situation in which the products have a lower potential energy than the reactants. In contrast, part (b) in Figure 14.22 "Differentiating between " illustrates the case in which the products have a higher potential energy than the reactants, so the overall reaction requires an input of energy; that is, it is energetically uphill, and ΔE > 0. Although the energy changes that result from a reaction can be positive, negative, or even zero, in all cases an energy barrier must be overcome before a reaction can occur. This means that the activation energy is always positive.
Figure 14.22 Differentiating between Ea and ΔE
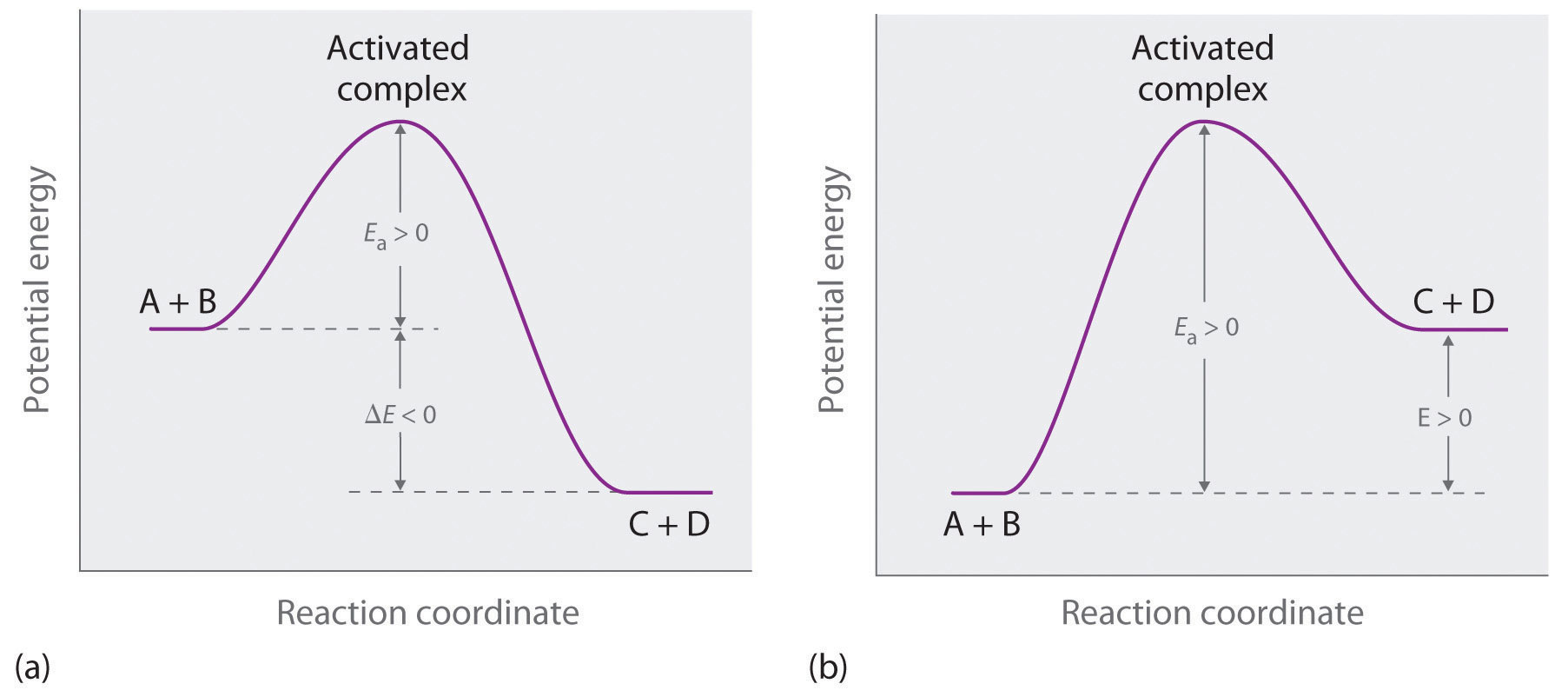
The potential energy diagrams for a reaction with (a) ΔE < 0 and (b) ΔE > 0 illustrate the change in the potential energy of the system as reactants are converted to products. Ea is always positive. For a reaction such as the one shown in (b), Ea must be greater than ΔE.
Note the Pattern
For similar reactions under comparable conditions, the one with the smallest Ea will occur most rapidly.
Whereas ΔE is related to the tendency of a reaction to occur spontaneously, Ea gives us information about the reaction rate and how rapidly the reaction rate changes with temperature. (For more information on spontaneous reactions, see Chapter 18 "Chemical Thermodynamics".) For two similar reactions under comparable conditions, the reaction with the smallest Ea will occur more rapidly.
Even when the energy of collisions between two reactant species is greater than Ea, however, most collisions do not produce a reaction. The probability of a reaction occurring depends not only on the collision energy but also on the spatial orientation of the molecules when they collide. For NO and O3 to produce NO2 and O2, a terminal oxygen atom of O3 must collide with the nitrogen atom of NO at an angle that allows O3 to transfer an oxygen atom to NO to produce NO2 (Figure 14.23 "The Effect of Molecular Orientation on the Reaction of NO and O"). All other collisions produce no reaction. Because fewer than 1% of all possible orientations of NO and O3 result in a reaction at kinetic energies greater than Ea, most collisions of NO and O3 are unproductive. The fraction of orientations that result in a reaction is called the steric factor (p)The fraction of orientations of particles that result in a chemical reaction., and, in general, its value can range from 0 (no orientations of molecules result in reaction) to 1 (all orientations result in reaction).
Figure 14.23 The Effect of Molecular Orientation on the Reaction of NO and O3
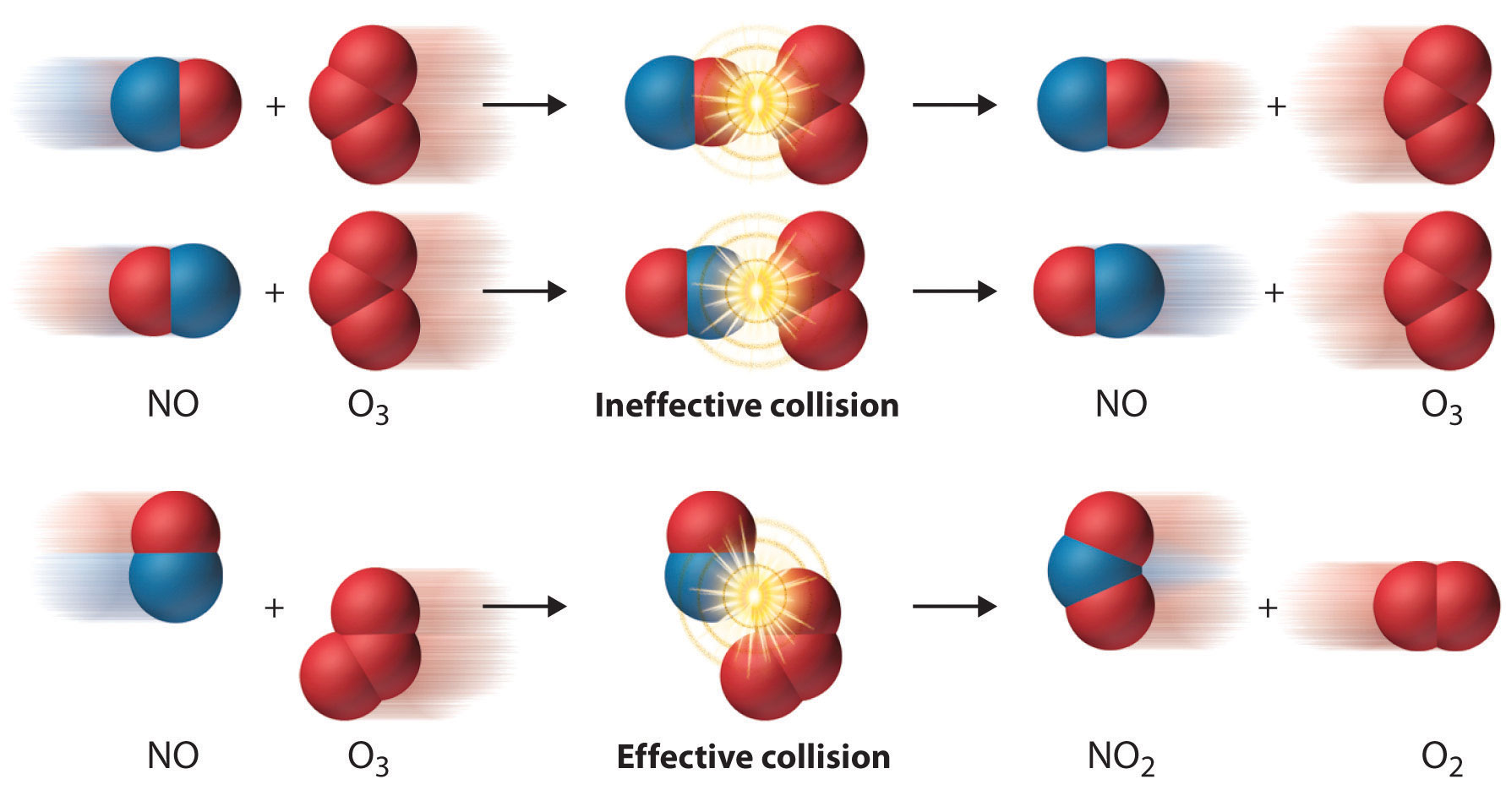
Most collisions of NO and O3 molecules occur with an incorrect orientation for a reaction to occur. Only those collisions in which the N atom of NO collides with one of the terminal O atoms of O3 are likely to produce NO2 and O2, even if the molecules collide with E > Ea.
The Arrhenius Equation
Figure 14.24 "Surmounting the Energy Barrier to a Reaction" shows both the kinetic energy distributions and a potential energy diagram for a reaction. The shaded areas show that at the lower temperature (300 K), only a small fraction of molecules collide with kinetic energy greater than Ea; however, at the higher temperature (500 K) a much larger fraction of molecules collide with kinetic energy greater than Ea. Consequently, the reaction rate is much slower at the lower temperature because only a relatively few molecules collide with enough energy to overcome the potential energy barrier.
Figure 14.24 Surmounting the Energy Barrier to a Reaction
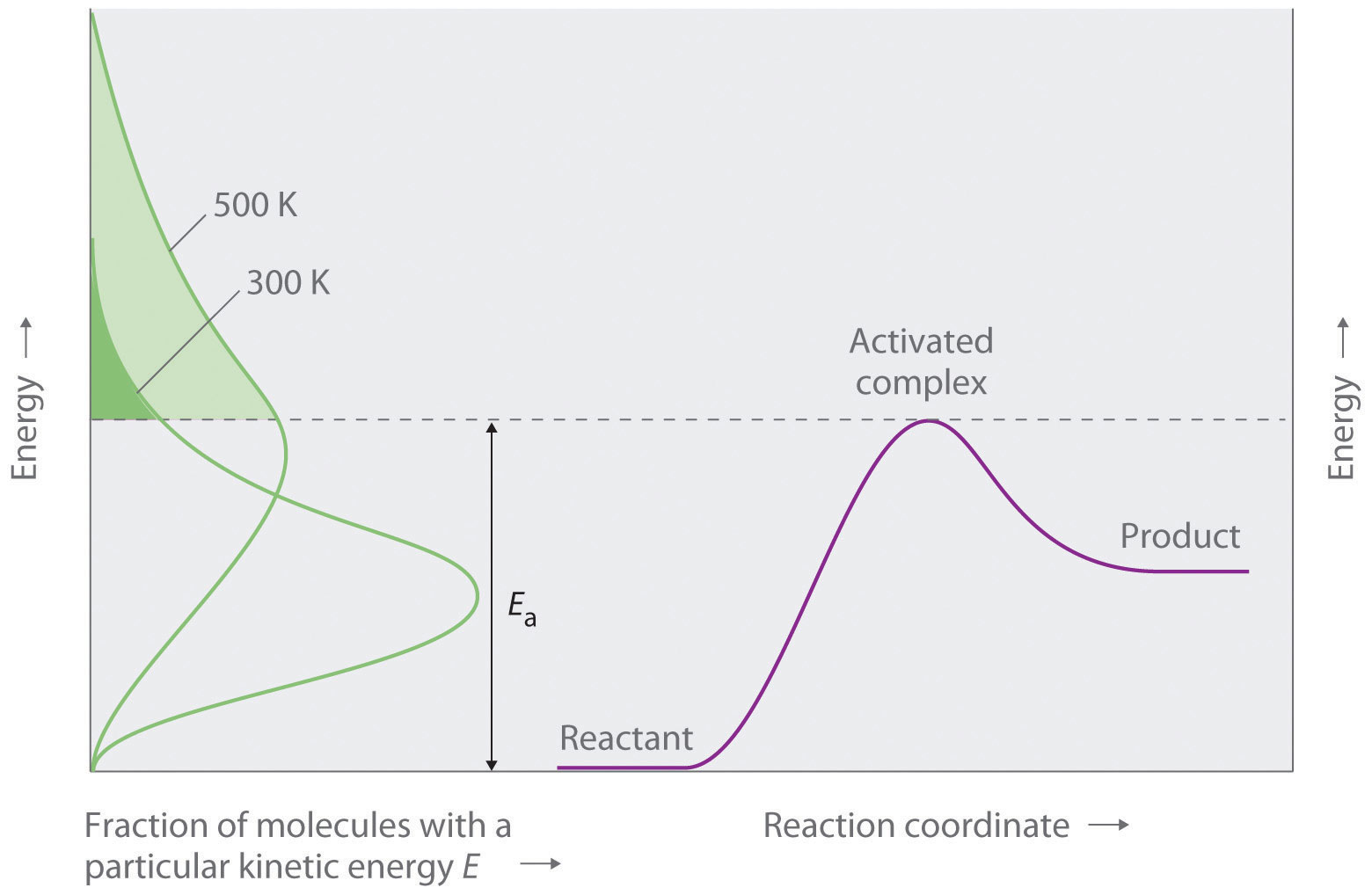
This chart juxtaposes the energy distributions of lower-temperature (300 K) and higher-temperature (500 K) samples of a gas against the potential energy diagram for a reaction. Only those molecules in the shaded region of the energy distribution curve have E > Ea and are therefore able to cross the energy barrier separating reactants and products. The fraction of molecules with E > Ea is much greater at 500 K than at 300 K, so the reaction will occur much more rapidly at 500 K.
For an A + B elementary reaction, all the factors that affect the reaction rate can be summarized in a single series of relationships:
rate = (collision frequency)(steric factor)(fraction of collisions with E > Ea)where
Equation 14.38
rate = k[A][B]Arrhenius used these relationships to arrive at an equation that relates the magnitude of the rate constant for a reaction to the temperature, the activation energy, and the constant, A, called the frequency factorA constant in the Arrhenius equation, it converts concentrations to collisions per second.:
Equation 14.39
The frequency factor is used to convert concentrations to collisions per second.Because the frequency of collisions depends on the temperature, A is actually not constant. Instead, A increases slightly with temperature as the increased kinetic energy of molecules at higher temperatures causes them to move slightly faster and thus undergo more collisions per unit time. Equation 14.39 is known as the Arrhenius equationAn expression that summarizes the collision model of chemical kinetics: and summarizes the collision model of chemical kinetics, where T is the absolute temperature (in K) and R is the ideal gas constant [8.314 J/(K·mol)]. Ea indicates the sensitivity of the reaction to changes in temperature. The reaction rate with a large Ea increases rapidly with increasing temperature, whereas the reaction rate with a smaller Ea increases much more slowly with increasing temperature.
If we know the reaction rate at various temperatures, we can use the Arrhenius equation to calculate the activation energy. Taking the natural logarithm of both sides of Equation 14.39,
Equation 14.40
Equation 14.40 is the equation of a straight line, y = mx + b, where y = ln k and x = 1/T. This means that a plot of ln k versus 1/T is a straight line with a slope of −Ea/R and an intercept of ln A. In fact, we need to measure the reaction rate at only two temperatures to estimate Ea.
Knowing the Ea at one temperature allows us to predict the reaction rate at other temperatures. This is important in cooking and food preservation, for example, as well as in controlling industrial reactions to prevent potential disasters. The procedure for determining Ea from reaction rates measured at several temperatures is illustrated in Example 13.
Example 13
Many people believe that the rate of a tree cricket’s chirping is related to temperature. To see whether this is true, biologists have carried out accurate measurements of the rate of tree cricket chirping (f) as a function of temperature (T). Use the data in the following table, along with the graph of ln[chirping rate] versus 1/T in Figure 14.25 "Graphical Determination of ", to calculate Ea for the biochemical reaction that controls cricket chirping. Then predict the chirping rate on a very hot evening, when the temperature is 308 K (35°C, or 95°F).
| Frequency (f; chirps/min) | ln f | T (K) | 1/T (K) |
|---|---|---|---|
| 200 | 5.30 | 299 | 3.34 × 10−3 |
| 179 | 5.19 | 298 | 3.36 × 10−3 |
| 158 | 5.06 | 296 | 3.38 × 10−3 |
| 141 | 4.95 | 294 | 3.40 × 10−3 |
| 126 | 4.84 | 293 | 3.41 × 10−3 |
| 112 | 4.72 | 292 | 3.42 × 10−3 |
| 100 | 4.61 | 290 | 3.45 × 10−3 |
| 89 | 4.49 | 289 | 3.46 × 10−3 |
| 79 | 4.37 | 287 | 3.48 × 10−3 |
Given: chirping rate at various temperatures
Asked for: activation energy and chirping rate at specified temperature
Strategy:
A From the plot of ln f versus 1/T in Figure 14.25 "Graphical Determination of ", calculate the slope of the line (−Ea/R) and then solve for the activation energy.
B Express Equation 14.40 in terms of k1 and T1 and then in terms of k2 and T2.
C Subtract the two equations; rearrange the result to describe k2/k1 in terms of T2 and T1.
D Using measured data from the table, solve the equation to obtain the ratio k2/k1. Using the value listed in the table for k1, solve for k2.
Solution:
A If cricket chirping is controlled by a reaction that obeys the Arrhenius equation, then a plot of ln f versus 1/T should give a straight line (Figure 14.25 "Graphical Determination of "). Also, the slope of the plot of ln f versus 1/T should be equal to −Ea/R. We can use the two endpoints in Figure 14.25 "Graphical Determination of " to estimate the slope:
A computer best-fit line through all the points has a slope of −6.67 × 103 K, so our estimate is very close. We now use it to solve for the activation energy:
B If the activation energy of a reaction and the rate constant at one temperature are known, then we can calculate the reaction rate at any other temperature. We can use Equation 14.40 to express the known rate constant (k1) at the first temperature (T1) as follows:
Similarly, we can express the unknown rate constant (k2) at the second temperature (T2) as follows:
C These two equations contain four known quantities (Ea, T1, T2, and k1) and two unknowns (A and k2). We can eliminate A by subtracting the first equation from the second:
Then
D To obtain the best prediction of chirping rate at 308 K (T2), we try to choose for T1 and k1 the measured rate constant and corresponding temperature in the data table that is closest to the best-fit line in the graph. Choosing data for T1 = 296 K, where f = 158, and using the Ea calculated previously,
Thus k308/k296 = 2.4 and k308 = (2.4)(158) = 380, and the chirping rate on a night when the temperature is 308 K is predicted to be 380 chirps per minute.
Exercise
The equation for the decomposition of NO2 to NO and O2 is second order in NO2:
2NO2(g) → 2NO(g) + O2(g)Data for the reaction rate as a function of temperature are listed in the following table. Calculate Ea for the reaction and the rate constant at 700 K.
| T (K) | k (M−1·s−1) |
|---|---|
| 592 | 522 |
| 603 | 755 |
| 627 | 1700 |
| 652 | 4020 |
| 656 | 5030 |
Answer: Ea = 114 kJ/mol; k700 = 18,600 M−1·s−1 = 1.86 × 104 M−1·s−1.
What Ea results in a doubling of the reaction rate with a 10°C increase in temperature from 20° to 30°C?
Answer: about 51 kJ/mol
Figure 14.25 Graphical Determination of Ea for Tree Cricket Chirping
When the natural logarithm of the rate of tree cricket chirping is plotted versus 1/T, a straight line results. The slope of the line suggests that the chirping rate is controlled by a single reaction with an Ea of 55 kJ/mol.
Summary
A minimum energy (activation energy, Ea) is required for a collision between molecules to result in a chemical reaction. Plots of potential energy for a system versus the reaction coordinate show an energy barrier that must be overcome for the reaction to occur. The arrangement of atoms at the highest point of this barrier is the activated complex, or transition state, of the reaction. At a given temperature, the higher the Ea, the slower the reaction. The fraction of orientations that result in a reaction is the steric factor. The frequency factor, steric factor, and activation energy are related to the rate constant in the Arrhenius equation: A plot of the natural logarithm of k versus 1/T is a straight line with a slope of −Ea/R.
Key Takeaway
- For a chemical reaction to occur, an energy threshold must be overcome, and the reacting species must also have the correct spatial orientation.
Conceptual Problems
-
Although an increase in temperature results in an increase in kinetic energy, this increase in kinetic energy is not sufficient to explain the relationship between temperature and reaction rates. How does the activation energy relate to the chemical kinetics of a reaction? Why does an increase in temperature increase the reaction rate despite the fact that the average kinetic energy is still less than the activation energy?
-
For any given reaction, what is the relationship between the activation energy and each of the following?
- electrostatic repulsions
- bond formation in the activated complex
- the nature of the activated complex
-
If you are concerned with whether a reaction will occur rapidly, why would you be more interested in knowing the magnitude of the activation energy than the change in potential energy for the reaction?
-
The product C in the reaction A + B → C + D can be separated easily from the reaction mixture. You have been given pure A and pure B and are told to determine the activation energy for this reaction to determine whether the reaction is suitable for the industrial synthesis of C. How would you do this? Why do you need to know the magnitude of the activation energy to make a decision about feasibility?
-
Above Ea, molecules collide with enough energy to overcome the energy barrier for a reaction. Is it possible for a reaction to occur at a temperature less than that needed to reach Ea? Explain your answer.
-
What is the relationship between A, Ea, and T? How does an increase in A affect the reaction rate?
-
Of two highly exothermic reactions with different values of Ea, which would need to be monitored more carefully: the one with the smaller value or the one with the higher value? Why?
Numerical Problems
-
What happens to the approximate rate of a reaction when the temperature of the reaction is increased from 20°C to 30°C? What happens to the reaction rate when the temperature is raised to 70°C? For a given reaction at room temperature (20°C), what is the shape of a plot of reaction rate versus temperature as the temperature is increased to 70°C?
-
Acetaldehyde, used in silvering mirrors and some perfumes, undergoes a second-order decomposition between 700 and 840 K. From the data in the following table, would you say that acetaldehyde follows the general rule that each 10 K increase in temperature doubles the reaction rate?
T (K) k (M−1·s−1) 720 0.024 740 0.051 760 0.105 800 0.519 -
Bromoethane reacts with hydroxide ion in water to produce ethanol. The activation energy for this reaction is 90 kJ/mol. If the reaction rate is 3.6 × 10−5 M/s at 25°C, what would the reaction rate be at the following temperatures?
- 15°C
- 30°C
- 45°C
-
An enzyme-catalyzed reaction has an activation energy of 15 kcal/mol. How would the value of the rate constant differ between 20°C and 30°C? If the enzyme reduced the Ea from 25 kcal/mol to 15 kcal/mol, by what factor has the enzyme increased the reaction rate at each temperature?
-
The data in the following table are the rate constants as a function of temperature for the dimerization of 1,3-butadiene. What is the activation energy for this reaction?
T (K) k (M−1·min−1) 529 1.4 560 3.7 600 25 645 82 -
The reaction rate at 25°C is 1.0 × 10−4 M/s. Increasing the temperature to 75°C causes the reaction rate to increase to 7.0 × 10−2 M/s. Estimate Ea for this process. If Ea were 25 kJ/mol and the reaction rate at 25°C is 1.0 × 10−4 M/s, what would be the reaction rate at 75°C?
Answers
-
The reaction rate will approximately double: 20°C to 30°C, the reaction rate increases by about 21 = 2; 20°C to 70°C, the reaction rate increases by about 25 = 32-fold. A plot of reaction rate versus temperature will give an exponential increase: rate ∝ 2ΔT/10.
-
-
- 1.0 × 10−5 M/s
- 6.6 × 10−5 M/s
- 3.5 × 10−4 M/s
-
-
100 kJ/mol
-
14.8 Catalysis
Learning Objective
- To understand how catalysts increase the reaction rate and the selectivity of chemical reactions.
Chapter 3 "Chemical Reactions" described catalystsA substance that participates in a reaction and causes it to occur more rapidly but that can be recovered unchanged at the end of the reaction and reused. Catalysts may also control which products are formed in a reaction. as substances that increase the reaction rate of a chemical reaction without being consumed in the process. A catalyst, therefore, does not appear in the overall stoichiometry of the reaction it catalyzes, but it must appear in at least one of the elementary reactions in the mechanism for the catalyzed reaction. The catalyzed pathway has a lower Ea, but the net change in energy that results from the reaction (the difference between the energy of the reactants and the energy of the products) is not affected by the presence of a catalyst (Figure 14.26 "Lowering the Activation Energy of a Reaction by a Catalyst"). Nevertheless, because of its lower Ea, the reaction rate of a catalyzed reaction is faster than the reaction rate of the uncatalyzed reaction at the same temperature. Because a catalyst decreases the height of the energy barrier, its presence increases the reaction rates of both the forward and the reverse reactions by the same amount. In this section, we will examine the three major classes of catalysts: heterogeneous catalysts, homogeneous catalysts, and enzymes.
Note the Pattern
A catalyst affects Ea, not ΔE.
Figure 14.26 Lowering the Activation Energy of a Reaction by a Catalyst
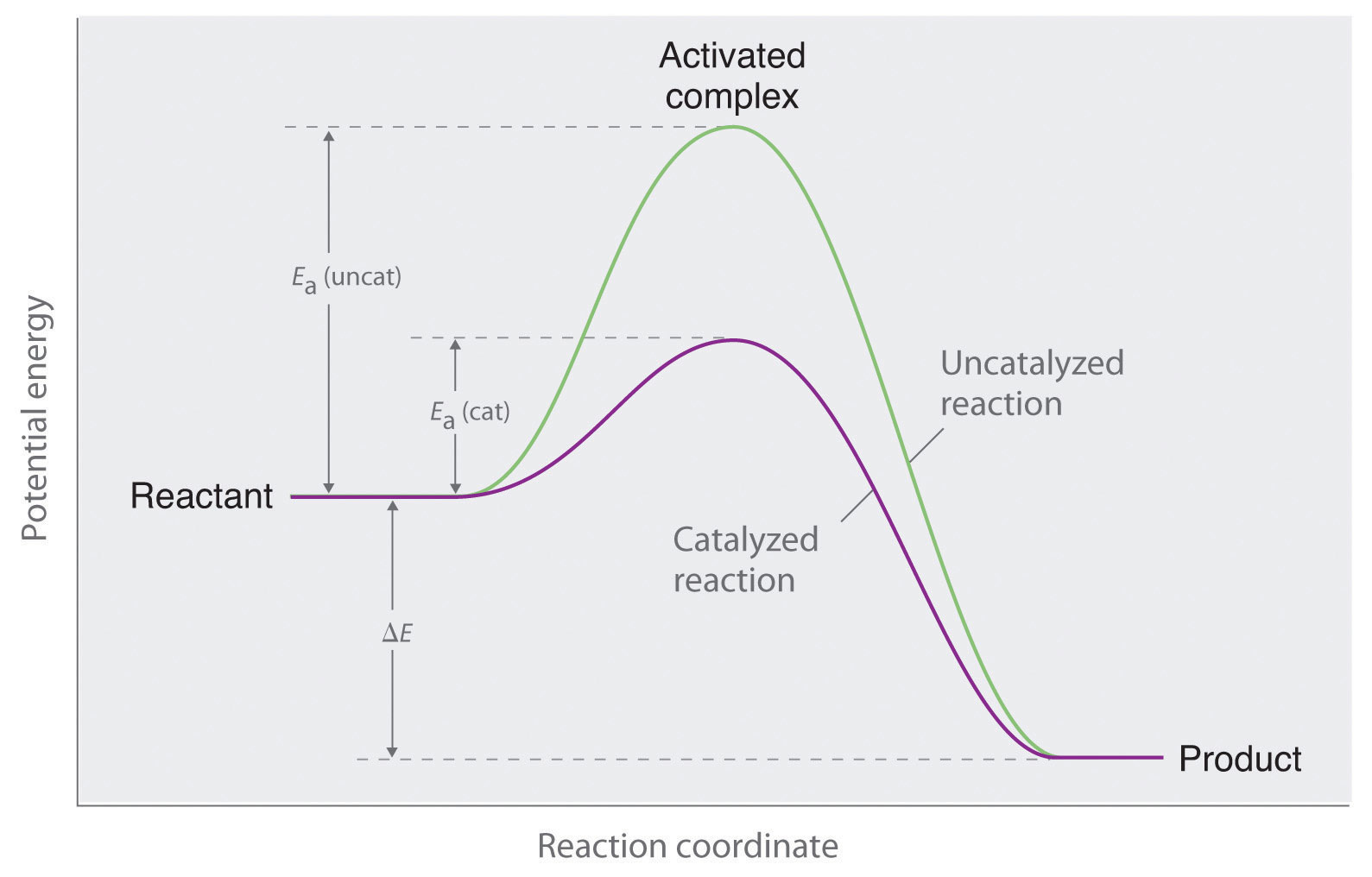
This graph compares potential energy diagrams for a single-step reaction in the presence and absence of a catalyst. The only effect of the catalyst is to lower the activation energy of the reaction. The catalyst does not affect the energy of the reactants or products (and thus does not affect ΔE).
Heterogeneous Catalysis
In heterogeneous catalysisA catalytic reaction in which the catalyst is in a different phase from the reactants., the catalyst is in a different phase from the reactants. At least one of the reactants interacts with the solid surface in a physical process called adsorption in such a way that a chemical bond in the reactant becomes weak and then breaks. Poisons are substances that bind irreversibly to catalysts, preventing reactants from adsorbing and thus reducing or destroying the catalyst’s efficiency.
An example of heterogeneous catalysis is the interaction of hydrogen gas with the surface of a metal, such as Ni, Pd, or Pt. As shown in part (a) in Figure 14.27 "Hydrogenation of Ethylene on a Heterogeneous Catalyst", the hydrogen–hydrogen bonds break and produce individual adsorbed hydrogen atoms on the surface of the metal. Because the adsorbed atoms can move around on the surface, two hydrogen atoms can collide and form a molecule of hydrogen gas that can then leave the surface in the reverse process, called desorption. Adsorbed H atoms on a metal surface are substantially more reactive than a hydrogen molecule. Because the relatively strong H–H bond (dissociation energy = 432 kJ/mol) has already been broken, the energy barrier for most reactions of H2 is substantially lower on the catalyst surface.
Figure 14.27 Hydrogenation of Ethylene on a Heterogeneous Catalyst
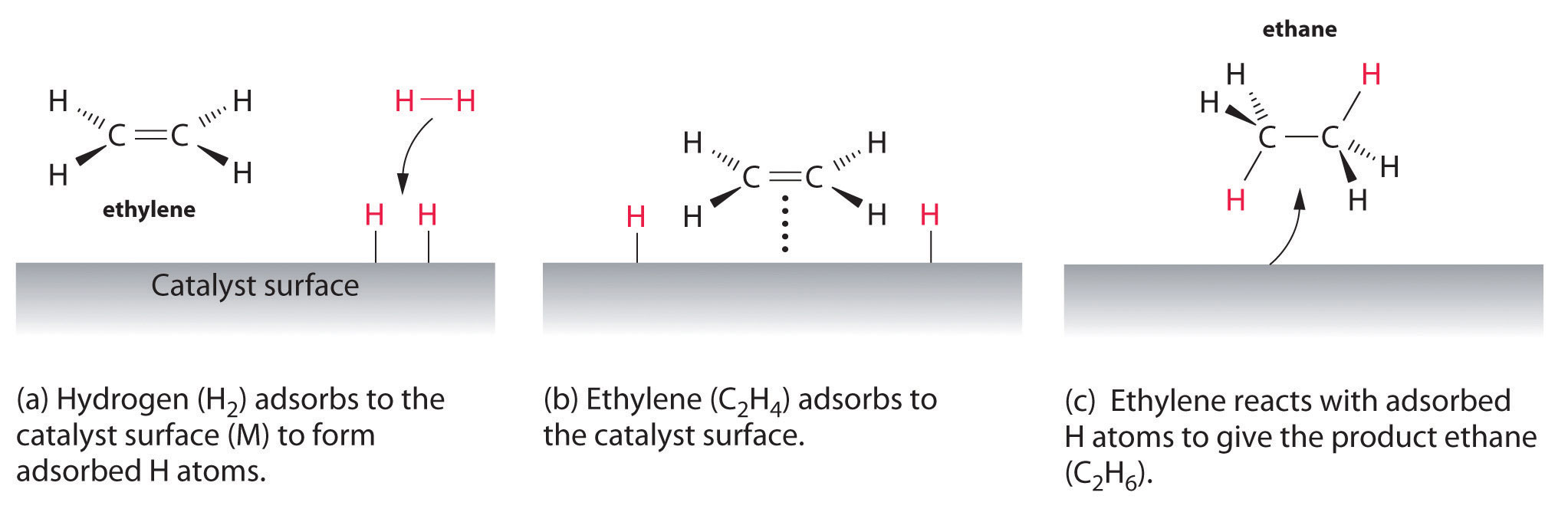
When a molecule of hydrogen adsorbs to the catalyst surface, the H–H bond breaks, and new M–H bonds are formed. The individual H atoms are more reactive than gaseous H2. When a molecule of ethylene interacts with the catalyst surface, it reacts with the H atoms in a stepwise process to eventually produce ethane, which is released.
Figure 14.27 "Hydrogenation of Ethylene on a Heterogeneous Catalyst" shows a process called hydrogenation, in which hydrogen atoms are added to the double bond of an alkene, such as ethylene, to give a product that contains C–C single bonds, in this case ethane. Hydrogenation is used in the food industry to convert vegetable oils, which consist of long chains of alkenes, to more commercially valuable solid derivatives that contain alkyl chains. Hydrogenation of some of the double bonds in polyunsaturated vegetable oils, for example, produces margarine, a product with a melting point, texture, and other physical properties similar to those of butter.
Several important examples of industrial heterogeneous catalytic reactions are in Table 14.8 "Some Commercially Important Reactions that Employ Heterogeneous Catalysts". Although the mechanisms of these reactions are considerably more complex than the simple hydrogenation reaction described here, they all involve adsorption of the reactants onto a solid catalytic surface, chemical reaction of the adsorbed species (sometimes via a number of intermediate species), and finally desorption of the products from the surface.
Table 14.8 Some Commercially Important Reactions that Employ Heterogeneous Catalysts
| Commercial Process | Catalyst | Initial Reaction | Final Commercial Product |
|---|---|---|---|
| contact process | V2O5 or Pt | 2SO2 + O2 → 2SO3 | H2SO4 |
| Haber process | Fe, K2O, Al2O3 | N2 + 3H2 → 2NH3 | NH3 |
| Ostwald process | Pt and Rh | 4NH3 + 5O2 → 4NO + 6H2O | HNO3 |
| water–gas shift reaction | Fe, Cr2O3, or Cu | CO + H2O → CO2 + H2 | H2 for NH3, CH3OH, and other fuels |
| steam reforming | Ni | CH4 + H2O → CO + 3H2 | H2 |
| methanol synthesis | ZnO and Cr2O3 | CO + 2H2 → CH3OH | CH3OH |
| Sohio process | bismuth phosphomolybdate | ||
| catalytic hydrogenation | Ni, Pd, or Pt | RCH=CHR′ + H2 → RCH2—CH2R′ | partially hydrogenated oils for margarine, and so forth |
Homogeneous Catalysis
In homogeneous catalysisA catalytic reaction in which the catalyst is uniformly dispersed throughout the reactant mixture to form a solution., the catalyst is in the same phase as the reactant(s). The number of collisions between reactants and catalyst is at a maximum because the catalyst is uniformly dispersed throughout the reaction mixture. Many homogeneous catalysts in industry are transition metal compounds (Table 14.9 "Some Commercially Important Reactions that Employ Homogeneous Catalysts"), but recovering these expensive catalysts from solution has been a major challenge. As an added barrier to their widespread commercial use, many homogeneous catalysts can be used only at relatively low temperatures, and even then they tend to decompose slowly in solution. Despite these problems, a number of commercially viable processes have been developed in recent years. High-density polyethylene and polypropylene are produced by homogeneous catalysis.
Table 14.9 Some Commercially Important Reactions that Employ Homogeneous Catalysts
| Commercial Process | Catalyst | Reactants | Final Product |
|---|---|---|---|
| Union Carbide | [Rh(CO)2I2]− | CO + CH3OH | CH3CO2H |
| hydroperoxide process | Mo(VI) complexes | CH3CH=CH2 + R–O–O–H |
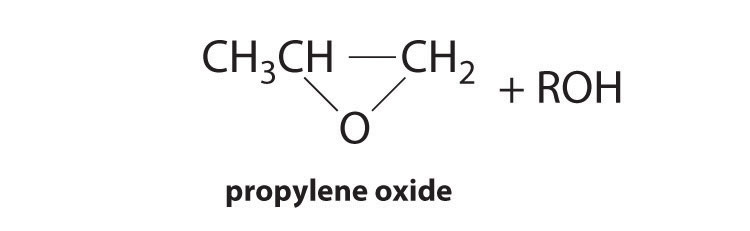
|
| hydroformylation | Rh/PR3 complexes | RCH=CH2 + CO + H2 | RCH2CH2CHO |
| adiponitrile process | Ni/PR3 complexes | 2HCN + CH2=CHCH=CH2 | NCCH2CH2CH2CH2CN used to synthesize nylon |
| olefin polymerization | (RC5H5)2ZrCl2 | CH2=CH2 | –(CH2CH2–)n: high-density polyethylene |
Enzymes
Enzymes, catalysts that occur naturally in living organisms, are almost all protein molecules with typical molecular masses of 20,000–100,000 amu. Some are homogeneous catalysts that react in aqueous solution within a cellular compartment of an organism. Others are heterogeneous catalysts embedded within the membranes that separate cells and cellular compartments from their surroundings. The reactant in an enzyme-catalyzed reaction is called a substrateThe reactant in an enzyme-catalyzed reaction..
Because enzymes can increase reaction rates by enormous factors (up to 1017 times the uncatalyzed rate) and tend to be very specific, typically producing only a single product in quantitative yield, they are the focus of active research. At the same time, enzymes are usually expensive to obtain, they often cease functioning at temperatures greater than 37°C, have limited stability in solution, and have such high specificity that they are confined to turning one particular set of reactants into one particular product. This means that separate processes using different enzymes must be developed for chemically similar reactions, which is time-consuming and expensive. Thus far, enzymes have found only limited industrial applications, although they are used as ingredients in laundry detergents, contact lens cleaners, and meat tenderizers. The enzymes in these applications tend to be proteases, which are able to cleave the amide bonds that hold amino acids together in proteins. Meat tenderizers, for example, contain a protease called papain, which is isolated from papaya juice. It cleaves some of the long, fibrous protein molecules that make inexpensive cuts of beef tough, producing a piece of meat that is more tender. Some insects, like the bombadier beetle, carry an enzyme capable of catalyzing the decomposition of hydrogen peroxide to water (Figure 14.28 "A Catalytic Defense Mechanism").
Enzyme inhibitorsSubstances that decrease the reaction rate of an enzyme-catalyzed reaction by binding to a specific portion of the enzyme, thus slowing or preventing a reaction from occurring. cause a decrease in the reaction rate of an enzyme-catalyzed reaction by binding to a specific portion of an enzyme and thus slowing or preventing a reaction from occurring. Irreversible inhibitors are therefore the equivalent of poisons in heterogeneous catalysis. One of the oldest and most widely used commercial enzyme inhibitors is aspirin, which selectively inhibits one of the enzymes involved in the synthesis of molecules that trigger inflammation. The design and synthesis of related molecules that are more effective, more selective, and less toxic than aspirin are important objectives of biomedical research.
Figure 14.28 A Catalytic Defense Mechanism

The scalding, foul-smelling spray emitted by this bombardier beetle is produced by the catalytic decomposition of H2O2.
Summary
Catalysts participate in a chemical reaction and increase its rate. They do not appear in the reaction’s net equation and are not consumed during the reaction. Catalysts allow a reaction to proceed via a pathway that has a lower activation energy than the uncatalyzed reaction. In heterogeneous catalysis, catalysts provide a surface to which reactants bind in a process of adsorption. In homogeneous catalysis, catalysts are in the same phase as the reactants. Enzymes are biological catalysts that produce large increases in reaction rates and tend to be specific for certain reactants and products. The reactant in an enzyme-catalyzed reaction is called a substrate. Enzyme inhibitors cause a decrease in the reaction rate of an enzyme-catalyzed reaction.
Key Takeaway
- Catalysts allow a reaction to proceed via a pathway that has a lower activation energy.
Conceptual Problems
-
What effect does a catalyst have on the activation energy of a reaction? What effect does it have on the frequency factor (A)? What effect does it have on the change in potential energy for the reaction?
-
How is it possible to affect the product distribution of a reaction by using a catalyst?
-
A heterogeneous catalyst works by interacting with a reactant in a process called adsorption. What occurs during this process? Explain how this can lower the activation energy.
-
What effect does increasing the surface area of a heterogeneous catalyst have on a reaction? Does increasing the surface area affect the activation energy? Explain your answer.
-
Identify the differences between a heterogeneous catalyst and a homogeneous catalyst in terms of the following.
- ease of recovery
- collision frequency
- temperature sensitivity
- cost
-
An area of intensive chemical research involves the development of homogeneous catalysts, even though homogeneous catalysts generally have a number of operational difficulties. Propose one or two reasons why a homogenous catalyst may be preferred.
-
Consider the following reaction between cerium(IV) and thallium(I) ions:
2Ce4+ + Tl+ → 2Ce3+ + Tl3+This reaction is slow, but Mn2+ catalyzes it, as shown in the following mechanism:
Ce4+ + Mn2+ → Ce3+ + Mn3+ Ce4+ + Mn3+ → Ce3+ + Mn4+ Mn4+ + Tl+ → Tl3+ + Mn2+In what way does Mn2+ increase the reaction rate?
-
The text identifies several factors that limit the industrial applications of enzymes. Still, there is keen interest in understanding how enzymes work for designing catalysts for industrial applications. Why?
-
Most enzymes have an optimal pH range; however, care must be taken when determining pH effects on enzyme activity. A decrease in activity could be due to the effects of changes in pH on groups at the catalytic center or to the effects on groups located elsewhere in the enzyme. Both examples are observed in chymotrypsin, a digestive enzyme that is a protease that hydrolyzes polypeptide chains. Explain how a change in pH could affect the catalytic activity due to (a) effects at the catalytic center and (b) effects elsewhere in the enzyme. (Hint: remember that enzymes are composed of functional amino acids.)
Answers
-
A catalyst lowers the activation energy of a reaction. Some catalysts can also orient the reactants and thereby increase the frequency factor. Catalysts have no effect on the change in potential energy for a reaction.
-
-
In adsorption, a reactant binds tightly to a surface. Because intermolecular interactions between the surface and the reactant weaken or break bonds in the reactant, its reactivity is increased, and the activation energy for a reaction is often decreased.
-
-
- Heterogeneous catalysts are easier to recover.
- Collision frequency is greater for homogeneous catalysts.
- Homogeneous catalysts are often more sensitive to temperature.
- Homogeneous catalysts are often more expensive.
-
-
The Mn2+ ion donates two electrons to Ce4+, one at a time, and then accepts two electrons from Tl+. Because Mn can exist in three oxidation states separated by one electron, it is able to couple one-electron and two-electron transfer reactions.
-
-
Numerical Problems
-
At some point during an enzymatic reaction, the concentration of the activated complex, called an enzyme–substrate complex (ES), and other intermediates involved in the reaction is nearly constant. When a single substrate is involved, the reaction can be represented by the following sequence of equations:
This can also be shown as follows:
Using molar concentrations and rate constants, write an expression for the rate of disappearance of the enzyme–substrate complex. Typically, enzyme concentrations are small, and substrate concentrations are high. If you were determining the rate law by varying the substrate concentrations under these conditions, what would be your apparent reaction order?
-
A particular reaction was found to proceed via the following mechanism:
A + B → C + D 2C → E E + A → 3B + FWhat is the overall reaction? Is this reaction catalytic, and if so, what species is the catalyst? Identify the intermediates.
-
A particular reaction has two accessible pathways (A and B), each of which favors conversion of X to a different product (Y and Z, respectively). Under uncatalyzed conditions pathway A is favored, but in the presence of a catalyst pathway B is favored. Pathway B is reversible, whereas pathway A is not. Which product is favored in the presence of a catalyst? without a catalyst? Draw a diagram illustrating what is occurring with and without the catalyst.
-
The kinetics of an enzyme-catalyzed reaction can be analyzed by plotting the reaction rate versus the substrate concentration. This type of analysis is referred to as a Michaelis–Menten treatment. At low substrate concentrations, the plot shows behavior characteristic of first-order kinetics, but at very high substrate concentrations, the behavior shows zeroth-order kinetics. Explain this phenomenon.
Answers
-
zeroth order in substrate.
-
-
In both cases, the product of pathway A is favored. All of the Z produced in the catalyzed reversible pathway B will eventually be converted to X as X is converted irreversibly to Y by pathway A.
-
14.9 End-of-Chapter Material
Application Problems
-
Atmospheric chemistry in the region below the clouds of Venus appears to be dominated by reactions of sulfur and carbon-containing compounds. Included in representative elementary reactions are the following:
SO2 + CO → SO + CO2 SO + CO → S + CO2 SO + SO2 → S + SO3For each elementary reaction, write an expression for the net rate of reaction in terms of the concentrations of reactants and products.
-
In acid, nitriles hydrolyze to produce a carboxylic acid and ammonium ion. For example, acetonitrile, a substance used to extract fatty acids from fish liver oils, is hydrolyzed to acetic acid via the following reaction:
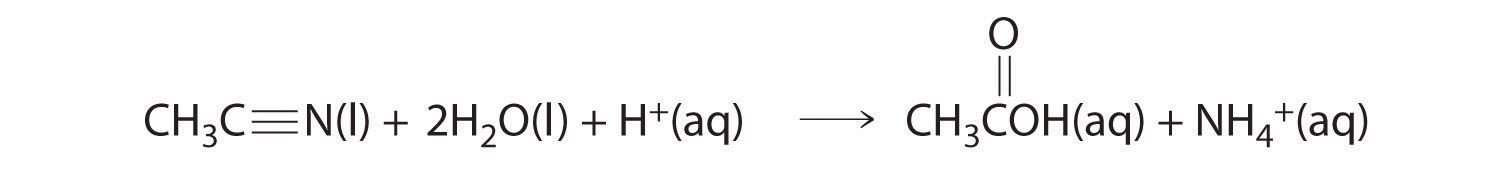
Express the reaction rate in terms of changes in the concentrations of each reactant and each product with time.
-
♦ Ozone production occurs at lower altitudes according to the elementary reaction O + O2 → O3, with an estimated rate of ozone production of 4.86 × 1031 molecules·s−1 worldwide. What is the overall reaction order? If the reaction rate of loss of O3 due to absorption of UV light (Equation 3.36) is 0.89 × 1031 molecules·s−1, and 0.06 × 1031 molecules·s−1 of ozone is transported to other atmospheric regions, is ozone being produced faster than it is being destroyed? Measurements show that ozone concentrations are not increasing rapidly. What conclusion can you draw from these data?
-
♦ The water in a fishery became polluted when toxic waste was dumped into its pond, causing the fish population to substantially decline. The percentage of fish that survived is recorded in the following table.
Day 1 2 3 4 5 % survival 79 55 38 31 19 What is the reaction order of live fish → dead fish? What is the rate constant? If the fish continue to die at this rate, how many fish will be alive after 10 days?
-
Until 200 yr ago, manufactured iron contained charcoal produced from freshly cut wood that was added during the smelting process. As a result of this practice, older samples of iron can be dated accurately using the carbon-14 method. An archaeologist found a cast iron specimen that she believed dated to the period between 480 and 221 BC in Hunan, China. Radiocarbon dating of the sample indicated a 24% reduction in carbon-14 content. Was the archaeologist correct?
-
♦ Because of its short half-life, 32P-labeled compounds must be shipped as quickly as possible so that they can be used as radioactive tags in biological studies. A 50 g sample that contained 0.60% 32P by mass was shipped at 11 a.m. on Monday morning. The package was delivered to a chemist via an overnight delivery service such that it arrived the next day.
- What would be the mass of 32P remaining in the sample if he received the package on Tuesday afternoon but was unable to use it until 9 a.m. on Wednesday?
- What would be the mass of 32P present in the sample if the shipper had not delivered the sample until Friday afternoon and then it sat on a loading dock until 9 a.m. on Monday morning?
- The late shipment was used immediately on Monday morning, but the biological samples were not analyzed until Thursday at 5 p.m. What percentage of the sample still consists of 32P?
-
♦ Tritium (3H) is a radioactive isotope that is commonly used to follow biochemical reactions.
- Using the data in Table 14.6 "Half-Lives and Applications of Some Radioactive Isotopes", calculate the radioactive decay constant (k) for tritium.
- Use the value of k to determine the mass of tritium that is still present in a 5.00 g sample of NaB3H4 that is 17.57 yr old.
-
♦ L-Aspartic acid is an amino acid found in fossil bone. It can convert to a geometrically different form (D-aspartic acid) at 20°C, with a half-life corresponding to the conversion of L → D of 14,000–20,000 yr. If the temperature of an archaeological site is constant, then the extent of the conversion can be used to date fossils. In one such case, archaeologists dated the arrival of humans on the North American continent to be 20,000 yr ago, but the conversion of L-aspartic acid to D-aspartic acid in human fossils indicated that Paleo-Indians were living in California at least 48,000 yr ago. What would be the relative concentrations of the L- and D-forms that produced this result? Carbon-14 has a half-life of approximately 5730 yr. What percentage of the carbon-14 originally present would have been found in the bones?
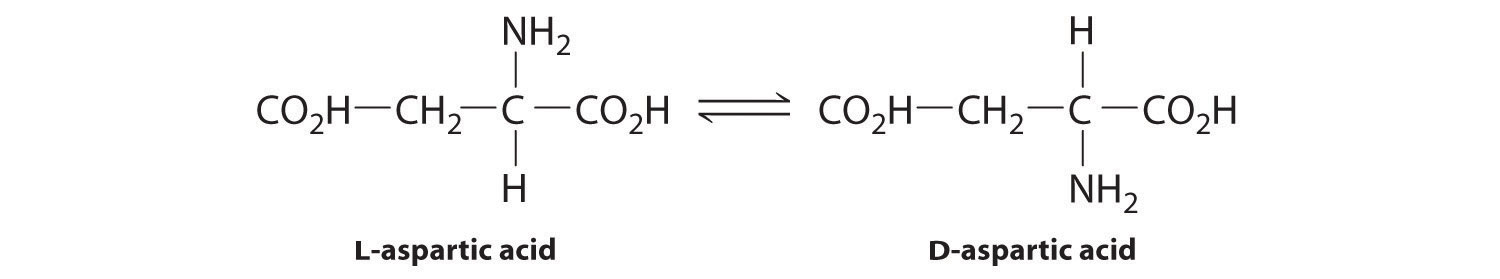
The technique described is frequently used in conjunction with radiocarbon dating. In cases where the results from the two techniques are in gross disagreement, what information can you get by comparing the two results?
-
♦ Peroxides are able to initiate the radical polymerization of alkenes. Polyethylene, for example, is a high-molecular-weight polymer used as a film in packaging, as kitchenware, and as tubing. It is produced by heating ethylene at high pressure in the presence of oxygen or peroxide. It is formed by the following radical process:
RO―CH2―CH2· + CH2=CH2 → RO―CH2―CH2―CH2―CH2·- Label the steps that correspond to initiation and propagation.
- Show all available chain-terminating steps.
- The polymerization of styrene (C6H5CH=CH2) occurs by a similar process to produce polystyrene, which is used as a packaging material. Draw the structure of the polymer that results from five propagation cycles.
-
Lucite and Plexiglas are transparent polymers used as a glass substitute when a plastic material is preferred for safety. The compound used to synthesize Lucite and Plexiglas is methyl methacrylate, which is shown here. During the polymerization reaction, light produces a radical initiator from hydrogen peroxide (H2O2 → 2HO·). Show the mechanism for the polymerization, being sure to include the initiation and propagation steps.
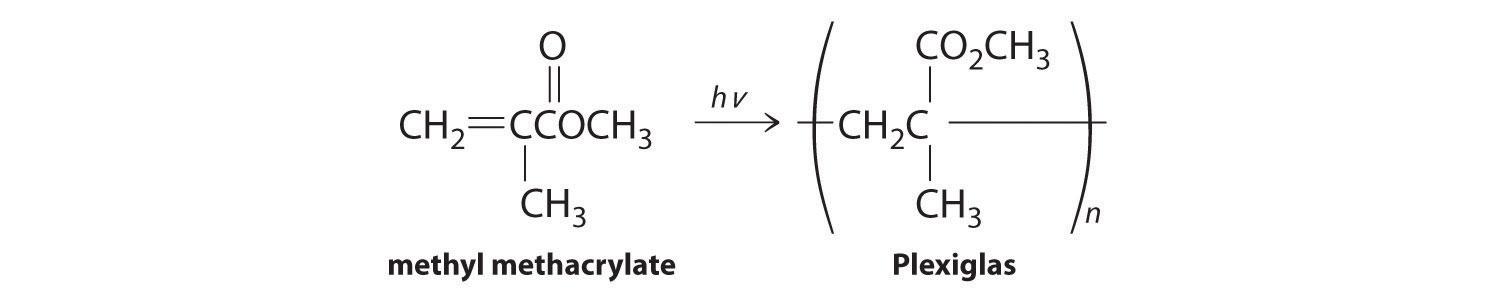
-
♦ At higher altitudes ozone is converted to O2 by the reaction O + O3 → 2O2, with a rate constant at 220 K of 6.8 × 10−16 cm3·molecule−1·s−1.
- What is the overall reaction order?
-
What is Ea for this reaction if A = 8 × 10−12 cm3·molecule−1·s−1?
If Cl is present, the rate constant at 220 K becomes 3.7 × 10−11 cm3·molecule−1 · s−1, with A = 4.7 × 10−11 cm3·molecule−1·s−1.
- Calculate Ea for the depletion of ozone in the presence of Cl.
- Show an energy-level diagram for these two processes, clearly labeling reactants, products, and activation energies.
- If you were an environmental scientist using these data to explain the effects of Cl on ozone concentration, what would be your conclusions?
-
♦ Nitric acid is produced commercially by the catalytic oxidation of ammonia by air over platinum gauze at approximately 900°C. The following reactions occur:
Why is platinum gauze rather than platinum wire used for the initial reaction? The reaction 4NH3(g) + 3O2(g) → 2N2(g) + 6H2O(g) has ΔH° = −316.6 kJ/mol. What would occur if the catalyst were not present? If the gas leaving the catalyst is not free of NH3, the following reaction takes place: 6NO(g) + 4NH3(g) → 5N2(g) + 6H2O(g). If this occurs, what will be the overall reaction?
-
Figure 14.27 "Hydrogenation of Ethylene on a Heterogeneous Catalyst" illustrates the mechanism for the reduction of ethylene on a platinum surface to produce ethane. Industrially important silanes are synthesized using a related mechanism and are used to increase adhesion between layers of glass fiber and between layers of silicone rubber. Predict the products of the following reactions:
-
♦ In catalysis, if a molecule forms strong bonds to the catalyst, then the catalyst may become poisoned. Experiments on various catalysts showed the following results:
- Fe, Ru, and Os form weak bonds with N2; however, O2, alkynes, alkenes, CO, H2, and CO2 interact more strongly.
- CO2 and H2 form weak bonds with a Co or Ni surface.
- Rh, Pd, Ir, and Pt form weak bonds with H2 but do not bond with CO2.
- Cu, Ag, and Au form weak bonds with CO and ethylene.
- Explain why Fe was chosen as a catalyst to convert nitrogen and hydrogen to ammonia. Why is Fe more suitable than Ru or Os?
- Because alkenes generally interact more strongly with metal surfaces than does H2, what catalyst would you choose for hydrogenation of an alkene such as ethylene?
- Although platinum is used in catalytic converters for automobile exhaust, it was not found to be a particularly effective catalyst for the reaction of H2 with a mixture of carbon monoxide and carbon dioxide to produce methane. Why?
- If you were interested in developing a catalyst to reversibly bind ethylene, which of the catalysts listed here would you choose?
-
Nonstoichiometric metal oxides can be effective catalysts for oxidation–reduction reactions. One such catalyst is Ni1−xO, found to be effective for converting CO to CO2 when oxygen is present. Why is it so effective?
-
The chemical reactions in an organism can be controlled by regulating the activity of certain enzymes. Efficient regulation results in an enzyme being active only when it is needed. For example, if a cell needed histidine, the nine enzymes needed to synthesize histidine would all be active. If the cell had adequate histidine, however, those enzymes would be inactive. The following diagram illustrates a situation in which three amino acids (D, F, H) are all synthesized from a common species, A. The numbers above the arrows refer to the enzymes that catalyze each step. Which enzymes would need to be regulated to produce D? F? H?
-
♦ Because phosphorus-32 is incorporated into deoxyribonucleic acid (DNA), it can be used to detect DNA fragments. Consequently, it is used extensively in biological research, including the Human Genome Project, whose goal was to determine the complete sequence of human DNA. If you were to start with a 20 g sample of phosphorus that contained 10% 32P by mass, converted it into DNA via several chemical steps that had an overall yield of 75% and took 25 days, and then incorporated it into bacteria and allowed them to grow for 5 more days, what mass of 32P would be available for analysis at the end of this time?
-
The enzyme urease contains two atoms of nickel and catalyzes the hydrolysis of urea by the following reaction:
H2NC(O)NH2 + H2O → 2NH3 + CO2Urease is one of the most powerful catalysts known. It lowers the activation energy for the hydrolysis of urea from 137 kJ/mol to only 37 kJ/mol. Calculate the ratio of the reaction rate of the catalyzed reaction to the reaction rate of the uncatalyzed reaction at 37°C. Assume that the frequency factor is the same for both reactions.
-
As noted in Section 14.8 "Catalysis", the reaction rate for the hydrogenation of ethylene to give ethane can be increased by heterogeneous catalysts such as Pt or Ni:
The activation energy for the uncatalyzed reaction is large (188 kJ/mol), so the reaction is very slow at room temperature. In the presence of finely divided metallic Ni, the activation energy is only 84 kJ/mol. Calculate the ratio of the reaction rate of the catalyzed reaction to the reaction rate of the uncatalyzed reaction at 75°C.
Problems marked with a ♦ involve multiple concepts.
Answers
-
rate = kf[SO2][CO] − kr[SO][CO2]; rate = kf[SO][CO] − kr[S][CO2]; rate = kf[SO][SO2] − kr[S][SO3]
-
-
The reaction is second order: first order in O and first order in O3. Ozone is being produced faster than it is being destroyed. If ozone concentrations are not increasing, then either some other reaction must be consuming some of the ozone produced in this reaction or the ozone-producing reaction does not operate at this rate continuously.
-
-
Yes; the object is about 2300 yr old.
-
-
- k = 0.05626 yr−1
- 0.487 g of 3H
-
-
-
-
- second order, first order in O and first order in O3;
- 17 kJ/mol;
- 0.44 kJ/mol;
-
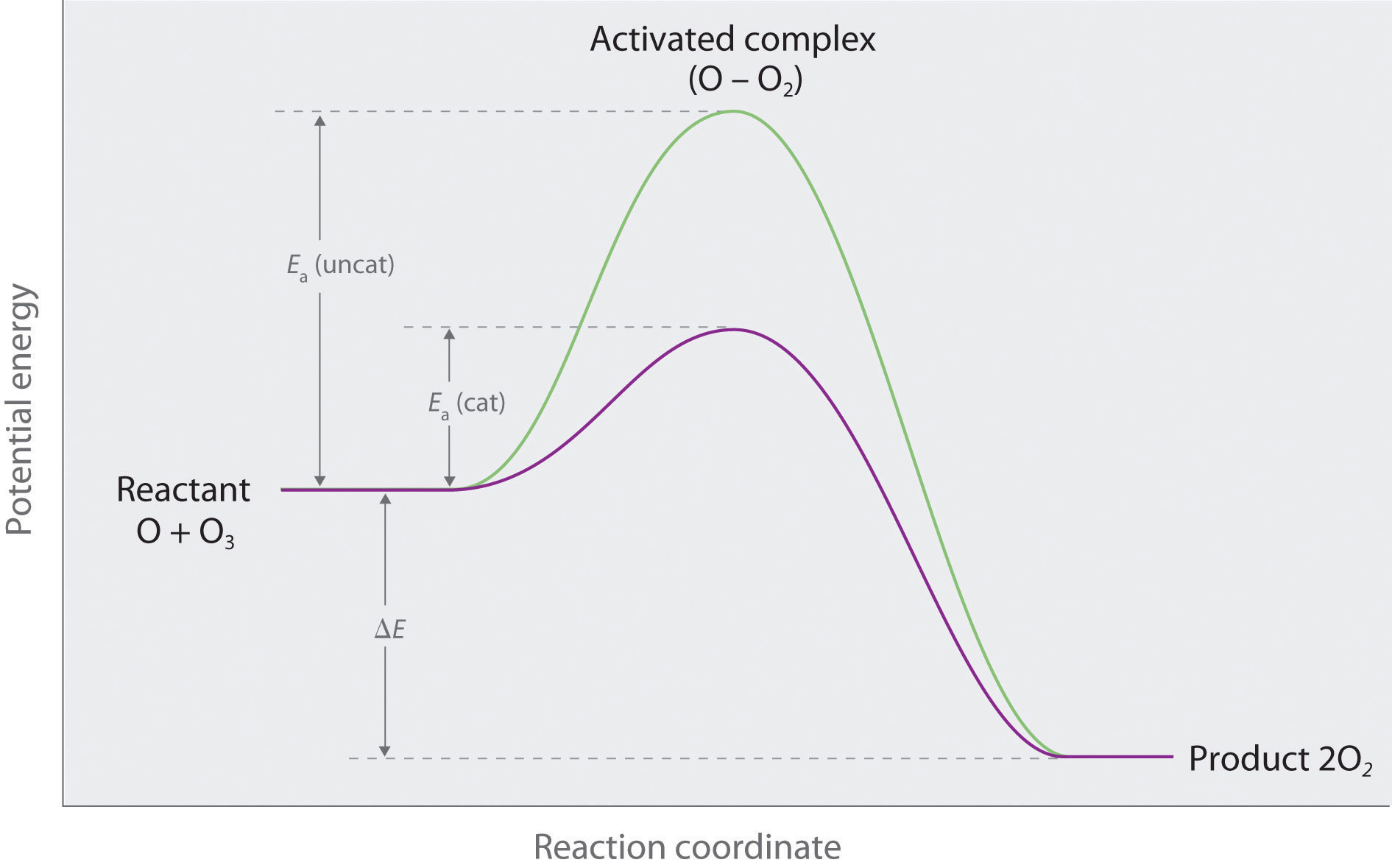
- Cl is a potent catalyst for ozone destruction because there is a large decrease in Ea when Cl is present.
-
-
-
-
Ni1−xO is a nonstoichiometric oxide that contains a fraction of Ni(I) sites. These can react with oxygen to form a Ni(III)-oxide site, which is reduced by CO to give Ni(I) and CO2.
-
-
0.35 g of 32P
-
-
4.1 × 1015




