This is “Review Exercises and Sample Exam”, section 8.6 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
8.6 Review Exercises and Sample Exam
Review Exercises
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Distance, Midpoint, and the Parabola
Calculate the distance and midpoint between the given two points.
Determine the area of a circle whose diameter is defined by the given two points.
Rewrite in standard form and give the vertex.
Rewrite in standard form and graph. Be sure to find the vertex and all intercepts.
-
-
-
-
-
Center with radius
-
Center with radius
-
Center with radius
-
Center with radius
-
Circle whose diameter is defined by and
-
Circle whose diameter is defined by and
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Circles
Determine the center and radius given the equation of a circle in standard form.
Determine standard form for the equation of the circle:
Find the x- and y-intercepts.
Graph.
Rewrite in standard form and graph.
-
-
-
-
-
Center with and
-
Center with and
-
Center with and
-
Center with and
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Ellipses
Given the equation of an ellipse in standard form, determine its center, orientation, major radius, and minor radius.
Determine the standard form for the equation of the ellipse given the following information.
Find the x- and y-intercepts.
Graph.
Rewrite in standard form and graph.
-
-
-
-
-
Center , , , opens up and down.
-
Center , , , opens left and right.
-
Center , , , opens left and right.
-
Center , , , opens up and down.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
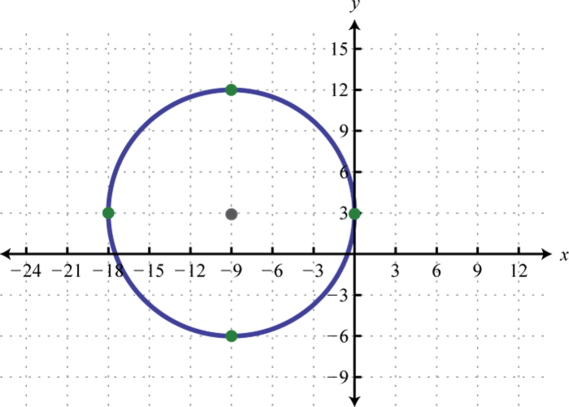
-
-

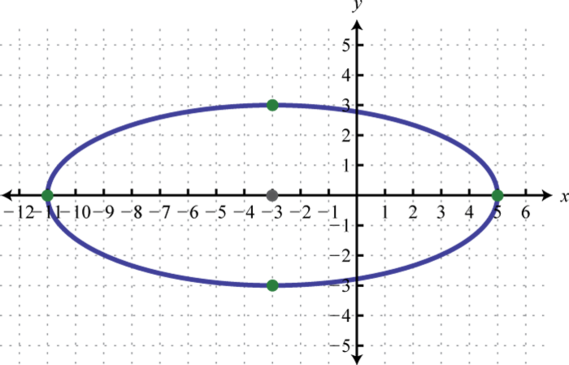
-

-
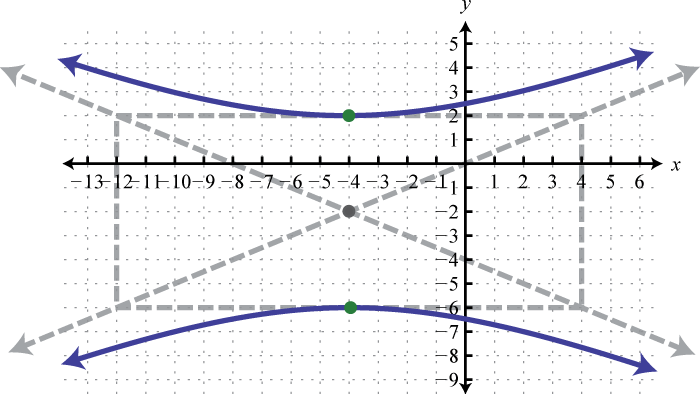
-
Hyperbolas
Given the equation of a hyperbola in standard form, determine its center, which way the graph opens, and the vertices.
Determine the standard form for the equation of the hyperbola.
Find the x- and y-intercepts.
Graph.
Rewrite in standard form and graph.
Identify the conic sections and rewrite in standard form.
Given the graph, write the equation in general form.
Solving Nonlinear Systems
Solve.
Answers
-
Distance: 5 units; midpoint:
-
-
Distance: units; midpoint:
-
-
Distance: units; midpoint:
-
-
square units
-
-
square units
-
-
; vertex:
-
-
; vertex:
-
-
; vertex:
-
-
; vertex:
-
-
;
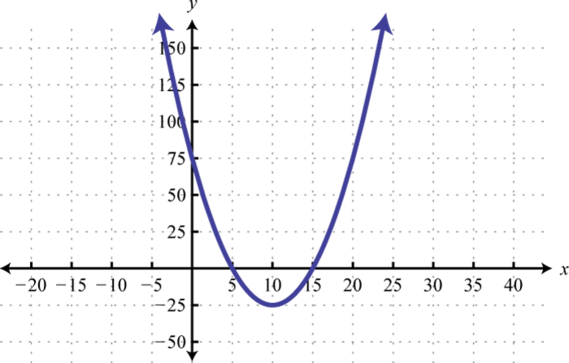
-
-
;
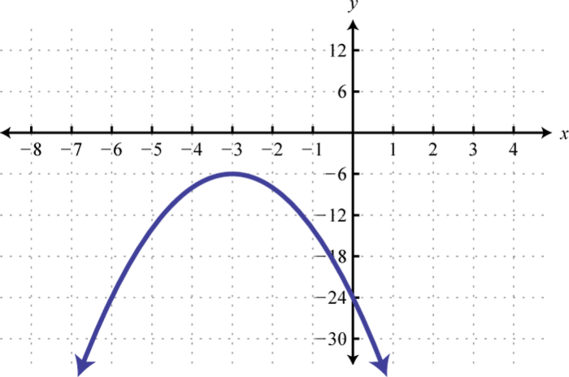
-
-
;

-
-
;
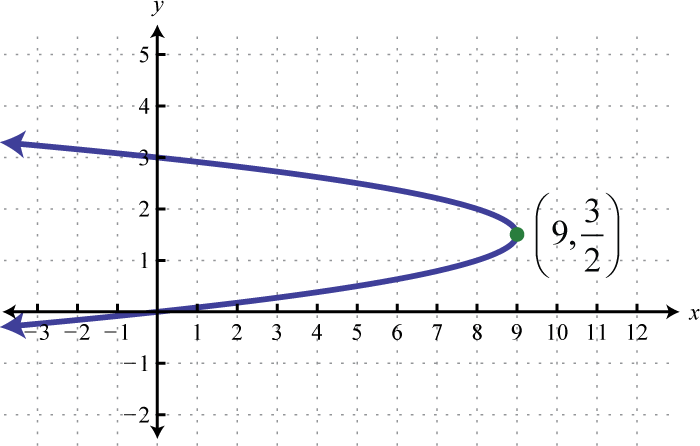
-
-
;
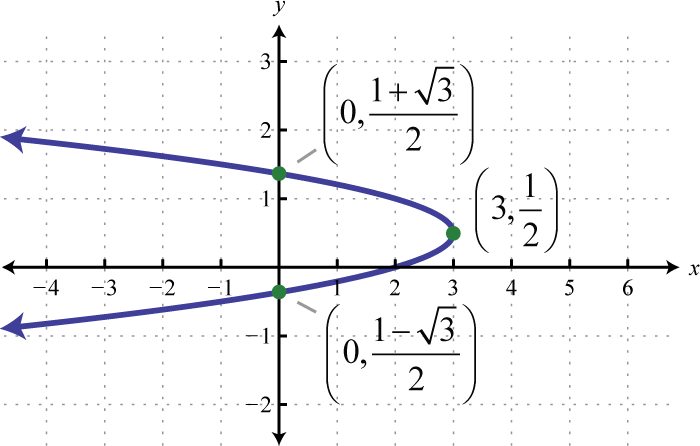
-
-
Center: ; radius:
-
-
Center: ; radius:
-
-
-
-
-
-
-
-
x-intercepts: none; y-intercepts:
-
-
x-intercepts: ; y-intercepts:
-
-
x-intercepts: none; y-intercepts: ,
-
-
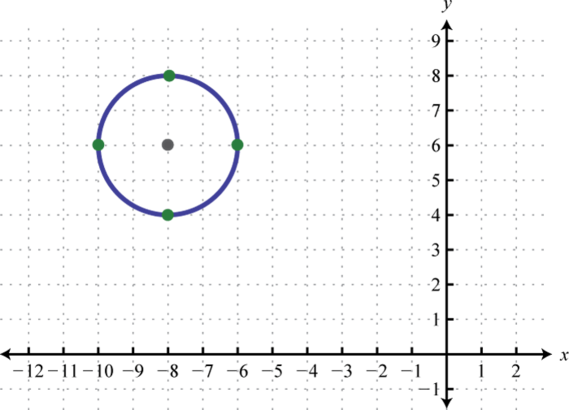
-
-
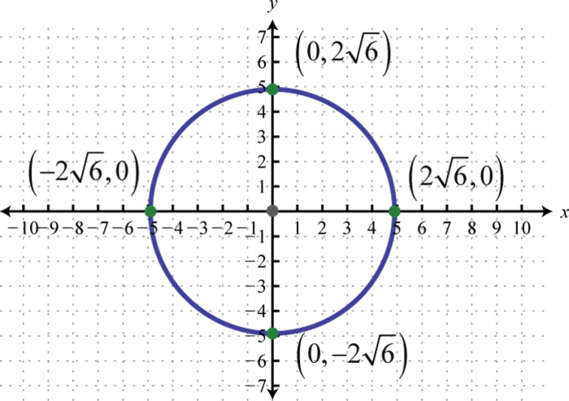
-
-
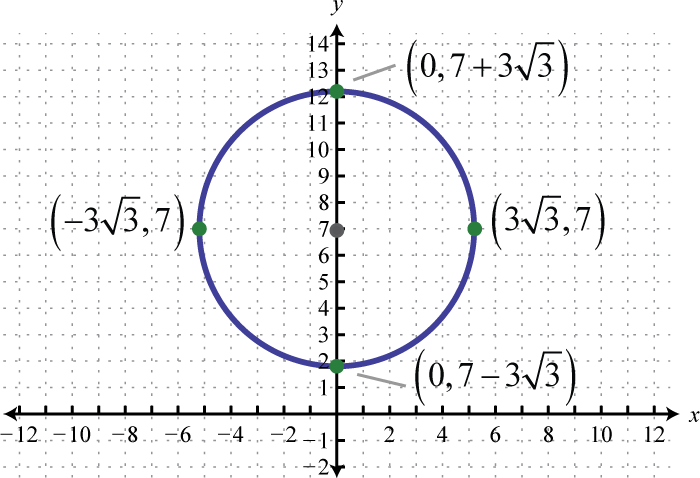
-
-
;

-
-
;
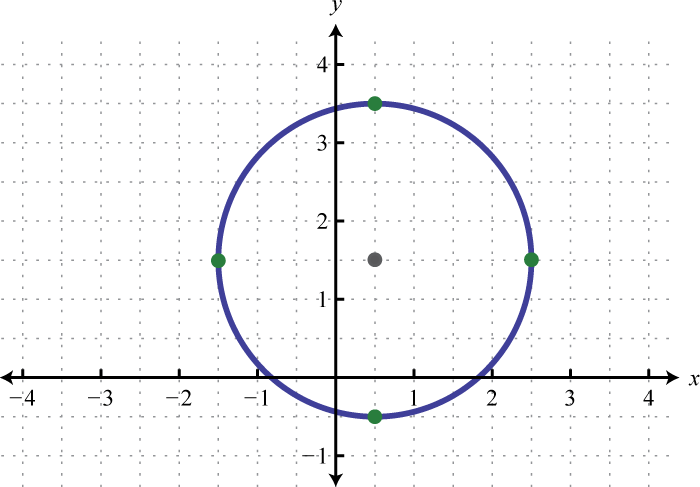
-
-
;

-
-
Center: ; orientation: horizontal; major radius: 4 units; minor radius: 2 units
-
-
Center: ; orientation: vertical; major radius: units; minor radius: 1 unit
-
-
-
-
-
-
x-intercepts: , ; y-intercepts:
-
-
x-intercepts: ; y-intercepts:
-
-
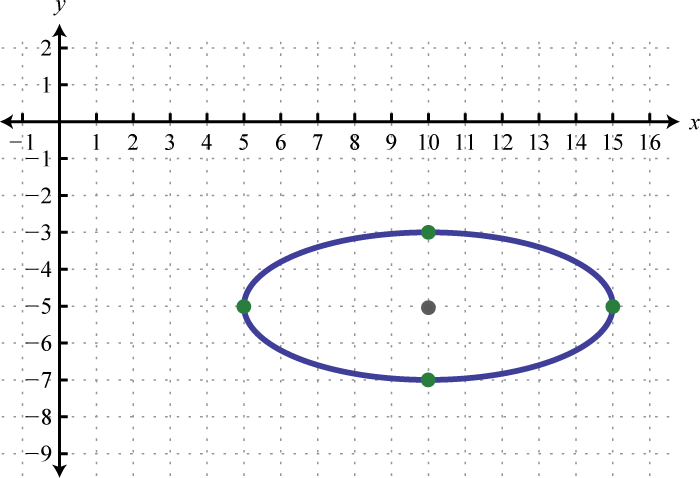
-
-
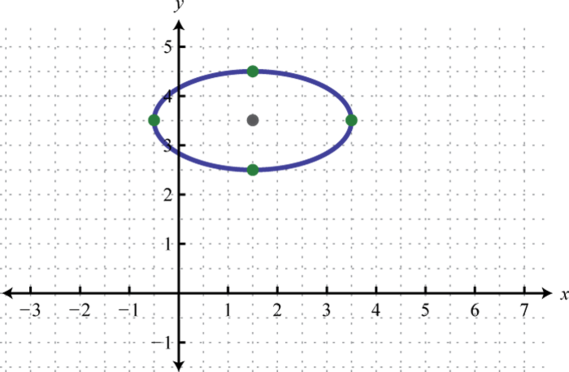
-
-
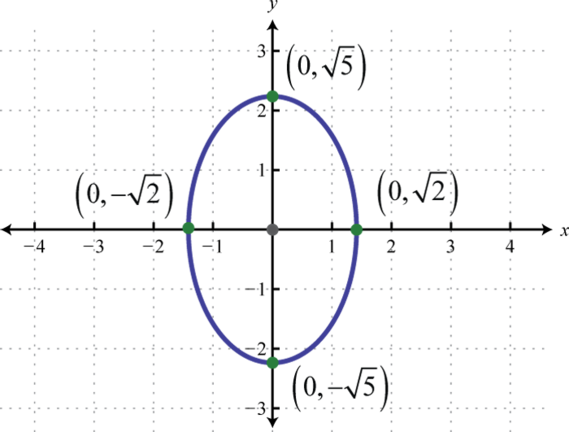
-
-
;
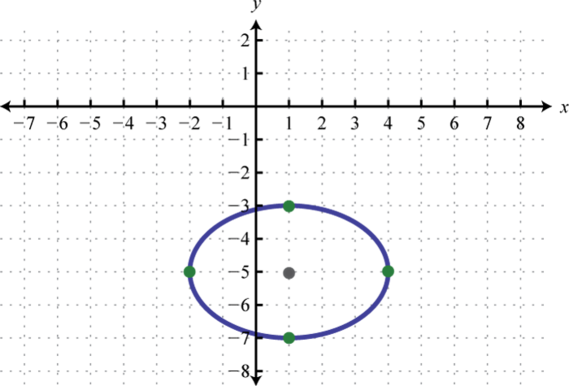
-
-
;

-
-
;

-
-
Center: ; opens left and right; vertices: ,
-
-
Center: ; opens upward and downward; vertices: ,
-
-
-
-
-
-
x-intercepts: ; y-intercepts: none
-
-
x-intercepts: ; y-intercepts: ,
-
-
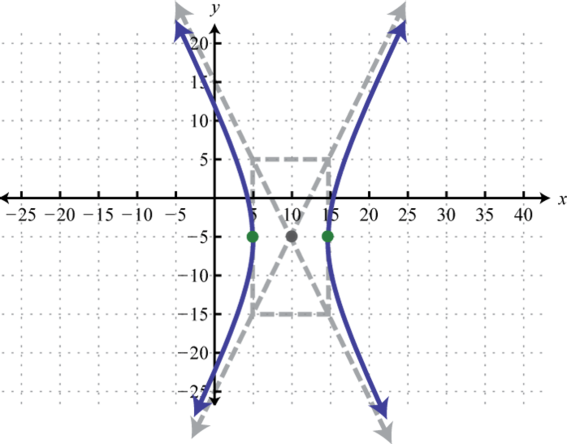
-
-
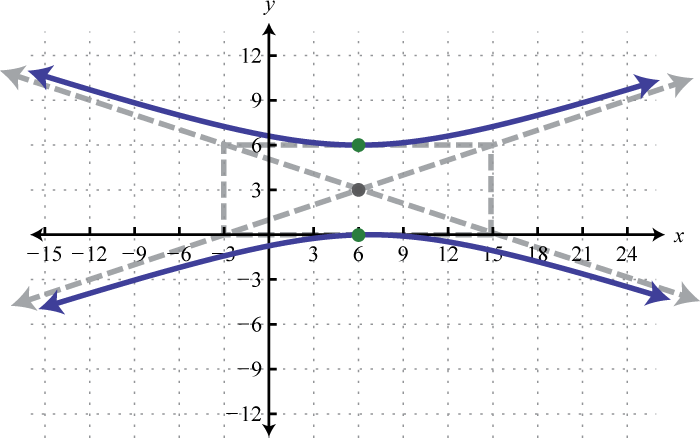
-
-
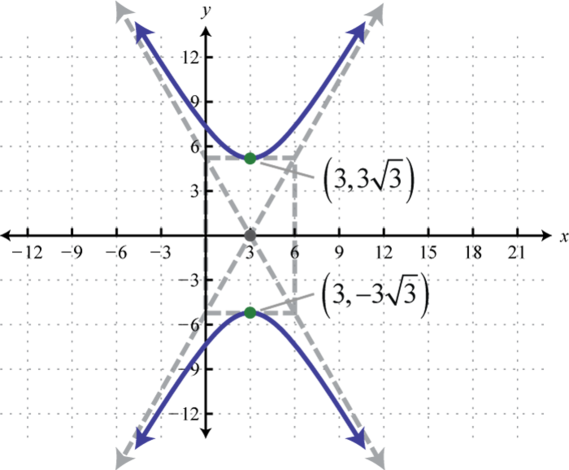
-
-
;
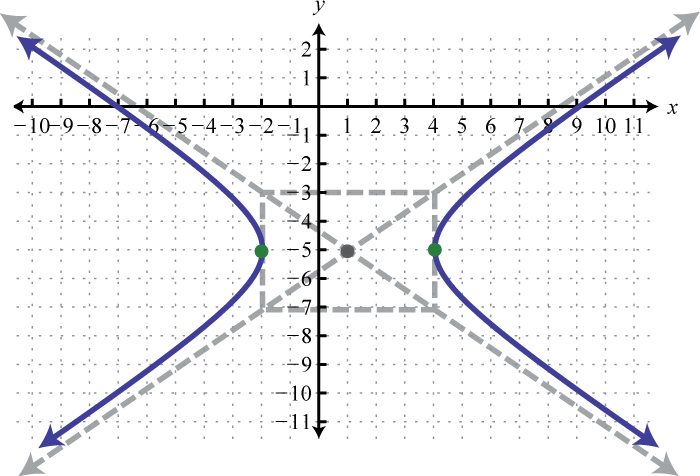
-
-
;
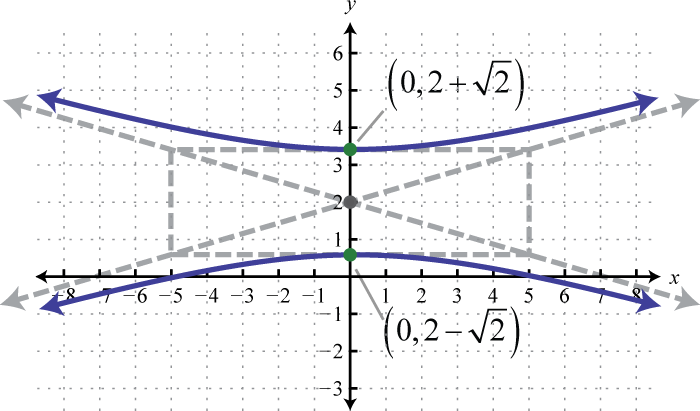
-
-
;

-
-
Circle;
-
-
Hyperbola;
-
-
Ellipse;
-
-
Hyperbola;
-
-
Hyperbola;
-
-
-
-
-
-
-
-
-
-
,
-
-
,
-
-
,
-
-
, , ,
-
-
, , ,
-
-
-
-
-
Sample Exam
-
Given two points and :
- Calculate the distance between them.
- Find the midpoint between them.
-
Determine the area of a circle whose diameter is defined by the points and
-
-
-
-
Find the equation of a circle in standard form with center and radius units.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Find the equation of an ellipse in standard form with vertices and and a minor radius 2 units in length.
-
Find the equation of a hyperbola in standard form opening left and right with vertices and a conjugate axis that measures 10 units.
-
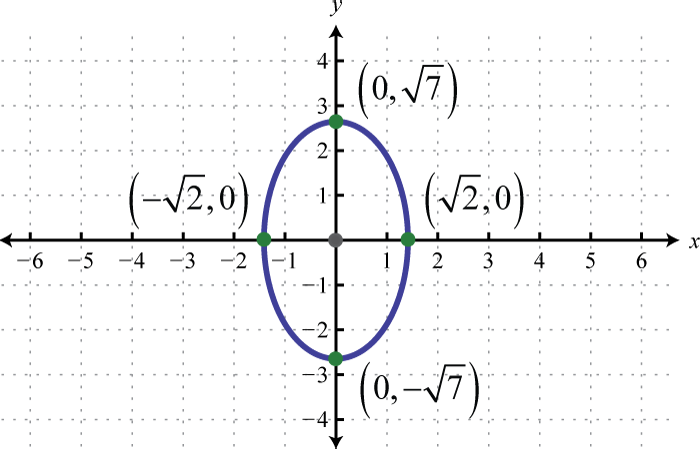
Given the graph of the ellipse, determine its equation in general form.
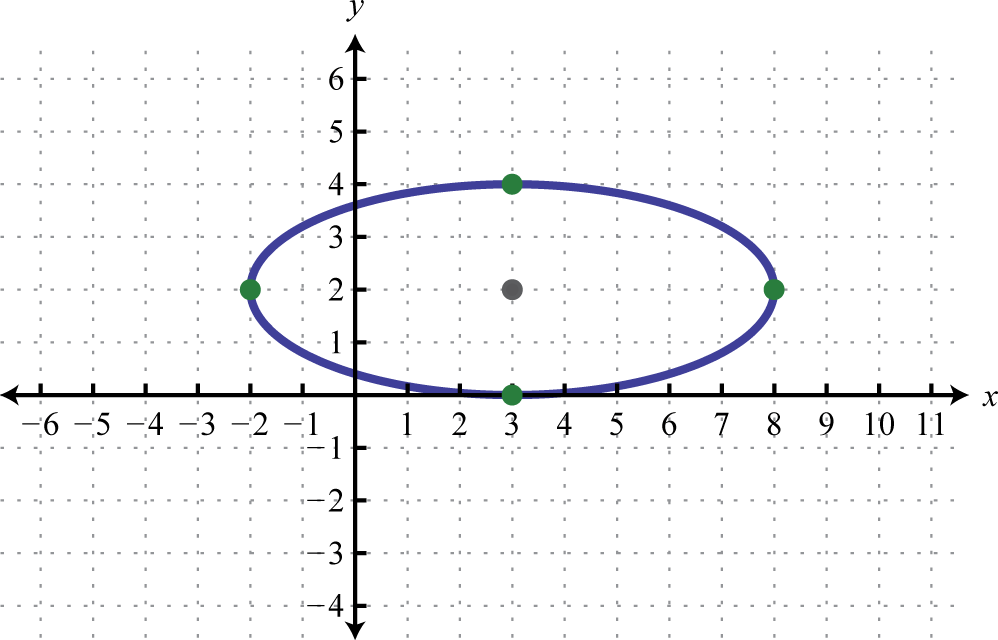
-
A rectangular deck has an area of 80 square feet and a perimeter that measures 36 feet. Find the dimensions of the deck.
-
The diagonal of a rectangle measures centimeters and the perimeter measures 20 centimeters. Find the dimensions of the rectangle.
Rewrite in standard form and graph. Find the vertex and all intercepts if any.
Sketch the graph of the conic section given its equation in standard form.
Rewrite in standard form and graph.
Find the x- and y-intercepts.
Solve.
Answers
-
- units;
-
-
;
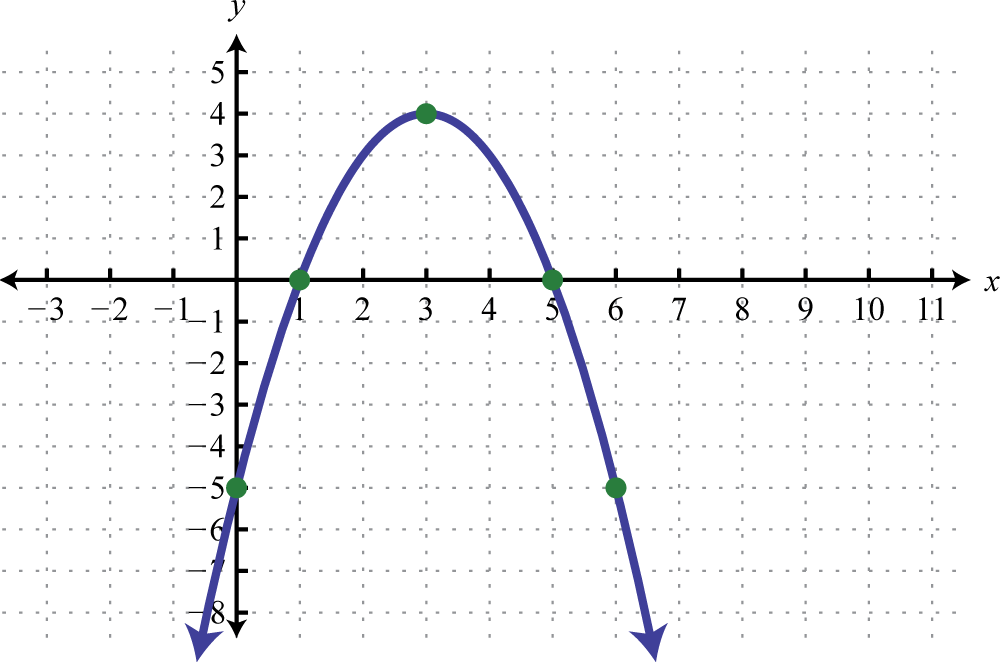
-
-
;
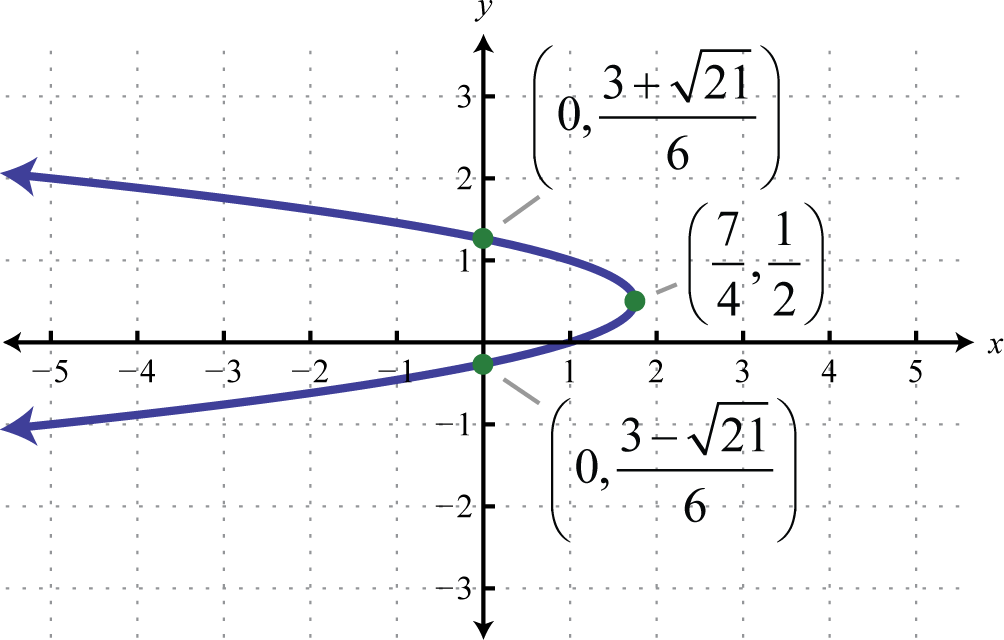
-
-

-
-
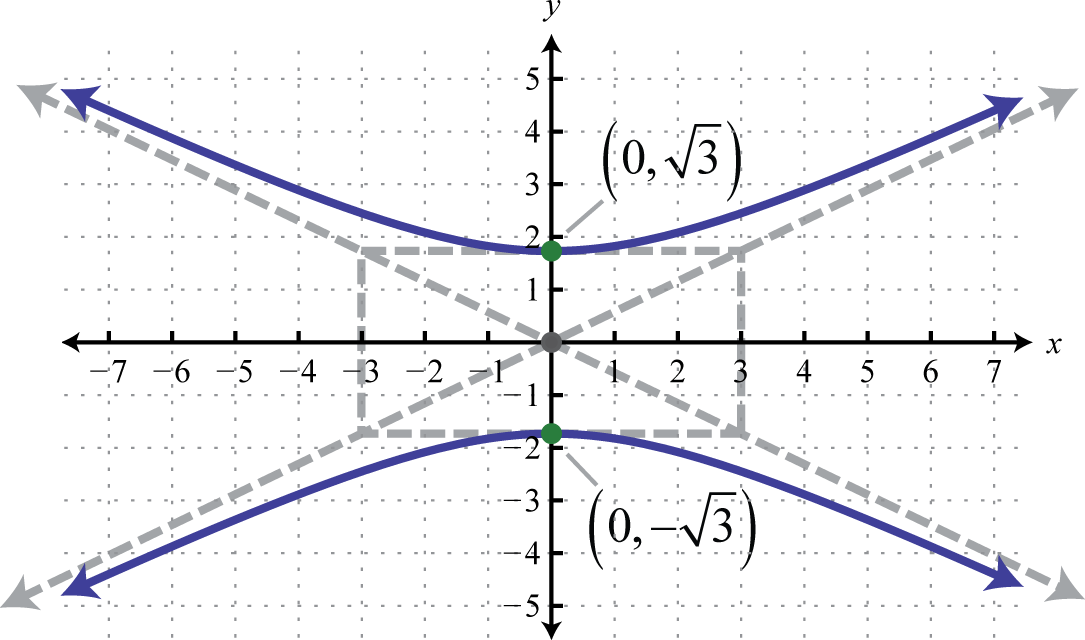
-
-
;
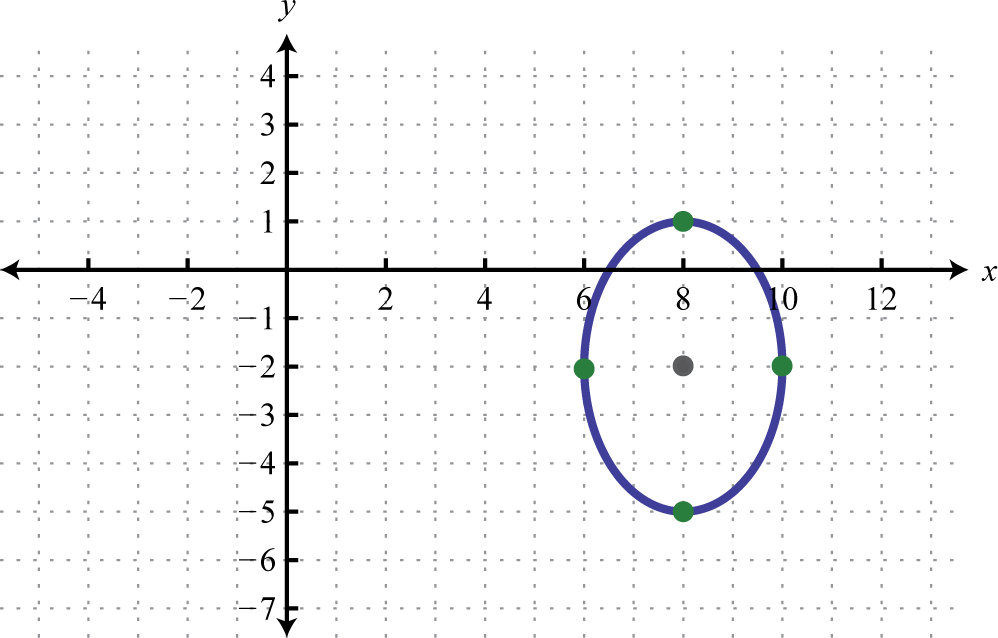
-
-
;
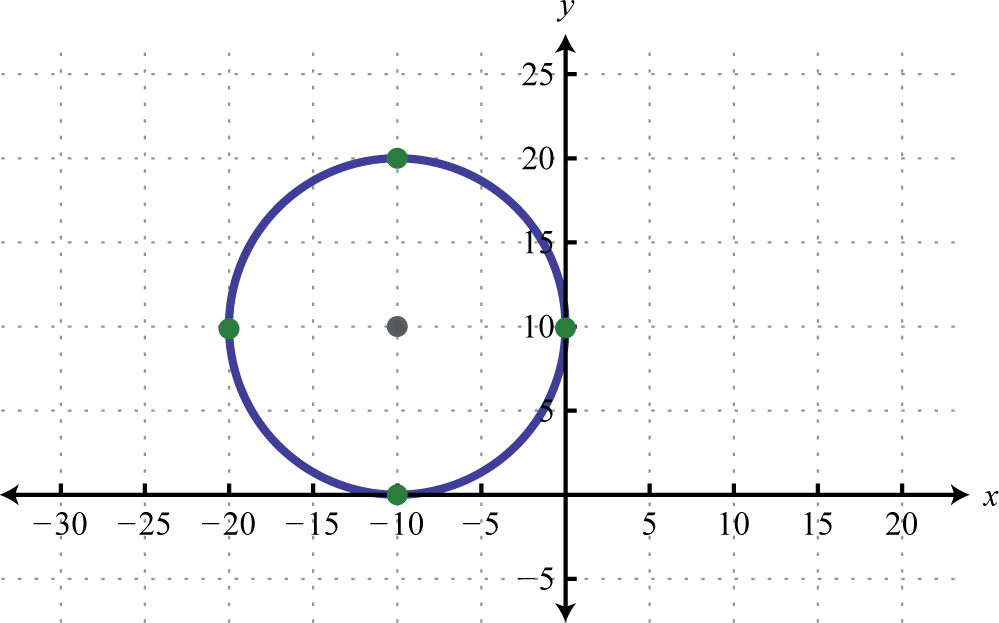
-
-
x-intercept: ; y-intercepts:
-
-
,
-
-
Ø
-
-
-
-
-
-
6 centimeters by 4 centimeters




