This is “Solutions”, chapter 13 from the book Principles of General Chemistry (v. 1.0M). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 13 Solutions
We explored the general properties of gases, liquids, and solids in Chapter 10 "Gases", Chapter 11 "Liquids", and Chapter 12 "Solids", respectively. Most of the discussion focused on pure substances containing a single kind of atom, molecule, or cation–anion pair. The substances we encounter in our daily lives, however, are usually mixtures rather than pure substances. Some are heterogeneous mixtures, which consist of at least two phases that are not uniformly dispersed on a microscopic scale; others are homogeneous mixtures, consisting of a single phase in which the components are uniformly distributed. (For more information about homogeneous mixtures, see Chapter 1 "Introduction to Chemistry", Section 1.3 "A Description of Matter".) Homogeneous mixtures are also called solutionsA homogeneous mixture of two or more substances in which the substances present in lesser amounts (the solutes) are dispersed uniformly throughout the substance present in greater amount (the solvent).; they include the air we breathe, the gas we use to cook and heat our homes, the water we drink, the gasoline or diesel fuel that powers engines, and the gold and silver jewelry we wear.
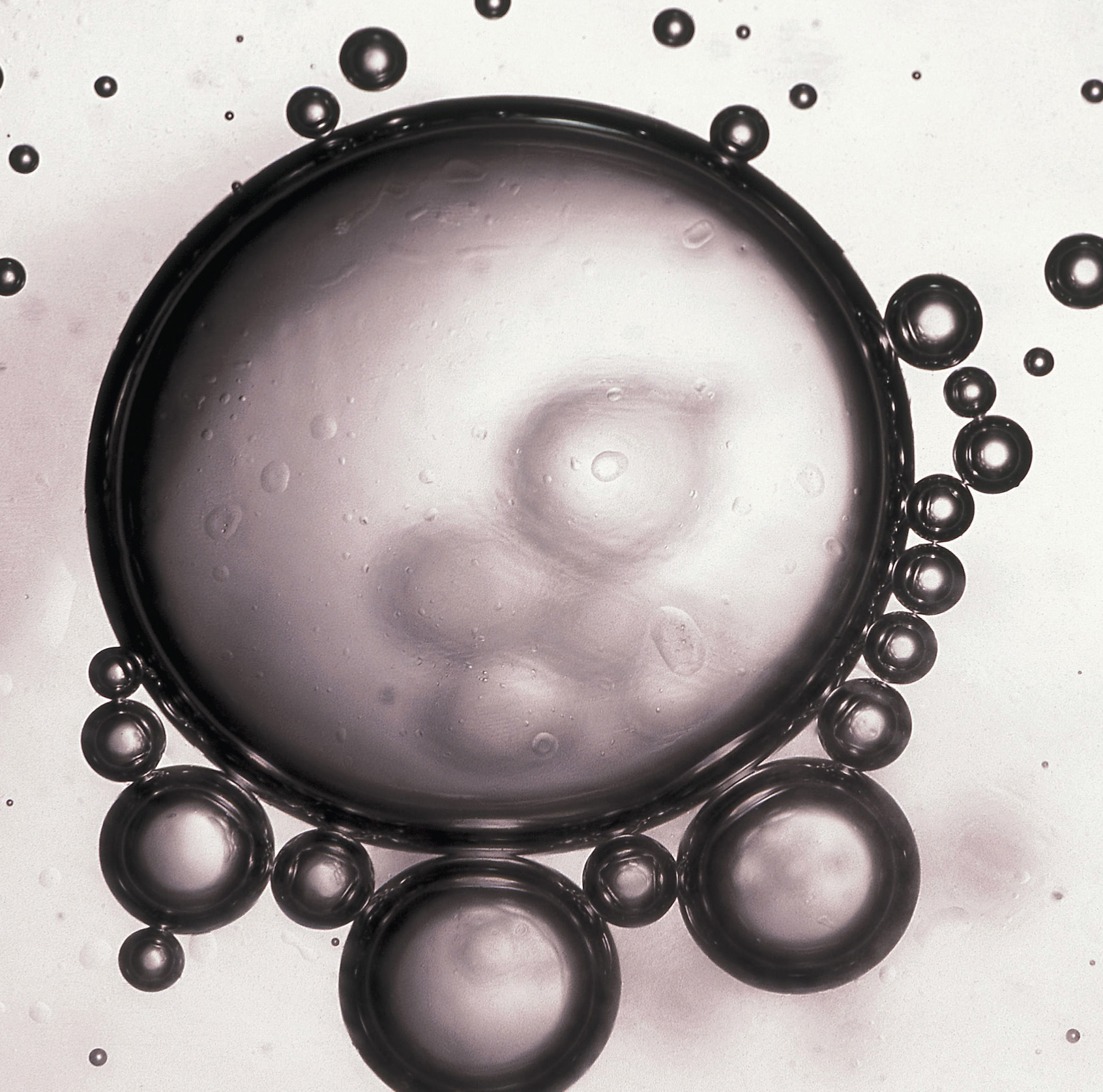
Beads of oil in water. When a nonpolar liquid such as oil is dispersed in a polar solvent such as water, it does not dissolve, but forms spherical beads. Oil is insoluble in water because the intermolecular interactions within the solute (oil) and the solvent (water) are stronger than the intermolecular interactions between the solute and the solvent.
Many of the concepts that we will use in our discussion of solutions were introduced in earlier chapters. In Chapter 4 "Reactions in Aqueous Solution", for example, we described reactions that occur in aqueous solution and how to use molarity to describe concentrations. In Chapter 4 "Reactions in Aqueous Solution", Chapter 7 "The Periodic Table and Periodic Trends", and Chapter 11 "Liquids", we introduced the principles that govern ion–ion and molecule–molecule interactions in pure substances; similar interactions also occur in solutions. Now we use the principles developed in those chapters to understand the factors that determine how much of one substance can dissolve in another, and how the properties of a solution differ from those of its components.
The properties of mixtures of gases were described in Chapter 10 "Gases", and the properties of certain types of solid solutions, such as alloys and doped semiconductors, were discussed in Chapter 12 "Solids". This chapter focuses on liquid solutions, aqueous or otherwise. By the end of this chapter, your understanding of solutions will enable you to explain why the radiator in your car must contain ethylene glycol to avoid damage to the engine on cold winter nights, why salt is spread on icy roads in the winter (and why it isn’t effective when the temperature is too low), why certain vitamins accumulate in your body at toxic levels while others are rapidly excreted, and how salt can be removed from seawater to provide drinking water.
13.1 Factors Affecting Solution Formation
Learning Objective
- To understand how enthalpy and entropy changes affect solution formation.
In all solutions, whether gaseous, liquid, or solid, the substance present in the greatest amount is the solvent, and the substance or substances present in lesser amounts are the solute(s). The solute does not have to be in the same physical state as the solvent, but the physical state of the solvent usually determines the state of the solution. As long as the solute and solvent combine to give a homogeneous solution, the solute is said to be soluble in the solvent. Table 13.1 "Types of Solutions" lists some common examples of gaseous, liquid, and solid solutions and identifies the physical states of the solute and solvent in each.
Table 13.1 Types of Solutions
| Solution | Solute | Solvent | Examples |
|---|---|---|---|
| gas | gas | gas | air, natural gas |
| liquid | gas | liquid | seltzer water (CO2 gas in water) |
| liquid | liquid | liquid | alcoholic beverage (ethanol in water), gasoline |
| liquid | solid | liquid | tea, salt water |
| solid | gas | solid | H2 in Pd (used for H2 storage) |
| solid | solid | liquid | mercury in silver or gold (amalgam often used in dentistry) |
Forming a Solution
The formation of a solution from a solute and a solvent is a physical process, not a chemical one. That is, both solute and solvent can be recovered in chemically unchanged forms using appropriate separation methods. For example, solid zinc nitrate dissolves in water to form an aqueous solution of zinc nitrate:
Equation 13.1
Because Zn(NO3)2 can be recovered easily by evaporating the water, this is a physical process. In contrast, metallic zinc appears to dissolve in aqueous hydrochloric acid. In fact, the two substances undergo a chemical reaction to form an aqueous solution of zinc chloride with evolution of hydrogen gas:
Equation 13.2
Zn(s) + 2H+(aq) + 2Cl−(aq) → Zn2+(aq) + 2Cl−(aq) + H2(g)Note the Pattern
Dissolution of a solute in a solvent to form a solution does not involve a chemical transformation.
When the solution evaporates, we do not recover metallic zinc, so we cannot say that metallic zinc is soluble in aqueous hydrochloric acid because it is chemically transformed when it dissolves. The dissolution of a solute in a solvent to form a solution does not involve a chemical transformation.
Substances that form a single homogeneous phase in all proportions are said to be completely miscibleCapable of forming a single homogeneous phase, regardless of the proportions with which the substances are mixed. in one another. Ethanol and water are miscible, just as mixtures of gases are miscible. If two substances are essentially insoluble in each other, such as oil and water, they are immiscible. Examples of gaseous solutions that we have already discussed include Earth’s atmosphere (see Chapter 3 "Chemical Reactions") and natural gas (see Chapter 10 "Gases").
The Role of Enthalpy in Solution Formation
As we saw in Chapter 10 "Gases"–Chapter 12 "Solids", energy is required to overcome the intermolecular interactions in a solute. This energy can be supplied only by the new interactions that occur in the solution, when each solute particle is surrounded by particles of the solvent in a process called solvationThe process of surrounding each solute particle with particles of solvent., or hydrationThe process of surrounding solute particles with water molecules. when the solvent is water. Thus all of the solute–solute interactions and many of the solvent–solvent interactions must be disrupted for a solution to form. In this section, we describe the role of enthalpy in this process.
Because enthalpy is a state function, we can use the same type of thermochemical cycle described in Chapter 5 "Energy Changes in Chemical Reactions" to analyze the energetics of solution formation. (For more information about state functions, see Chapter 5 "Energy Changes in Chemical Reactions", Section 5.2 "Enthalpy".) The process occurs in three discrete steps, indicated by ΔH1, ΔH2, and ΔH3 in Figure 13.1 "Enthalpy Changes That Accompany the Formation of a Solution". The overall enthalpy change in the formation of the solution (ΔHsoln) is the sum of the enthalpy changes in the three steps:
Equation 13.3
ΔHsoln = ΔH1 + ΔH2 + ΔH3When a solvent is added to a solution, steps 1 and 2 are both endothermic because energy is required to overcome the intermolecular interactions in the solvent (ΔH1) and the solute (ΔH2). Because ΔH is positive for both steps 1 and 2, the solute–solvent interactions (ΔH3) must be stronger than the solute–solute and solvent–solvent interactions they replace in order for the dissolution process to be exothermic (ΔHsoln < 0). When the solute is an ionic solid, ΔH2 corresponds to the lattice energy that must be overcome to form a solution. As you learned in Chapter 12 "Solids", the higher the charge of the ions in an ionic solid, the higher the lattice energy. Consequently, solids that have very high lattice energies, such as MgO (−3791 kJ/mol), are generally insoluble in all solvents.
Figure 13.1 Enthalpy Changes That Accompany the Formation of a Solution
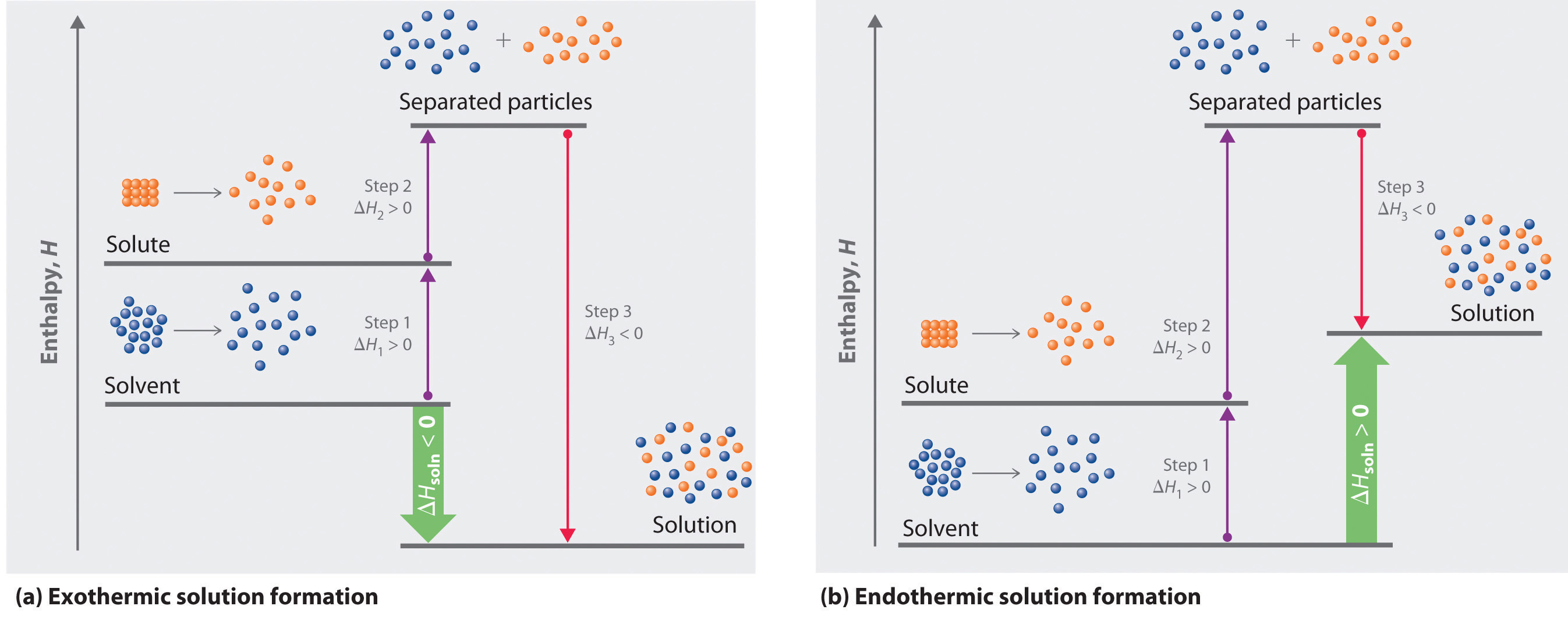
Solvation can be an exothermic or endothermic process depending on the nature of the solute and solvent. In both cases, step 1, separation of the solvent particles, is energetically uphill (ΔH1 > 0), as is step 2, separation of the solute particles (ΔH2 > 0). In contrast, energy is released in step 3 (ΔH3 < 0) because of interactions between the solute and solvent. (a) When ΔH3 is larger in magnitude than the sum of ΔH1 and ΔH2, the overall process is exothermic (ΔHsoln < 0), as shown in the thermochemical cycle. (b) When ΔH3 is smaller in magnitude than the sum of ΔH1 and ΔH2, the overall process is endothermic (ΔHsoln > 0).
As you will see in Chapter 18 "Chemical Thermodynamics", a positive value for ΔHsoln does not mean that a solution will not form. Whether a given process, including formation of a solution, occurs spontaneously depends on whether the total energy of the system is lowered as a result. Enthalpy is only one of the contributing factors. A high ΔHsoln is usually an indication that the substance is not very soluble. Instant cold packs used to treat athletic injuries, for example, take advantage of the large positive ΔHsoln of ammonium nitrate during dissolution (+25.7 kJ/mol), which produces temperatures less than 0°C (Figure 13.2 "Commercial Cold Packs for Treating Injuries").
Figure 13.2 Commercial Cold Packs for Treating Injuries

These packs contain solid NH4NO3 and water in separate compartments. When the seal between the compartments is broken, the NH4NO3 dissolves in the water. Because ΔHsoln for NH4NO3 is much greater than zero, heat is absorbed by the cold pack during the dissolution process, producing local temperatures less than 0°C.
Entropy and Solution Formation
The enthalpy change that accompanies a process is important because processes that release substantial amounts of energy tend to occur spontaneously. A second property of any system, its entropy, is also important in helping us determine whether a given process occurs spontaneously. We will discuss entropy in more detail in Chapter 18 "Chemical Thermodynamics", but for now we can state that entropy(S)The degree of disorder in a thermodynamic system. The greater the number of possible microstates for a system, the higher the entropy. is a thermodynamic property of all substances that is proportional to their degree of disorder. A perfect crystal at 0 K, whose atoms are regularly arranged in a perfect lattice and are motionless, is arbitrarily assigned an entropy of zero. In contrast, gases have large positive entropies because their molecules are highly disordered and in constant motion at high speeds.
The formation of a solution disperses molecules, atoms, or ions of one kind throughout a second substance, which generally increases the disorder and results in an increase in the entropy of the system. Thus entropic factors almost always favor formation of a solution. In contrast, a change in enthalpy may or may not favor solution formation. The London dispersion forces that hold cyclohexane and n-hexane together in pure liquids, for example, are similar in nature and strength. Consequently, ΔHsoln should be approximately zero, as is observed experimentally. Mixing equal amounts of the two liquids, however, produces a solution in which the n-hexane and cyclohexane molecules are uniformly distributed over approximately twice the initial volume. In this case, the driving force for solution formation is not a negative ΔHsoln but rather the increase in entropy due to the increased disorder in the mixture. All spontaneous processes with ΔH ≥ 0 are characterized by an increase in entropy. In other cases, such as mixing oil with water, salt with gasoline, or sugar with hexane, the enthalpy of solution is large and positive, and the increase in entropy resulting from solution formation is not enough to overcome it. Thus in these cases a solution does not form.
Note the Pattern
All spontaneous processes with ΔH ≥ 0 are characterized by an increase in entropy.
Table 13.2 "Relative Changes in Enthalpies for Different Solute–Solvent Combinations*" summarizes how enthalpic factors affect solution formation for four general cases. The column on the far right uses the relative magnitudes of the enthalpic contributions to predict whether a solution will form from each of the four. Keep in mind that in each case entropy favors solution formation. In two of the cases the enthalpy of solution is expected to be relatively small and can be either positive or negative. Thus the entropic contribution dominates, and we expect a solution to form readily. In the other two cases the enthalpy of solution is expected to be large and positive. The entropic contribution, though favorable, is usually too small to overcome the unfavorable enthalpy term. Hence we expect that a solution will not form readily.
Table 13.2 Relative Changes in Enthalpies for Different Solute–Solvent Combinations*
| ΔH1 (separation of solvent molecules) | ΔH2 (separation of solute particles) | ΔH3 (solute–solvent interactions) | ΔHsoln (ΔH1 + ΔH2 +ΔH3) | Result of Mixing Solute and Solvent† |
|---|---|---|---|---|
| large; positive | large; positive | large; negative | small; positive or negative | solution will usually form |
| small; positive | large; positive | small; negative | large; positive | solution will not form |
| large; positive | small; positive | small; negative | large; positive | solution will not form |
| small; positive | small; positive | small; negative | small; positive or negative | solution will usually form |
| *ΔH1, ΔH2, and ΔH3 refer to the processes indicated in the thermochemical cycle shown in Figure 13.1 "Enthalpy Changes That Accompany the Formation of a Solution". | ||||
| †In all four cases, entropy increases. | ||||
In contrast to liquid solutions, the intermolecular interactions in gases are weak (they are considered to be nonexistent in ideal gases). Hence mixing gases is usually a thermally neutral process (ΔHsoln ≈ 0), and the entropic factor due to the increase in disorder is dominant (Figure 13.3 "Formation of a Solution of Two Gases"). Consequently, all gases dissolve readily in one another in all proportions to form solutions. We will return to a discussion of enthalpy and entropy in Chapter 18 "Chemical Thermodynamics", where we treat their relationship quantitatively.
Figure 13.3 Formation of a Solution of Two Gases
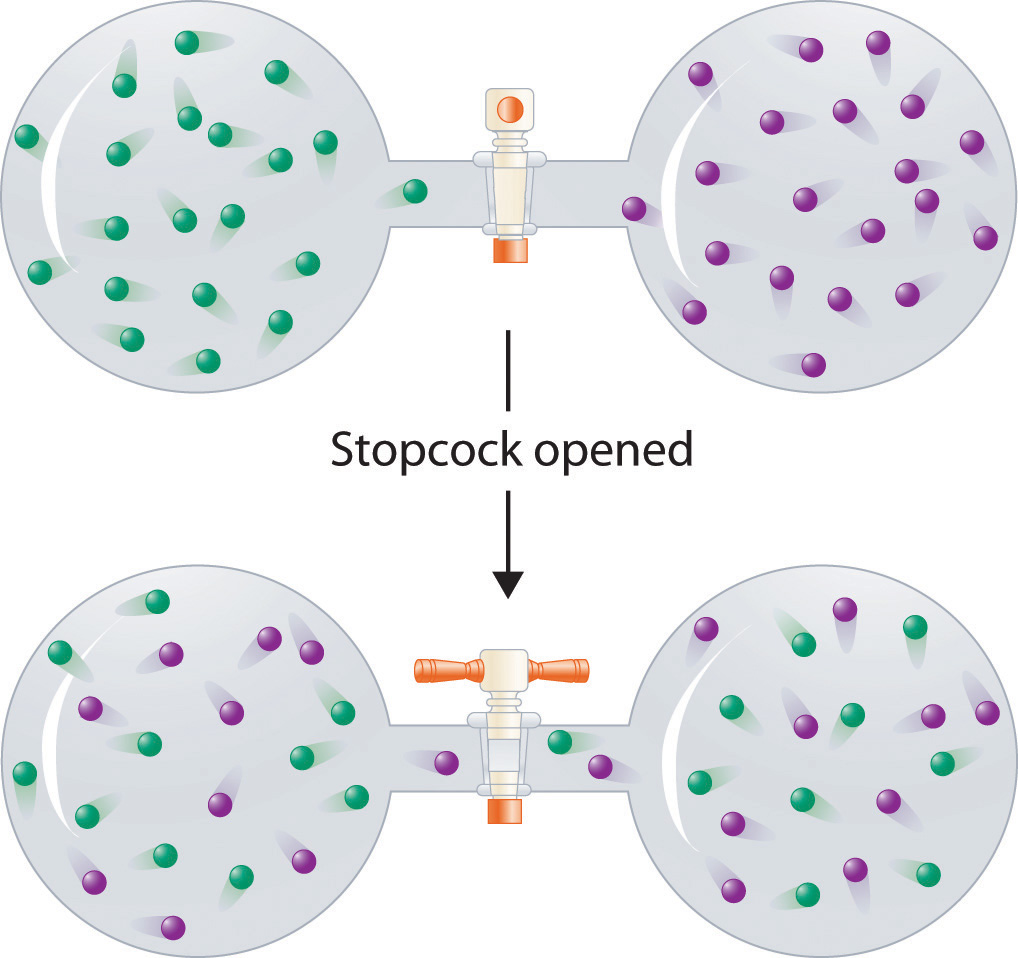
(top) Pure samples of two different gases are in separate bulbs. (bottom) When the connecting stopcock is opened, diffusion causes the two gases to mix together and form a solution. Even though ΔHsoln is zero for the process, the increased entropy of the solution (the increased disorder) versus that of the separate gases favors solution formation.
Example 1
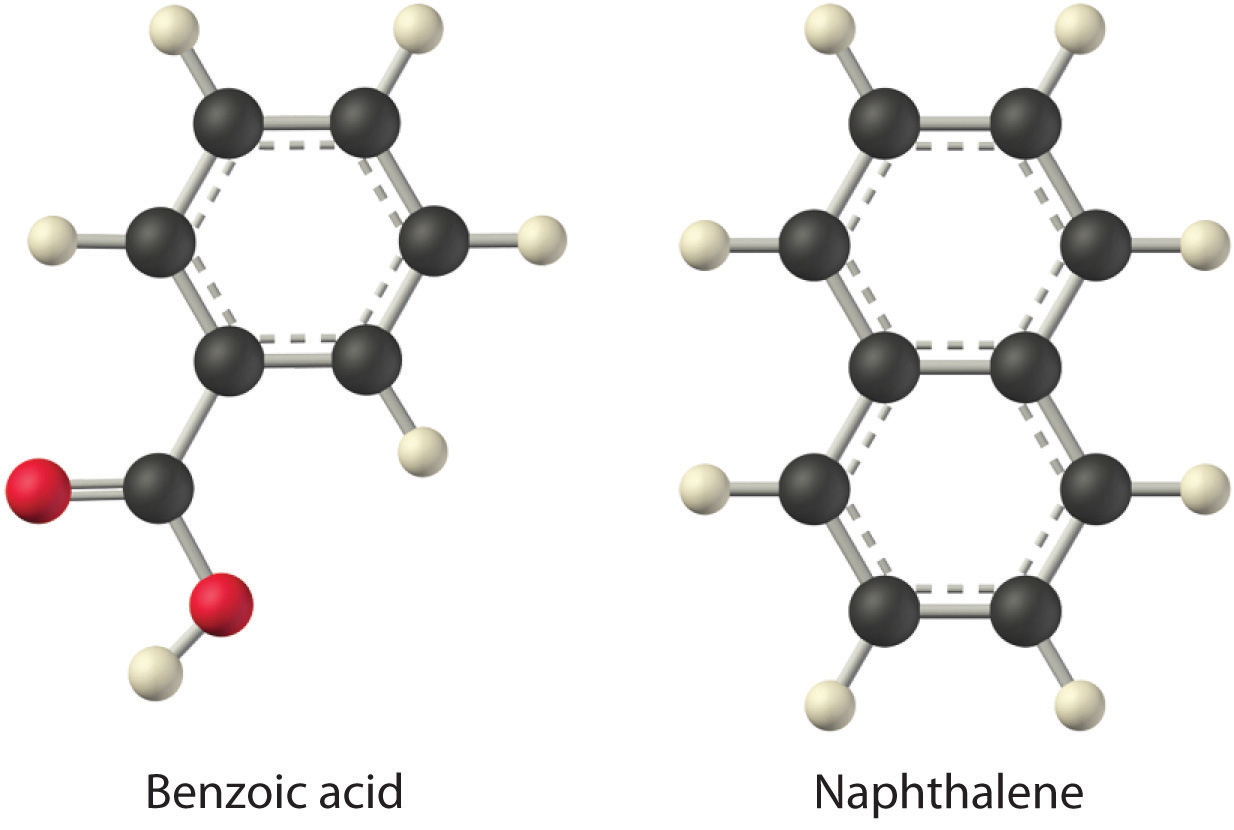
Considering LiCl, benzoic acid (C6H5CO2H), and naphthalene, which will be most soluble and which will be least soluble in water?
Given: three compounds
Asked for: relative solubilities in water
Strategy:
Assess the relative magnitude of the enthalpy change for each step in the process shown in Figure 13.1 "Enthalpy Changes That Accompany the Formation of a Solution". Then use Table 13.2 "Relative Changes in Enthalpies for Different Solute–Solvent Combinations*" to predict the solubility of each compound in water and arrange them in order of decreasing solubility.
Solution:
The first substance, LiCl, is an ionic compound, so a great deal of energy is required to separate its anions and cations and overcome the lattice energy (ΔH2 is far greater than zero in Equation 13.3). Because water is a polar substance, the interactions between both Li+ and Cl− ions and water should be favorable and strong. Thus we expect ΔH3 to be far less than zero, making LiCl soluble in water. In contrast, naphthalene is a nonpolar compound, with only London dispersion forces holding the molecules together in the solid state. We therefore expect ΔH2 to be small and positive. We also expect the interaction between polar water molecules and nonpolar naphthalene molecules to be weak ΔH3 ≈ 0. Hence we do not expect naphthalene to be very soluble in water, if at all. Benzoic acid has a polar carboxylic acid group and a nonpolar aromatic ring. We therefore expect that the energy required to separate solute molecules (ΔH2) will be greater than for naphthalene and less than for LiCl. The strength of the interaction of benzoic acid with water should also be intermediate between those of LiCl and naphthalene. Hence benzoic acid is expected to be more soluble in water than naphthalene but less soluble than LiCl. We thus predict LiCl to be the most soluble in water and naphthalene to be the least soluble.
Exercise
Considering ammonium chloride, cyclohexane, and ethylene glycol (HOCH2CH2OH), which will be most soluble and which will be least soluble in benzene?
Answer: The most soluble is cyclohexane; the least soluble is ammonium chloride.
Summary
Solutions are homogeneous mixtures of two or more substances whose components are uniformly distributed on a microscopic scale. The component present in the greatest amount is the solvent, and the components present in lesser amounts are the solute(s). The formation of a solution from a solute and a solvent is a physical process, not a chemical one. Substances that are miscible, such as gases, form a single phase in all proportions when mixed. Substances that form separate phases are immiscible. Solvation is the process in which solute particles are surrounded by solvent molecules. When the solvent is water, the process is called hydration. The overall enthalpy change that accompanies the formation of a solution, ΔHsoln, is the sum of the enthalpy change for breaking the intermolecular interactions in both the solvent and the solute and the enthalpy change for the formation of new solute–solvent interactions. Exothermic (ΔHsoln < 0) processes favor solution formation. In addition, the change in entropy, the degree of disorder of the system, must be considered when predicting whether a solution will form. An increase in entropy (a decrease in order) favors dissolution.
Key Takeaway
- The magnitude of the changes in both enthalpy and entropy must be considered when predicting whether a given solute–solvent combination will spontaneously form a solution.
Conceptual Problems
-
Classify each of the following as a heterogeneous mixture or homogeneous mixture. Explain your rationale in each case.
- aqueous ammonia
- liquid decongestant
- vinegar
- seawater
- gasoline
- fog
-
Solutions and heterogeneous mixtures are at the extreme ends of the solubility scale. Name one type of mixture that is intermediate on this scale. How are the properties of the mixture you have chosen different from those of a solution or a heterogeneous mixture?
-
Classify each process as simple dissolution or a chemical reaction.
- a naphthalene mothball dissolving in benzene
- a sample of a common drain cleaner that has a mixture of NaOH crystals and Al chunks dissolving in water to give H2 gas and an aqueous solution of Na+, OH−, and Al3+ ions
- an iron ship anchor slowly dissolving in seawater
- sodium metal dissolving in liquid ammonia
-
Classify each process as simple dissolution or a chemical reaction.
- a sugar cube dissolving in a cup of hot tea
- SO3 gas dissolving in water to produce sulfuric acid
- calcium oxide dissolving in water to produce a basic solution
- metallic gold dissolving in a small quantity of liquid mercury
-
You notice that a gas is evolved as you are dissolving a solid in a liquid. Will you be able to recover your original solid by evaporation? Why or why not?
-
Why is heat evolved when sodium hydroxide pellets are dissolved in water? Does this process correspond to simple dissolution or a chemical reaction? Justify your answer.
-
Which process(es) is the simple formation of a solution, and which process(es) involves a chemical reaction?
- mixing an aqueous solution of NaOH with an aqueous solution of HCl
- bubbling HCl gas through water
- adding iodine crystals to CCl4
- adding sodium metal to ethanol to produce sodium ethoxide (C2H5O−Na+) and hydrogen gas
-
Using thermochemical arguments, explain why some substances that do not form a solution at room temperature will form a solution when heated. Explain why a solution can form even when ΔHsoln is positive.
-
If you wanted to formulate a new compound that could be used in an instant cold pack, would you select a compound with a positive or negative value of ΔHsoln in water? Justify your answer.
-
Why is entropy the dominant factor in the formation of solutions of two or more gases? Is it possible for two gases to be immiscible? Why or why not?
Answers
-
Homogeneous mixtures: aqueous ammonia, liquid decongestant, vinegar, and gasoline. Heterogeneous mixtures: seawater and fog.
-
-
-
-
-
-
All are chemical reactions except dissolving iodine crystals in CCl4.
-
-
-
13.2 Solubility and Molecular Structure
Learning Objective
- To understand the relationship between solubility and molecular structure.
When a solute dissolves, its individual atoms, molecules, or ions interact with the solvent, become solvated, and are able to diffuse independently throughout the solution (part (a) in Figure 13.4 "Dissolution and Precipitation"). This is not, however, a unidirectional process. If the molecule or ion happens to collide with the surface of a particle of the undissolved solute, it may adhere to the particle in a process called crystallization. Dissolution and crystallization continue as long as excess solid is present, resulting in a dynamic equilibrium analogous to the equilibrium that maintains the vapor pressure of a liquid. (For more information about vapor pressure, see Chapter 11 "Liquids", Section 11.3 "Unique Properties of Liquids".) We can represent these opposing processes as follows:
Equation 13.4
Although the terms precipitation and crystallization are both used to describe the separation of solid solute from a solution, crystallization refers to the formation of a solid with a well-defined crystalline structure, whereas precipitation refers to the formation of any solid phase, often one with very small particles.
Figure 13.4 Dissolution and Precipitation
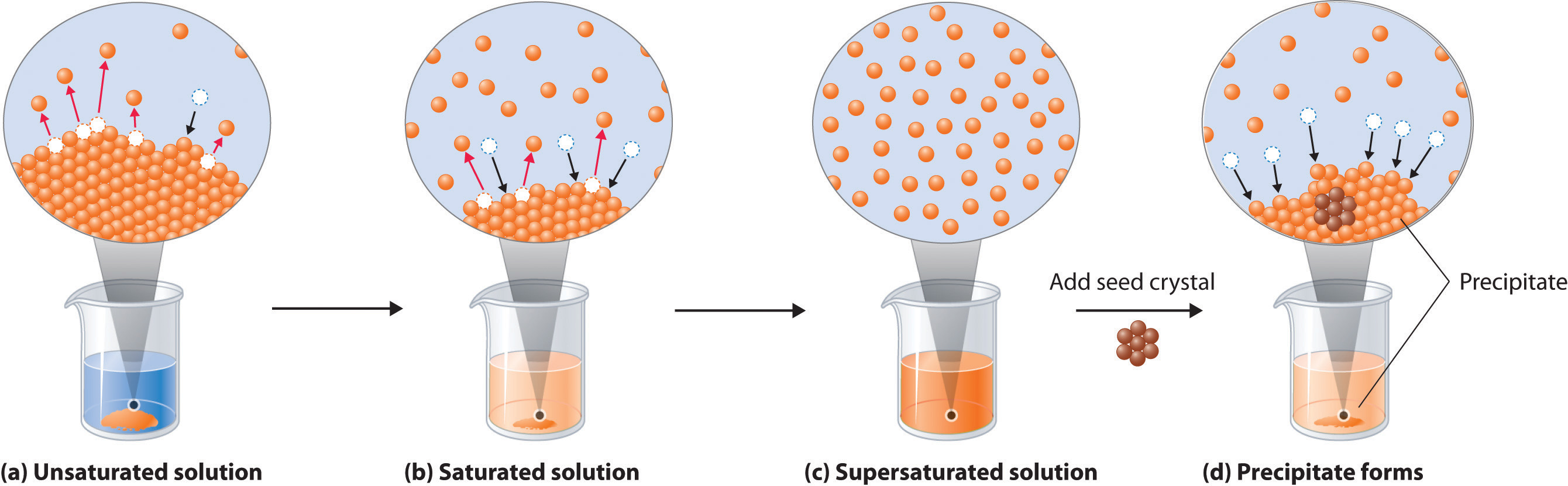
(a) When a solid is added to a solvent in which it is soluble, solute particles leave the surface of the solid and become solvated by the solvent, initially forming an unsaturated solution. (b) When the maximum possible amount of solute has dissolved, the solution becomes saturated. If excess solute is present, the rate at which solute particles leave the surface of the solid equals the rate at which they return to the surface of the solid. (c) A supersaturated solution can usually be formed from a saturated solution by filtering off the excess solute and lowering the temperature. (d) When a seed crystal of the solute is added to a supersaturated solution, solute particles leave the solution and form a crystalline precipitate.
Factors Affecting Solubility
The maximum amount of a solute that can dissolve in a solvent at a specified temperature and pressure is its solubilityA measure of the how much of a solid substance remains dissolved in a given amount of a specified liquid at a specified temperature and pressure.. Solubility is often expressed as the mass of solute per volume (g/L) or mass of solute per mass of solvent (g/g), or as the moles of solute per volume (mol/L). Even for very soluble substances, however, there is usually a limit to how much solute can dissolve in a given quantity of solvent. In general, the solubility of a substance depends on not only the energetic factors we have discussed but also the temperature and, for gases, the pressure. At 20°C, for example, 177 g of NaI, 91.2 g of NaBr, 35.9 g of NaCl, and only 4.1 g of NaF dissolve in 100 g of water. At 70°C, however, the solubilities increase to 295 g of NaI, 119 g of NaBr, 37.5 g of NaCl, and 4.8 g of NaF. As you learned in Chapter 12 "Solids", the lattice energies of the sodium halides increase from NaI to NaF. The fact that the solubilities decrease as the lattice energy increases suggests that the ΔH2 term in Figure 13.1 "Enthalpy Changes That Accompany the Formation of a Solution" dominates for this series of compounds.
A solution with the maximum possible amount of solute is saturatedA solution with the maximum possible amount of a solute under a given set of conditions.. If a solution contains less than the maximum amount of solute, it is unsaturated. When a solution is saturated and excess solute is present, the rate of dissolution is exactly equal to the rate of crystallization (part (b) in Figure 13.4 "Dissolution and Precipitation"). Using the value just stated, a saturated aqueous solution of NaCl, for example, contains 35.9 g of NaCl per 100 mL of water at 20°C. We can prepare a homogeneous saturated solution by adding excess solute (in this case, greater than 35.9 g of NaCl) to the solvent (water), stirring until the maximum possible amount of solute has dissolved, and then removing undissolved solute by filtration.
Note the Pattern
The solubility of most solids increases with increasing temperature.
Because the solubility of most solids increases with increasing temperature, a saturated solution that was prepared at a higher temperature usually contains more dissolved solute than it would contain at a lower temperature. When the solution is cooled, it can therefore become supersaturatedAn unstable solution with more dissolved solute than it would normally contain under the given set of conditions. (part (c) in Figure 13.4 "Dissolution and Precipitation"). Like a supercooled or superheated liquid (see Chapter 11 "Liquids"), a supersaturated solution is unstable. Consequently, adding a small particle of the solute, a seed crystalA solid sample of a substance that can be added to a supercooled liquid or a supersaturated solution to help induce crystallization., will usually cause the excess solute to rapidly precipitate or crystallize, sometimes with spectacular results, as was shown in Figure 1.9 "The Crystallization of Sodium Acetate from a Concentrated Solution of Sodium Acetate in Water". The rate of crystallization in Equation 13.4 is greater than the rate of dissolution, so crystals or a precipitate form (part (d) in Figure 13.4 "Dissolution and Precipitation"). In contrast, adding a seed crystal to a saturated solution reestablishes the dynamic equilibrium, and the net quantity of dissolved solute no longer changes.
Because crystallization is the reverse of dissolution, a substance that requires an input of heat to form a solution (ΔHsoln > 0) releases that heat when it crystallizes from solution (ΔHcrys < 0). The amount of heat released is proportional to the amount of solute that exceeds its solubility. Two substances that have a positive enthalpy of solution are sodium thiosulfate (Na2S2O3) and sodium acetate (CH3CO2Na), both of which are used in commercial hot packs, small bags of supersaturated solutions used to warm hands (see Figure 5.13 "The High Specific Heat of Liquid Water Has Major Effects on Climate").
Interactions in Liquid Solutions
The interactions that determine the solubility of a substance in a liquid depend largely on the chemical nature of the solute (such as whether it is ionic or molecular) rather than on its physical state (solid, liquid, or gas). We will first describe the general case of forming a solution of a molecular species in a liquid solvent and then describe the formation of a solution of an ionic compound.
Solutions of Molecular Substances in Liquids
The London dispersion forces, dipole–dipole interactions, and hydrogen bonds that hold molecules to other molecules are generally weak. Even so, energy is required to disrupt these interactions. As we described in Section 13.1 "Factors Affecting Solution Formation", unless some of that energy is recovered in the formation of new, favorable solute–solvent interactions, the increase in entropy on solution formation is not enough for a solution to form.
For solutions of gases in liquids, we can safely ignore the energy required to separate the solute molecules (ΔH2 = 0) because the molecules are already separated. Thus we need to consider only the energy required to separate the solvent molecules (ΔH1) and the energy released by new solute–solvent interactions (ΔH3). Nonpolar gases such as N2, O2, and Ar have no dipole moment and cannot engage in dipole–dipole interactions or hydrogen bonding. Consequently, the only way they can interact with a solvent is by means of London dispersion forces, which may be weaker than the solvent–solvent interactions in a polar solvent. It is not surprising, then, that nonpolar gases are most soluble in nonpolar solvents. In this case, ΔH1 and ΔH3 are both small and of similar magnitude. In contrast, for a solution of a nonpolar gas in a polar solvent, ΔH1 is far greater than ΔH3. As a result, nonpolar gases are less soluble in polar solvents than in nonpolar solvents. For example, the concentration of N2 in a saturated solution of N2 in water, a polar solvent, is only 7.07 × 10−4 M compared with 4.5 × 10−3 M for a saturated solution of N2 in benzene, a nonpolar solvent.
The solubilities of nonpolar gases in water generally increase as the molecular mass of the gas increases, as shown in Table 13.3 "Solubilities of Selected Gases in Water at 20°C and 1 atm Pressure". This is precisely the trend expected: as the gas molecules become larger, the strength of the solvent–solute interactions due to London dispersion forces increases, approaching the strength of the solvent–solvent interactions.
Table 13.3 Solubilities of Selected Gases in Water at 20°C and 1 atm Pressure
| Gas | Solubility (M) × 10−4 |
|---|---|
| He | 3.90 |
| Ne | 4.65 |
| Ar | 15.2 |
| Kr | 27.9 |
| Xe | 50.2 |
| H2 | 8.06 |
| N2 | 7.07 |
| CO | 10.6 |
| O2 | 13.9 |
| N2O | 281 |
| CH4 | 15.5 |
Virtually all common organic liquids, whether polar or not, are miscible. The strengths of the intermolecular attractions are comparable; thus the enthalpy of solution is expected to be small (ΔHsoln ≈ 0), and the increase in entropy drives the formation of a solution. If the predominant intermolecular interactions in two liquids are very different from one another, however, they may be immiscible. For example, organic liquids such as benzene, hexane, CCl4, and CS2 (S=C=S) are nonpolar and have no ability to act as hydrogen bond donors or acceptors with hydrogen-bonding solvents such as H2O, HF, and NH3; hence they are immiscible in these solvents. When shaken with water, they form separate phases or layers separated by an interface (Figure 13.5 "Immiscible Liquids"), the region between the two layers. Just because two liquids are immiscible, however, does not mean that they are completely insoluble in each other. For example, 188 mg of benzene dissolves in 100 mL of water at 23.5°C. Adding more benzene results in the separation of an upper layer consisting of benzene with a small amount of dissolved water (the solubility of water in benzene is only 178 mg/100 mL of benzene).
Figure 13.5 Immiscible Liquids
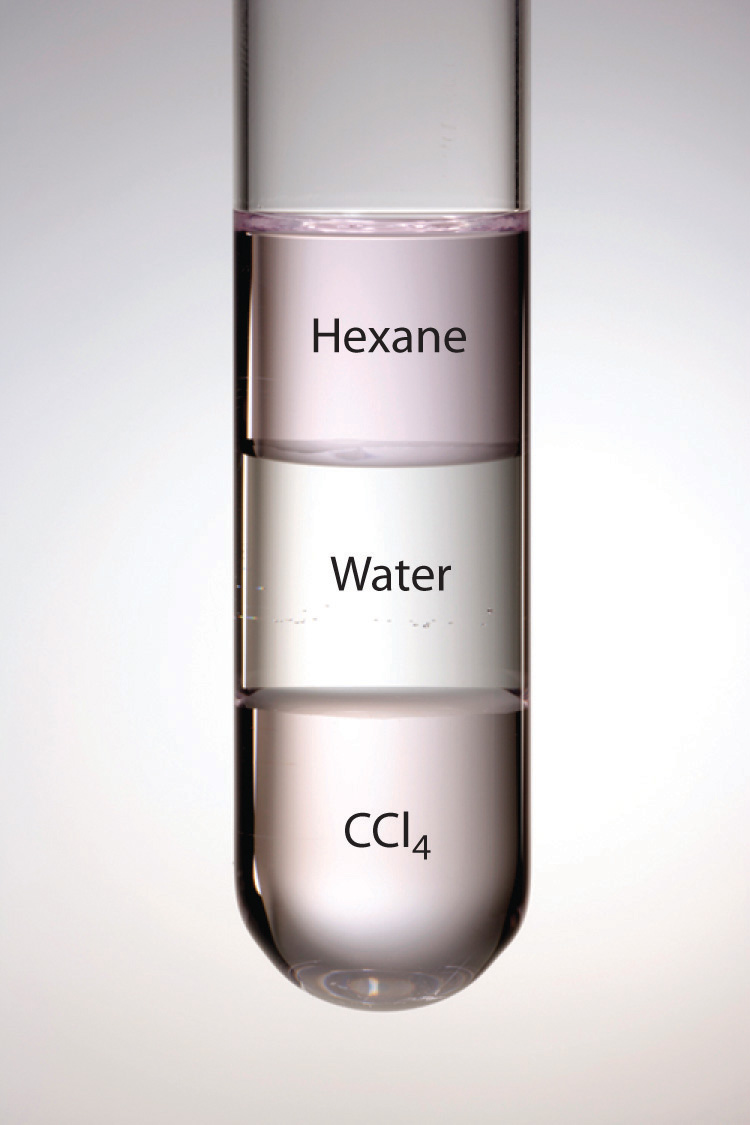
Water is immiscible with both CCl4 and hexane. When all three liquids are mixed, they separate into three distinct layers. Because water is less dense than CCl4, the water layer floats on the CCl4. In contrast, hexane is less dense than water, so the hexane floats on the water layer. Because I2 is intensely purple and quite soluble in both CCl4 and hexane, but insoluble in water, a small amount of I2 has been added to help identify the hexane and CCl4 layers.
The solubilities of simple alcohols in water are given in Table 13.4 "Solubilities of Straight-Chain Organic Alcohols in Water at 20°C". Only the three lightest alcohols (methanol, ethanol, and n-propanol) are completely miscible with water. As the molecular mass of the alcohol increases, so does the proportion of hydrocarbon in the molecule. Correspondingly, the importance of hydrogen bonding and dipole–dipole interactions in the pure alcohol decreases, while the importance of London dispersion forces increases, which leads to progressively fewer favorable electrostatic interactions with water. Organic liquids such as acetone, ethanol, and tetrahydrofuran are sufficiently polar to be completely miscible with water yet sufficiently nonpolar to be completely miscible with all organic solvents.
Table 13.4 Solubilities of Straight-Chain Organic Alcohols in Water at 20°C
| Alcohol | Solubility (mol/100 g of H2O) |
|---|---|
| methanol | completely miscible |
| ethanol | completely miscible |
| n-propanol | completely miscible |
| n-butanol | 0.11 |
| n-pentanol | 0.030 |
| n-hexanol | 0.0058 |
| n-heptanol | 0.0008 |
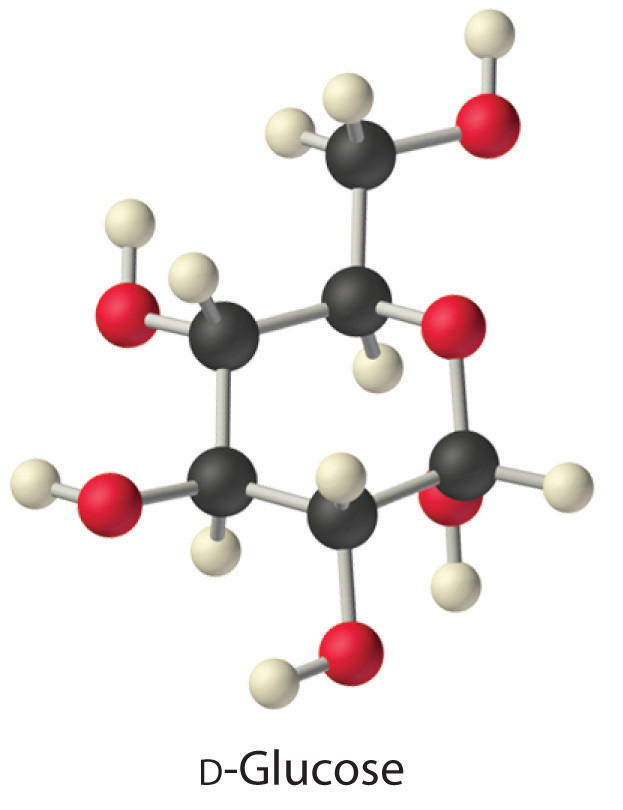
The same principles govern the solubilities of molecular solids in liquids. For example, elemental sulfur is a solid consisting of cyclic S8 molecules that have no dipole moment. Because the S8 rings in solid sulfur are held to other rings by London dispersion forces, elemental sulfur is insoluble in water. It is, however, soluble in nonpolar solvents that have comparable London dispersion forces, such as CS2 (23 g/100 mL). In contrast, glucose contains five –OH groups that can form hydrogen bonds. Consequently, glucose is very soluble in water (91 g/120 mL of water) but essentially insoluble in nonpolar solvents such as benzene. The structure of one isomer of glucose is shown here.
Low-molecular-mass hydrocarbons with highly electronegative and polarizable halogen atoms, such as chloroform (CHCl3) and methylene chloride (CH2Cl2), have both significant dipole moments and relatively strong London dispersion forces. These hydrocarbons are therefore powerful solvents for a wide range of polar and nonpolar compounds. Naphthalene, which is nonpolar, and phenol (C6H5OH), which is polar, are very soluble in chloroform. In contrast, the solubility of ionic compounds is largely determined not by the polarity of the solvent but rather by its dielectric constant, a measure of its ability to separate ions in solution, as you will soon see.
Example 2
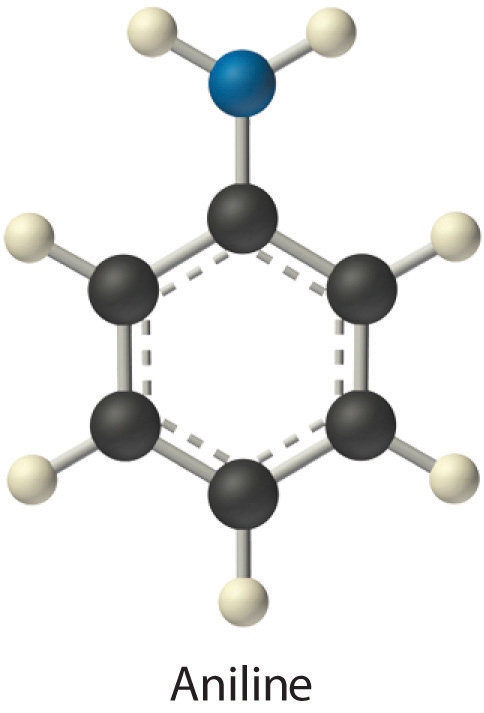
Identify the most important solute–solvent interactions in each solution.
- iodine in benzene
-
aniline (C6H5NH2) in dichloromethane (CH2Cl2)
- iodine in water
Given: components of solutions
Asked for: predominant solute–solvent interactions
Strategy:
Identify all possible intermolecular interactions for both the solute and the solvent: London dispersion forces, dipole–dipole interactions, or hydrogen bonding. Determine which is likely to be the most important factor in solution formation.
Solution:
- Benzene and I2 are both nonpolar molecules. The only possible attractive forces are London dispersion forces.
- Aniline is a polar molecule with an –NH2 group, which can act as a hydrogen bond donor. Dichloromethane is also polar, but it has no obvious hydrogen bond acceptor. Therefore, the most important interactions between aniline and CH2Cl2 are likely to be London interactions.
- Water is a highly polar molecule that engages in extensive hydrogen bonding, whereas I2 is a nonpolar molecule that cannot act as a hydrogen bond donor or acceptor. The slight solubility of I2 in water (1.3 × 10−3 mol/L at 25°C) is due to London dispersion forces.
Exercise
Identify the most important interactions in each solution:
- ethylene glycol (HOCH2CH2OH) in acetone
- acetonitrile (CH3C≡N) in acetone
- n-hexane in benzene
Answer:
- hydrogen bonding
- London interactions
- London dispersion forces
Hydrophilic and Hydrophobic Solutes
A solute can be classified as hydrophilicA substance attracted to water. Hydrophilic substances are polar and can form hydrogen bonds to water. (literally, “water loving”), meaning that it has an electrostatic attraction to water, or hydrophobicA substance that repels water. Hydrophobic substances do not interact favorably with water. (“water fearing”), meaning that it repels water. A hydrophilic substance is polar and often contains O–H or N–H groups that can form hydrogen bonds to water. For example, glucose with its five O–H groups is hydrophilic. In contrast, a hydrophobic substance may be polar but usually contains C–H bonds that do not interact favorably with water, as is the case with naphthalene and n-octane. Hydrophilic substances tend to be very soluble in water and other strongly polar solvents, whereas hydrophobic substances are essentially insoluble in water and soluble in nonpolar solvents such as benzene and cyclohexane.
The difference between hydrophilic and hydrophobic substances has substantial consequences in biological systems. For example, vitamins can be classified as either fat soluble or water soluble. Fat-soluble vitamins, such as vitamin A, are mostly nonpolar, hydrophobic molecules. As a result, they tend to be absorbed into fatty tissues and stored there. In contrast, water-soluble vitamins, such as vitamin C, are polar, hydrophilic molecules that circulate in the blood and intracellular fluids, which are primarily aqueous. Water-soluble vitamins are therefore excreted much more rapidly from the body and must be replenished in our daily diet. A comparison of the chemical structures of vitamin A and vitamin C quickly reveals why one is hydrophobic and the other hydrophilic.
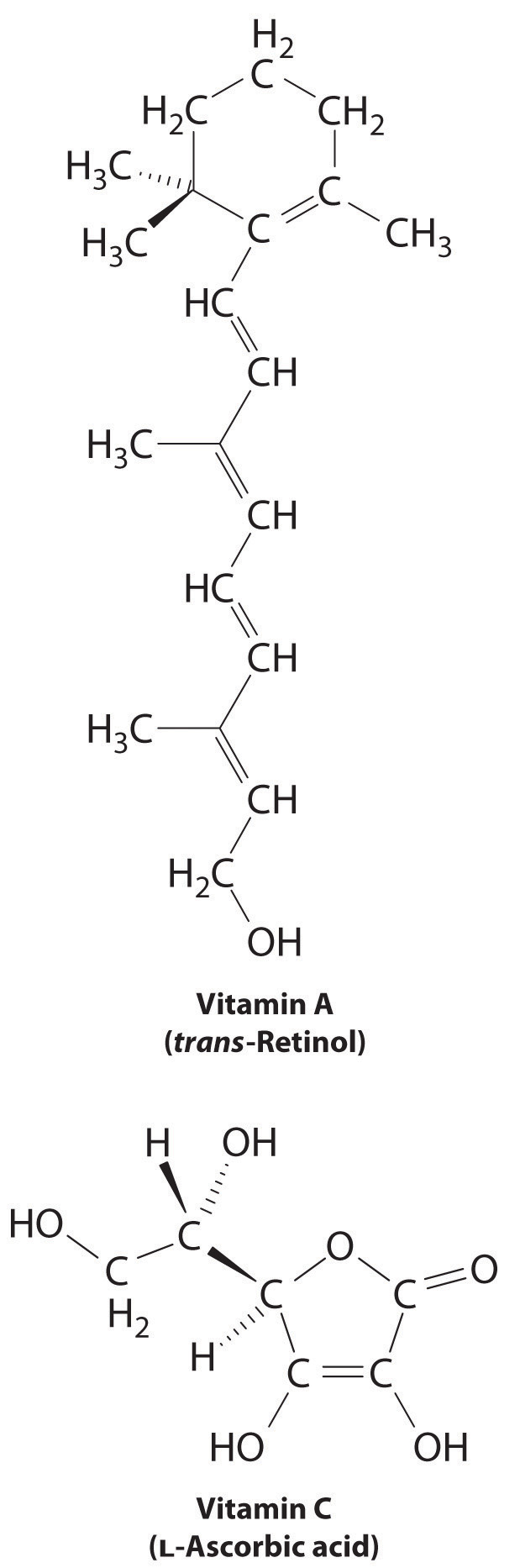
Because water-soluble vitamins are rapidly excreted, the risk of consuming them in excess is relatively small. Eating a dozen oranges a day is likely to make you tired of oranges long before you suffer any ill effects due to their high vitamin C content. In contrast, fat-soluble vitamins constitute a significant health hazard when consumed in large amounts. For example, the livers of polar bears and other large animals that live in cold climates contain large amounts of vitamin A, which have occasionally proven fatal to humans who have eaten them.
Example 3
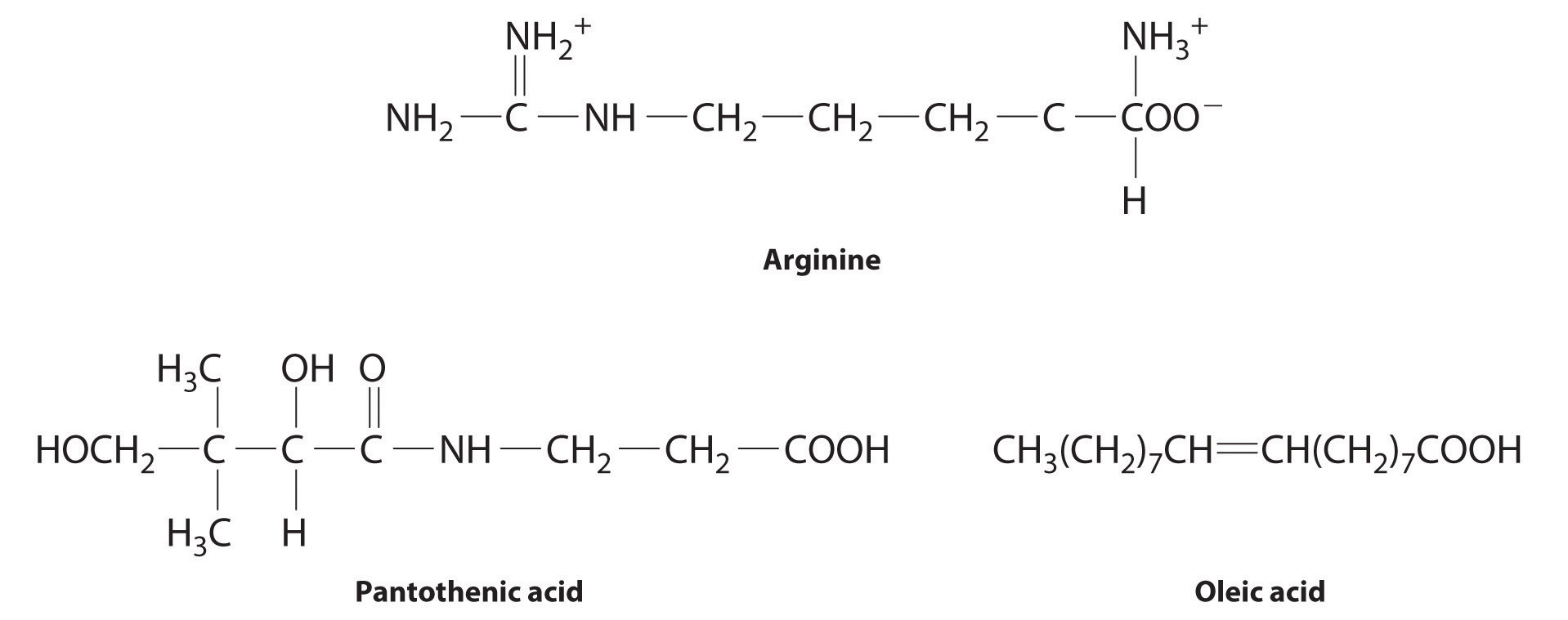
The following substances are essential components of the human diet:
Using what you know of hydrophilic and hydrophobic solutes, classify each as water soluble or fat soluble and predict which are likely to be required in the diet on a daily basis.
- arginine
- pantothenic acid
- oleic acid
Given: chemical structures
Asked for: classification as water soluble or fat soluble; dietary requirement
Strategy:
Based on the structure of each compound, decide whether it is hydrophilic or hydrophobic. If it is hydrophilic, it is likely to be required on a daily basis.
Solution:
- Arginine is a highly polar molecule with two positively charged groups and one negatively charged group, all of which can form hydrogen bonds with water. As a result, it is hydrophilic and required in our daily diet.
- Although pantothenic acid contains a hydrophobic hydrocarbon portion, it also contains several polar functional groups (–OH and –CO2H) that should interact strongly with water. It is therefore likely to be water soluble and required in the diet. (In fact, pantothenic acid is almost always a component of multiple-vitamin tablets.)
- Oleic acid is a hydrophobic molecule with a single polar group at one end. It should be fat soluble and not required daily.
Exercise
These compounds are consumed by humans: caffeine, acetaminophen, and vitamin D. Identify each as primarily hydrophilic (water soluble) or hydrophobic (fat soluble), and predict whether each is likely to be excreted from the body rapidly or slowly.
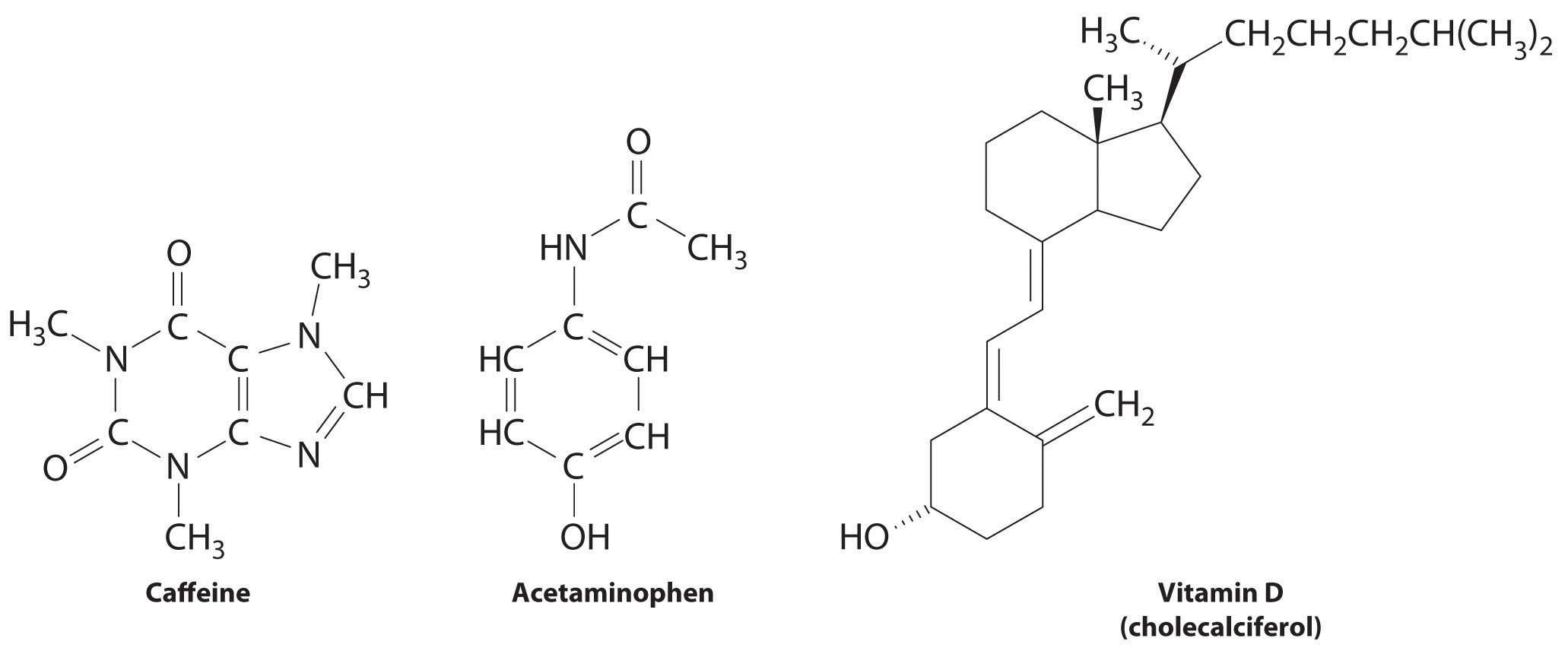
Answer: Caffeine and acetaminophen are water soluble and rapidly excreted, whereas vitamin D is fat soluble and slowly excreted.
Solid Solutions
Solutions are not limited to gases and liquids; solid solutions also exist. For example, amalgamsA solution (usually a solid solution) of a metal in liquid mercury., which are usually solids, are solutions of metals in liquid mercury. Because most metals are soluble in mercury, amalgams are used in gold mining, dentistry, and many other applications. A major difficulty when mining gold is separating very small particles of pure gold from tons of crushed rock. One way to accomplish this is to agitate a suspension of the crushed rock with liquid mercury, which dissolves the gold (as well as any metallic silver that might be present). The very dense liquid gold–mercury amalgam is then isolated and the mercury distilled away.
An alloy is a solid or liquid solution that consists of one or more elements in a metallic matrix. A solid alloy has a single homogeneous phase in which the crystal structure of the solvent remains unchanged by the presence of the solute. Thus the microstructure of the alloy is uniform throughout the sample. Examples are substitutional and interstitial alloys such as brass or solder. (For more information about alloys, see Chapter 12 "Solids", Section 12.5 "Correlation between Bonding and the Properties of Solids") Liquid alloys include sodium/potassium and gold/mercury. In contrast, a partial alloy solution has two or more phases that can be homogeneous in the distribution of the components, but the microstructures of the two phases are not the same. As a liquid solution of lead and tin is cooled, for example, different crystalline phases form at different cooling temperatures. As you learned in Chapter 12 "Solids", alloys usually have properties that differ from those of the component elements.
Network solids such as diamond, graphite, and SiO2 are insoluble in all solvents with which they do not react chemically. The covalent bonds that hold the network or lattice together are simply too strong to be broken under normal conditions. They are certainly much stronger than any conceivable combination of intermolecular interactions that might occur in solution. Most metals are insoluble in virtually all solvents for the same reason: the delocalized metallic bonding is much stronger than any favorable metal atom–solvent interactions. Many metals react with solutions such as aqueous acids or bases to produce a solution. However, as we saw in Section 13.1 "Factors Affecting Solution Formation", in these instances the metal undergoes a chemical transformation that cannot be reversed by simply removing the solvent.
Note the Pattern
Solids with very strong intermolecular bonding tend to be insoluble.
Solubilities of Ionic Substances in Liquids
Table 4.1 "Common Units of Concentration" introduced you to guidelines for predicting the solubility of ionic compounds in water. Ionic substances are generally most soluble in polar solvents; the higher the lattice energy, the more polar the solvent must be to overcome the lattice energy and dissolve the substance. Because of its high polarity, water is the most common solvent for ionic compounds. Many ionic compounds are soluble in other polar solvents, however, such as liquid ammonia, liquid hydrogen fluoride, and methanol. Because all these solvents consist of molecules that have relatively large dipole moments, they can interact favorably with the dissolved ions.
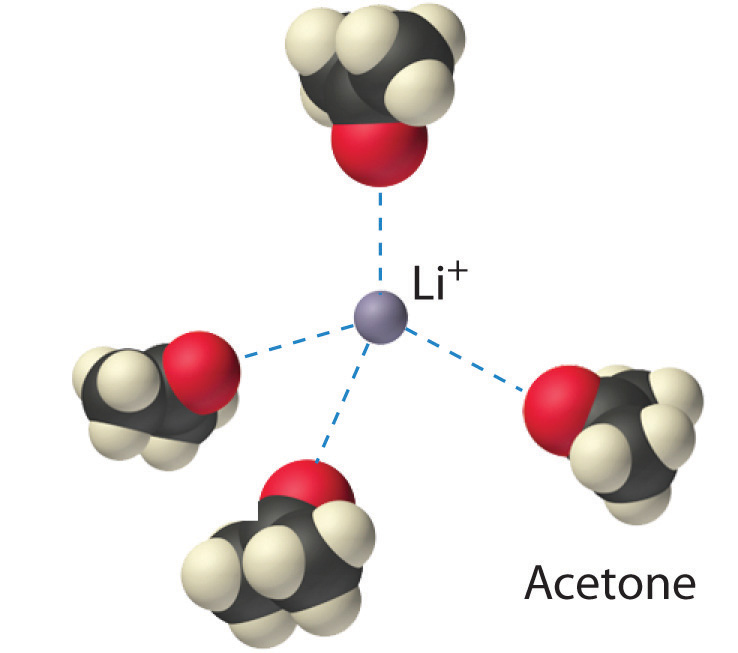
The interaction of water with Na+ and Cl− ions in an aqueous solution of NaCl was illustrated in Figure 4.3 "The Dissolution of Sodium Chloride in Water". The ion–dipole interactions between Li+ ions and acetone molecules in a solution of LiCl in acetone are shown in Figure 13.6 "Ion–Dipole Interactions in the Solvation of Li". The energetically favorable Li+–acetone interactions make ΔH3 in Figure 13.1 "Enthalpy Changes That Accompany the Formation of a Solution" sufficiently negative to overcome the positive ΔH1 and ΔH2. Because the dipole moment of acetone (2.88 D), and thus its polarity, is actually larger than that of water (1.85 D), one might even expect that LiCl would be more soluble in acetone than in water. In fact, the opposite is true: 83 g of LiCl dissolve in 100 mL of water at 20°C, but only about 4.1 g of LiCl dissolve in 100 mL of acetone. This apparent contradiction arises from the fact that the dipole moment is a property of a single molecule in the gas phase. A more useful measure of the ability of a solvent to dissolve ionic compounds is its dielectric constant (ε)A constant that expresses the ability of a bulk substance to decrease the electrostatic forces between two charged particles., which is the ability of a bulk substance to decrease the electrostatic forces between two charged particles. By definition, the dielectric constant of a vacuum is 1. In essence, a solvent with a high dielectric constant causes the charged particles to behave as if they have been moved farther apart. At 25°C, the dielectric constant of water is 80.1, one of the highest known, and that of acetone is only 21.0. Hence water is better able to decrease the electrostatic attraction between Li+ and Cl− ions, so LiCl is more soluble in water than in acetone. This behavior is in contrast to that of molecular substances, for which polarity is the dominant factor governing solubility.
Note the Pattern
A solvent’s dielectric constant is the most useful measure of its ability to dissolve ionic compounds. A solvent’s polarity is the dominant factor in dissolving molecular substances.
Figure 13.6 Ion–Dipole Interactions in the Solvation of Li+ Ions by Acetone, a Polar Solvent
It is also possible to dissolve ionic compounds in organic solvents using crown ethersCyclic polyether with four or more oxygen atoms separated by two or three carbon atoms. All crown ethers have a central cavity that can accommodate a metal ion coordinated to the ring of oxygen atoms., cyclic compounds with the general formula (OCH2CH2)n. Crown ethers are named using both the total number of atoms in the ring and the number of oxygen atoms. Thus 18-crown-6 is an 18-membered ring with six oxygen atoms (part (a) in Figure 13.7 "Crown Ethers and Cryptands"). The cavity in the center of the crown ether molecule is lined with oxygen atoms and is large enough to be occupied by a cation, such as K+. The cation is stabilized by interacting with lone pairs of electrons on the surrounding oxygen atoms. Thus crown ethers solvate cations inside a hydrophilic cavity, whereas the outer shell, consisting of C–H bonds, is hydrophobic. Crown ethers are useful for dissolving ionic substances such as KMnO4 in organic solvents such as isopropanol [(CH3)2CHOH] (Figure 13.8 "Effect of a Crown Ether on the Solubility of KMnO"). The availability of crown ethers with cavities of different sizes allows specific cations to be solvated with a high degree of selectivity.
Figure 13.7 Crown Ethers and Cryptands
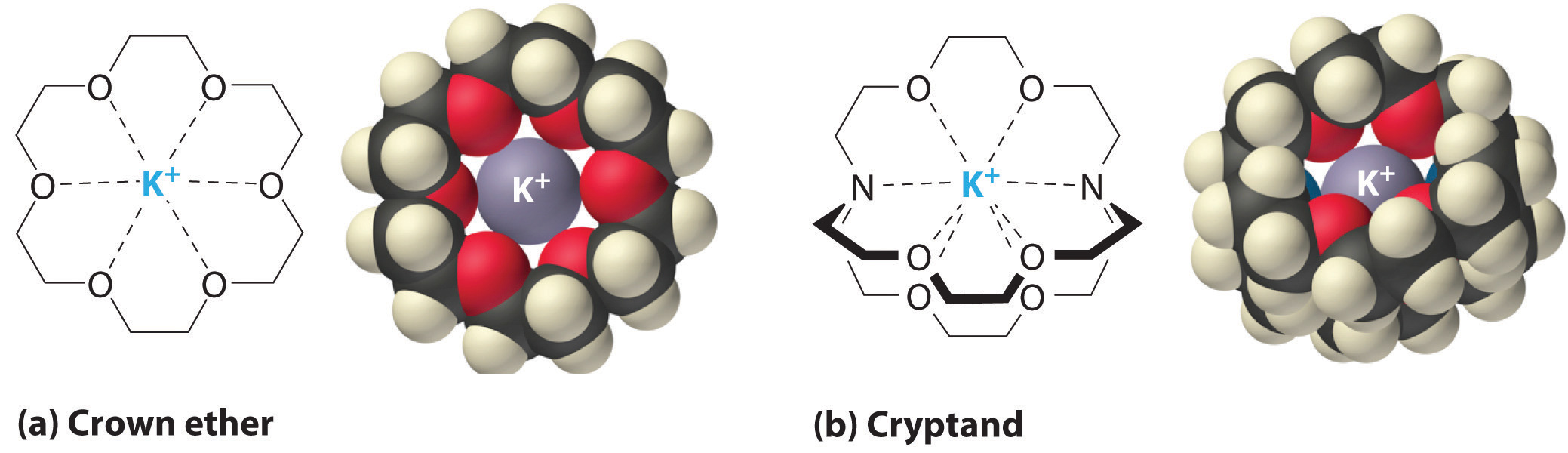
(a) The potassium complex of the crown ether 18-crown-6. Note how the cation is nestled within the central cavity of the molecule and interacts with lone pairs of electrons on the oxygen atoms. (b) The potassium complex of 2,2,2-cryptand, showing how the cation is almost hidden by the cryptand. Cryptands solvate cations via lone pairs of electrons on both oxygen and nitrogen atoms.
Figure 13.8 Effect of a Crown Ether on the Solubility of KMnO4 in Isopropanol (2-Propanol)

(a) Normally KMnO4, which is intensely purple, is completely insoluble in isopropanol, which has a relatively low dielectric constant. (b) In the presence of a small amount of 18-crown-6, KMnO4 dissolves in isopropanol, as shown by the reddish-purple color caused by permanganate ions in solution.
CryptandsConsisting of three chains connected by two nitrogen atoms, cryptands have a central cavity that can encapsulate a metal ion coordinated to the oxygen and nitrogen atoms. (from the Greek kryptós, meaning “hidden”) are compounds that can completely surround a cation with lone pairs of electrons on oxygen and nitrogen atoms (part (b) in Figure 13.7 "Crown Ethers and Cryptands"). The number in the name of the cryptand is the number of oxygen atoms in each strand of the molecule. Like crown ethers, cryptands can be used to prepare solutions of ionic compounds in solvents that are otherwise too nonpolar to dissolve them.
Summary
The solubility of a substance is the maximum amount of a solute that can dissolve in a given quantity of solvent; it depends on the chemical nature of both the solute and the solvent and on the temperature and pressure. When a solution contains the maximum amount of solute that can dissolve under a given set of conditions, it is a saturated solution. Otherwise, it is unsaturated. Supersaturated solutions, which contain more dissolved solute than allowed under particular conditions, are not stable; the addition of a seed crystal, a small particle of solute, will usually cause the excess solute to crystallize. A system in which crystallization and dissolution occur at the same rate is in dynamic equilibrium. The solubility of a substance in a liquid is determined by intermolecular interactions, which also determine whether two liquids are miscible. Solutes can be classified as hydrophilic (water loving) or hydrophobic (water fearing). Vitamins with hydrophilic structures are water soluble, whereas those with hydrophobic structures are fat soluble. Many metals dissolve in liquid mercury to form amalgams. Covalent network solids and most metals are insoluble in nearly all solvents. The solubility of ionic compounds is largely determined by the dielectric constant (ε) of the solvent, a measure of its ability to decrease the electrostatic forces between charged particles. Solutions of many ionic compounds in organic solvents can be dissolved using crown ethers, cyclic polyethers large enough to accommodate a metal ion in the center, or cryptands, compounds that completely surround a cation.
Key Takeaway
- The strength of intramolecular bonding determines the solubility of a solute in a given solvent.
Conceptual Problems
-
If a compound is only slightly soluble in a particular solvent, what are the relative strengths of the solvent–solvent and solute–solute interactions versus the solute–solvent interactions?
-
Predict whether each of the following sets of conditions favors formation of a solution:
Intermolecular Attractive Forces (Solute) Intermolecular Attractive Forces (Solvent) ΔHsoln London dispersion hydrogen bonding slightly positive dipole–dipole hydrogen bonding very negative ionic dipole–dipole slightly positive ionic London dispersion positive -
Arrange the following liquids in order of increasing solubility in water: t-butanol [(CH3)3COH], benzene, ammonia, and heptane. Justify your answer.
-
Which compound in each pair will be more soluble in water? Explain your reasoning in each case.
- toluene (C7H8) or ethyl ether (C2H5OC2H5)
- chloroform (CHCl3) or acetone (CH3COCH3)
- carbon tetrachloride (CCl4) or tetrahydrofuran (C4H8O)
- CaCl2 or CH2Cl2
-
Which compound in each pair will be more soluble in benzene? Explain your reasoning in each case.
- cyclohexane or methanol
- I2 or MgCl2
- methylene chloride (CH2Cl2) or acetic acid
-
Two water-insoluble compounds—n-decylamine [CH3(CH2)9NH2] and n-decane—can be separated by the following procedure: The compounds are dissolved in a solvent such as toluene that is immiscible with water. When adding an aqueous HCl solution to the mixture and stirring vigorously, the HCl reacts with one of the compounds to produce a salt. When the stirring is stopped and the mixture is allowed to stand, two layers are formed. At this point, each layer contains only one of the two original compounds. After the layers are separated, adding aqueous NaOH to the aqueous layer liberates one of the original compounds, which can then be removed by stirring with a second portion of toluene to extract it from the water.
- Identify the compound that is present in each layer following the addition of HCl. Explain your reasoning.
- How can the original compounds be recovered from the toluene solution?
-
Bromine and iodine are both soluble in CCl4, but bromine is much more soluble. Why?
-
A solution is made by mixing 50.0 mL of liquid A with 75.0 mL of liquid B. Which is the solute, and which is the solvent? Is it valid to assume that the volume of the resulting solution will be 125 mL? Explain your answer.
-
The compounds NaI, NaBr, and NaCl are far more soluble in water than NaF, a substance that is used to fluoridate drinking water. In fact, at 25°C the solubility of NaI is 184 g/100 mL of water, versus only 4.2 g/100 mL of water for NaF. Why is sodium iodide so much more soluble in water? Do you expect KCl to be more soluble or less soluble in water than NaCl?
-
When water is mixed with a solvent with which it is immiscible, the two liquids usually form two separate layers. If the density of the nonaqueous solvent is 1.75 g/mL at room temperature, sketch the appearance of the heterogeneous mixture in a beaker and label which layer is which. If you were not sure of the density and the identity of the other liquid, how might you be able to identify which is the aqueous layer?
-
When two liquids are immiscible, the addition of a third liquid can occasionally be used to induce the formation of a homogeneous solution containing all three.
- Ethylene glycol (HOCH2CH2OH) and hexane are immiscible, but adding acetone [(CH3)2CO] produces a homogeneous solution. Why does adding a third solvent produce a homogeneous solution?
- Methanol and n-hexane are immiscible. Which of the following solvents would you add to create a homogeneous solution—water, n-butanol, or cyclohexane? Justify your choice.
-
Some proponents of vitamin therapy for combating illness encourage the consumption of large amounts of fat-soluble vitamins. Why can this be dangerous? Would it be as dangerous to consume large amounts of water-soluble vitamins? Why or why not?
-
Why are most metals insoluble in virtually all solvents?
-
Because sodium reacts violently with water, it is difficult to weigh out small quantities of sodium metal for a reaction due to its rapid reaction with small amounts of moisture in the air. Would a Na/Hg amalgam be as sensitive to moisture as metallic sodium? Why or why not? A Na/K alloy is a liquid at room temperature. Will it be more or less sensitive to moisture than solid Na or K?
-
Dental amalgams often contain high concentrations of Hg, which is highly toxic. Why isn’t dental amalgam toxic?
-
Arrange 2,2,3-trimethylpentane, 1-propanol, toluene (C7H8), and dimethyl sulfoxide [(CH3)2S=O] in order of increasing dipole moment. Explain your reasoning.
-
Arrange acetone, chloroform, cyclohexane, and 2-butanol in order of increasing dielectric constant. Explain your reasoning.
-
Dissolving a white crystalline compound in ethanol gave a blue solution. Evaporating the ethanol from the solution gave a bluish-crystalline product, which slowly transformed into the original white solid on standing in the air for several days. Explain what happened. How does the mass of the initial bluish solid compare with the mass of the white solid finally recovered?
-
You have been asked to develop a new drug that could be used to bind Fe3+ ions in patients who suffer from iron toxicity, allowing the bound iron to be excreted in the urine. Would you consider a crown ether or a cryptand to be a reasonable candidate for such a drug? Explain your answer.
-
Describe two different situations in which fractional crystallization will not work as a separation technique when attempting to isolate a single compound from a mixture.
-
You have been given a mixture of two compounds—A and B—and have been told to isolate pure A. You know that pure A has a lower solubility than pure B and that the solubilities of both A and B increase with temperature. Outline a procedure to isolate pure A. If B had the lower solubility, could you use the same procedure to isolate pure A? Why or why not?
Answers
-
-
-
-
-
-
-
London dispersion forces increase with increasing atomic mass. Iodine is a solid while bromine is a liquid due to the greater intermolecular interactions between the heavier iodine atoms. Iodine is less soluble than bromine in virtually all solvents because it requires more energy to separate I2 molecules than Br2 molecules.
-
-
-
-
- A third solvent with intermediate polarity and/or dielectric constant can effectively dissolve both of the immiscible solvents, creating a single liquid phase.
- n-butanol—it is intermediate in polarity between methanol and n-hexane, while water is more polar than either and cyclohexane is comparable to n-hexane.
-
-
-
-
In dental amalgam, the mercury atoms are locked in a solid phase that does not undergo corrosion under physiological conditions; hence, the mercury atoms cannot readily diffuse to the surface where they could vaporize or undergo chemical reaction.
-
-
-
-
-
-
Dissolve the mixture of A and B in a solvent in which they are both soluble when hot and relatively insoluble when cold, filter off any undissolved B, and cool slowly. Pure A should crystallize, while B stays in solution. If B were less soluble, it would be impossible to obtain pure A by this method in a single step, because some of the less soluble compound (B) will always be present in the solid that crystallizes from solution.
13.3 Units of Concentration
Learning Objective
- To describe the concentration of a solution in the way that is most appropriate for a particular problem or application.
There are several different ways to quantitatively describe the concentrationThe quantity of solute that is dissolved in a particular quantity of solvent or solution. of a solution. For example, molarity was introduced in Chapter 4 "Reactions in Aqueous Solution" as a useful way to describe solution concentrations for reactions that are carried out in solution. Mole fractions, introduced in Chapter 10 "Gases", are used not only to describe gas concentrations but also to determine the vapor pressures of mixtures of similar liquids. Example 4 reviews the methods for calculating the molarity and mole fraction of a solution when the masses of its components are known.
Example 4
Commercial vinegar is essentially a solution of acetic acid in water. A bottle of vinegar has 3.78 g of acetic acid per 100.0 g of solution. Assume that the density of the solution is 1.00 g/mL.
- What is its molarity?
- What is its mole fraction?
Given: mass of substance and mass and density of solution
Asked for: molarity and mole fraction
Strategy:
A Calculate the number of moles of acetic acid in the sample. Then calculate the number of liters of solution from its mass and density. Use these results to determine the molarity of the solution.
B Determine the mass of the water in the sample and calculate the number of moles of water. Then determine the mole fraction of acetic acid by dividing the number of moles of acetic acid by the total number of moles of substances in the sample.
Solution:
-
A The molarity is the number of moles of acetic acid per liter of solution. We can calculate the number of moles of acetic acid as its mass divided by its molar mass. The volume of the solution equals its mass divided by its density. The calculations follow:
This result makes intuitive sense. If 100.0 g of aqueous solution (equal to 100 mL) contains 3.78 g of acetic acid, then 1 L of solution will contain 37.8 g of acetic acid, which is a little more than mole. Keep in mind, though, that the mass and volume of a solution are related by its density; concentrated aqueous solutions often have densities greater than 1.00 g/mL.
-
B To calculate the mole fraction of acetic acid in the solution, we need to know the number of moles of both acetic acid and water. The number of moles of acetic acid is 0.0629 mol, as calculated in part (a). We know that 100.0 g of vinegar contains 3.78 g of acetic acid; hence the solution also contains (100.0 g − 3.78 g) = 96.2 g of water. We have
The mole fraction X of acetic acid is the ratio of the number of moles of acetic acid to the total number of moles of substances present:
This answer makes sense, too. There are approximately 100 times as many moles of water as moles of acetic acid, so the ratio should be approximately 0.01.
Exercise
A solution of HCl gas dissolved in water (sold commercially as “muriatic acid,” a solution used to clean masonry surfaces) has 20.22 g of HCl per 100.0 g of solution, and its density is 1.10 g/mL.
- What is its molarity?
- What is its mole fraction?
Answer:
- 6.10 M HCl
- XHCl = 0.111
The concentration of a solution can also be described by its molality (m)The number of moles of solute present in exactly 1 kg of solvent., the number of moles of solute per kilogram of solvent:
Equation 13.5
Molality, therefore, has the same numerator as molarity (the number of moles of solute) but a different denominator (kilogram of solvent rather than liter of solution). For dilute aqueous solutions, the molality and molarity are nearly the same because dilute solutions are mostly solvent. Thus because the density of water under standard conditions is very close to 1.0 g/mL, the volume of 1.0 kg of H2O under these conditions is very close to 1.0 L, and a 0.50 M solution of KBr in water, for example, has approximately the same concentration as a 0.50 m solution.
Another common way of describing concentration is as the ratio of the mass of the solute to the total mass of the solution. The result can be expressed as mass percentageThe ratio of the total mass of the solute to the total mass of the solution., parts per million (ppm)Milligrams of solute per kilogram of solvent., or parts per billion (ppb)Micrograms of solute per kilogram of solvent.:
Equation 13.6
Equation 13.7
Equation 13.8
In the health sciences, the concentration of a solution is typically expressed as parts per thousand (ppt)Grams of solute per kilogram of solvent, primarily used in the health sciences., indicated as a proportion. For example, adrenalin, the hormone produced in high-stress situations, is available in a 1:1000 solution, or one gram of adrenalin per 1000 g of solution.
The labels on bottles of commercial reagents often describe the contents in terms of mass percentage. Sulfuric acid, for example, is sold as a 95% aqueous solution, or 95 g of H2SO4 per 100 g of solution. Parts per million and parts per billion are used to describe concentrations of highly dilute solutions. These measurements correspond to milligrams and micrograms of solute per kilogram of solution, respectively. For dilute aqueous solutions, this is equal to milligrams and micrograms of solute per liter of solution (assuming a density of 1.0 g/mL).
Example 5
Several years ago, millions of bottles of mineral water were contaminated with benzene at ppm levels. This incident received a great deal of attention because the lethal concentration of benzene in rats is 3.8 ppm. A 250 mL sample of mineral water has 12.7 ppm of benzene. Because the contaminated mineral water is a very dilute aqueous solution, we can assume that its density is approximately 1.00 g/mL.
- What is the molarity of the solution?
- What is the mass of benzene in the sample?
Given: volume of sample, solute concentration, and density of solution
Asked for: molarity of solute and mass of solute in 250 mL
Strategy:
A Use the concentration of the solute in parts per million to calculate the molarity.
B Use the concentration of the solute in parts per million to calculate the mass of the solute in the specified volume of solution.
Solution:
-
A To calculate the molarity of benzene, we need to determine the number of moles of benzene in 1 L of solution. We know that the solution contains 12.7 ppm of benzene. Because 12.7 ppm is equivalent to 12.7 mg/1000 g of solution and the density of the solution is 1.00 g/mL, the solution contains 12.7 mg of benzene per liter (1000 mL). The molarity is therefore
-
B We are given that there are 12.7 mg of benzene per 1000 g of solution, which is equal to 12.7 mg/L of solution. Hence the mass of benzene in 250 mL (250 g) of solution is
Exercise
The maximum allowable concentration of lead in drinking water is 9.0 ppb. What is the molarity of Pb2+ in a 9.0 ppb aqueous solution? Use your calculated concentration to determine how many grams of Pb2+ are in an 8 oz glass of water.
Answer: 4.3 × 10−8 M; 2 × 10−6 g
How do chemists decide which units of concentration to use for a particular application? Although molarity is commonly used to express concentrations for reactions in solution or for titrations, it does have one drawback—molarity is the number of moles of solute divided by the volume of the solution, and the volume of a solution depends on its density, which is a function of temperature. Because volumetric glassware is calibrated at a particular temperature, typically 20°C, the molarity may differ from the original value by several percent if a solution is prepared or used at a significantly different temperature, such as 40°C or 0°C. For many applications this may not be a problem, but for precise work these errors can become important. In contrast, mole fraction, molality, and mass percentage depend on only the masses of the solute and solvent, which are independent of temperature.
Mole fraction is not very useful for experiments that involve quantitative reactions, but it is convenient for calculating the partial pressure of gases in mixtures, as we saw in Chapter 10 "Gases". As you will learn in Section 13.5 "Colligative Properties of Solutions", mole fractions are also useful for calculating the vapor pressures of certain types of solutions. Molality is particularly useful for determining how properties such as the freezing or boiling point of a solution vary with solute concentration. Because mass percentage and parts per million or billion are simply different ways of expressing the ratio of the mass of a solute to the mass of the solution, they enable us to express the concentration of a substance even when the molecular mass of the substance is unknown. Units of ppb or ppm are also used to express very low concentrations, such as those of residual impurities in foods or of pollutants in environmental studies.
Table 13.5 "Different Units for Expressing the Concentrations of Solutions*" summarizes the different units of concentration and typical applications for each. When the molar mass of the solute and the density of the solution are known, it becomes relatively easy with practice to convert among the units of concentration we have discussed, as illustrated in Example 6.
Table 13.5 Different Units for Expressing the Concentrations of Solutions*
| Unit | Definition | Application |
|---|---|---|
| molarity (M) | moles of solute/liter of solution (mol/L) | Used for quantitative reactions in solution and titrations; mass and molecular mass of solute and volume of solution are known. |
| mole fraction (X) | moles of solute/total moles present (mol/mol) | Used for partial pressures of gases and vapor pressures of some solutions; mass and molecular mass of each component are known. |
| molality (m) | moles of solute/kg of solvent (mol/kg) | Used in determining how colligative properties vary with solute concentration; masses and molecular mass of solute are known. |
| mass percentage (%) | [mass of solute (g)/mass of solution (g)] × 100 | Useful when masses are known but molecular masses are unknown. |
| parts per thousand (ppt) | [mass of solute/mass of solution] × 103 (g solute/kg solution) | Used in the health sciences, ratio solutions are typically expressed as a proportion, such as 1:1000. |
| parts per million (ppm) | [mass of solute/mass of solution] × 106 (mg solute/kg solution) | Used for trace quantities; masses are known but molecular masses may be unknown. |
| parts per billion (ppb) | [mass of solute/mass of solution] × 109 (µg solute/kg solution) | Used for trace quantities; masses are known but molecular masses may be unknown. |
| *The molarity of a solution is temperature dependent, but the other units shown in this table are independent of temperature. | ||
Example 6
Vodka is essentially a solution of pure ethanol in water. Typical vodka is sold as “80 proof,” which means that it contains 40.0% ethanol by volume. The density of pure ethanol is 0.789 g/mL at 20°C. If we assume that the volume of the solution is the sum of the volumes of the components (which is not strictly correct), calculate the following for the ethanol in 80-proof vodka.
- the mass percentage
- the mole fraction
- the molarity
- the molality
Given: volume percent and density
Asked for: mass percentage, mole fraction, molarity, and molality
Strategy:
A Use the density of the solute to calculate the mass of the solute in 100.0 mL of solution. Calculate the mass of water in 100.0 mL of solution.
B Determine the mass percentage of solute by dividing the mass of ethanol by the mass of the solution and multiplying by 100.
C Convert grams of solute and solvent to moles of solute and solvent. Calculate the mole fraction of solute by dividing the moles of solute by the total number of moles of substances present in solution.
D Calculate the molarity of the solution: moles of solute per liter of solution. Determine the molality of the solution by dividing the number of moles of solute by the kilograms of solvent.
Solution:
The key to this problem is to use the density of pure ethanol to determine the mass of ethanol (CH3CH2OH), abbreviated as EtOH, in a given volume of solution. We can then calculate the number of moles of ethanol and the concentration of ethanol in any of the required units. A Because we are given a percentage by volume, we assume that we have 100.0 mL of solution. The volume of ethanol will thus be 40.0% of 100.0 mL, or 40.0 mL of ethanol, and the volume of water will be 60.0% of 100.0 mL, or 60.0 mL of water. The mass of ethanol is obtained from its density:
If we assume the density of water is 1.00 g/mL, the mass of water is 60.0 g. We now have all the information we need to calculate the concentration of ethanol in the solution.
-
B The mass percentage of ethanol is the ratio of the mass of ethanol to the total mass of the solution, expressed as a percentage:
-
C The mole fraction of ethanol is the ratio of the number of moles of ethanol to the total number of moles of substances in the solution. Because 40.0 mL of ethanol has a mass of 31.6 g, we can use the molar mass of ethanol (46.07 g/mol) to determine the number of moles of ethanol in 40.0 mL:
Similarly, the number of moles of water is
The mole fraction of ethanol is thus
-
D The molarity of the solution is the number of moles of ethanol per liter of solution. We already know the number of moles of ethanol per 100.0 mL of solution, so the molarity is
-
The molality of the solution is the number of moles of ethanol per kilogram of solvent. Because we know the number of moles of ethanol in 60.0 g of water, the calculation is again straightforward:
Exercise
A solution is prepared by mixing 100.0 mL of toluene with 300.0 mL of benzene. The densities of toluene and benzene are 0.867 g/mL and 0.874 g/mL, respectively. Assume that the volume of the solution is the sum of the volumes of the components. Calculate the following for toluene.
- mass percentage
- mole fraction
- molarity
- molality
Answer:
- mass percentage toluene = 24.8%
- Xtoluene = 0.219
- 2.35 M toluene
- 3.59 m toluene
Summary
The concentration of a solution is the quantity of solute in a given quantity of solution. It can be expressed in several ways: molarity (moles of solute per liter of solution); mole fraction, the ratio of the number of moles of solute to the total number of moles of substances present; mass percentage, the ratio of the mass of the solute to the mass of the solution times 100; parts per thousand (ppt), grams of solute per kilogram of solution; parts per million (ppm), milligrams of solute per kilogram of solution; parts per billion (ppb), micrograms of solute per kilogram of solution; and molality (m), the number of moles of solute per kilogram of solvent.
Key Takeaway
- Different units are used to express the concentrations of a solution depending on the application.
Key Equations
molality
mass percentage
parts per million
parts per billion
Conceptual Problems
-
Does the molality have the same numerical value as the molarity for a highly concentrated aqueous solution of fructose (C6H12O6) (approximately 3.2 M)? Why or why not?
-
Explain why the molality and molarity of an aqueous solution are not always numerically identical. Will the difference between the two be greater for a dilute or a concentrated solution? Explain your answer.
-
Under what conditions are molality and molarity likely to be equal? Is the difference between the two greater when water is the solvent or when the solvent is not water? Why?
-
What is the key difference between using mole fraction or molality versus molarity to describe the concentration of a solution? Which unit(s) of concentration is most appropriate for experiments that must be carried out at several different temperatures?
-
An experiment that relies on very strict control of the reaction stoichiometry calls for adding 50.0 mL of a 0.95 M solution of A to 225 mL of a 1.01 M solution of B, followed by heating for 1 h at 60°C. To save time, a student decided to heat solution B to 60°C before measuring out 225 mL of solution B, transferring it to the flask containing solution A, and proceeding normally. This change in procedure caused the yield of product to be less than usual. How could such an apparently minor change in procedure have resulted in a decrease in the yield?
Numerical Problems
-
Complete the following table for aqueous solutions of the compounds given.
Compound Molarity (M) Solution Density (g/mL) Mole Fraction (X) H2SO4 18.0 1.84 CH3COOH 1.00 7.21 × 10−3 KOH 3.60 1.16 -
Complete the following table for each compound given.
Compound Mass (g) Volume of Solution (mL) Molarity (M) Na2SO4 7.80 225 KNO3 125 1.27 NaO2CCH3 18.64 0.95 -
How would you prepare 100.0 mL of an aqueous solution with 0.40 M KI? a solution with 0.65 M NaCN?
-
Calculate the molality of a solution with 775 mg of NaCl in 500.0 g of water. Do you expect the molarity to be the same as the molality? Why or why not?
-
What is the molarity of each solution?
- 12.8 g of glucose (C6H12O6) in water, total volume 150.0 mL
- 9.2 g of Na3PO4 in water, total volume 200.0 mL
- 843 mg of I2 in EtOH, total volume 150.0 mL
-
A medication used to treat abnormal heart rhythms is labeled “Procainamide 0.5 g/250 cc.” Express this concentration in parts per thousand.
-
Meperidine is a medication used for pain relief. A bottle of meperidine is labeled as 50 mg/mL. Express this concentration in parts per thousand.
-
An aqueous solution that is 4.61% NaOH by mass has a density of 1.06 g/mL. Calculate the molarity of the solution, the mole fraction of NaOH, and the molality of the solution.
-
A solution of concentrated phosphoric acid contains 85.0% H3PO4 by mass and has a density of 1.684 g/mL. Calculate the following.
- the molarity of the solution
- the mole fraction of H3PO4
- the molality of the solution
-
A solution of commercial concentrated nitric acid is 16 M HNO3 and has a density of 1.42 g/mL. What is the percentage of HNO3 in the solution by mass? What is the molality?
-
A commercial aqueous ammonia solution contains 28.0% NH3 by massand has a density of 0.899 g/mL. Calculate the following.
- the molarity
- the mole fraction
-
Concentrated, or glacial, acetic acid is pure acetic acid and has a density of 1.053 g/mL. It is widely used in organic syntheses, in the manufacture of rayon and plastics, as a preservative in foods, and occasionally to treat warts. What volume of glacial acetic acid is required to prepare 5.00 L of a 1.75 M solution of acetic acid in ethanol?
-
Solutions of sodium carbonate decahydrate, also known as washing soda, are used as skin cleansers. The solubility of this compound in cold water is 21.52 g/100 mL. If a saturated solution has a density of 1.20 g/mL, what is its molarity? What is the mole fraction of sodium carbonate decahydrate in this solution?
-
Hydrogen peroxide (H2O2) is usually sold over the counter as an aqueous solution that is 3% by mass. Assuming a solution density of 1.01 g/mL, what is the molarity of hydrogen peroxide? What is the molar concentration of a solution that is 30% hydrogen peroxide by mass (density = 1.112 g/mL)? How would you prepare 100.0 mL of a 3% solution from the 30% solution?
-
Determine the concentration of a solution with 825 mg of Na2HPO4 dissolved in 450.0 mL of H2O at 20°C in molarity, molality, mole fraction, and parts per million. Assume that the density of the solution is the same as that of water. Which unit of concentration is most convenient for calculating vapor pressure changes? Why?
-
How many moles of Cl− are there in 25.0 mL of a 0.15 M CaCl2 solution?
-
How many moles of Na+ are there in 25.0 g of a 1.33 × 10−3 m Na2HPO4 solution? What is the sodium concentration of this solution in ppb?
-
How many grams of copper are there in 30.0 mL of a 0.100 M CuSO4 solution?
-
How many grams of nitrate ion are there in 75.0 g of a 1.75 × 10−4 m Pb(NO3)2 solution? What is the nitrate concentration of the solution in ppb?
-
How many milliliters of a 0.750 M solution of K2CrO4 are required to deliver 250 mg of chromate ion?
-
How many milliliters of a 1.95 × 10−6 M solution of Ag3PO4 are required to deliver 14.0 mg of Ag+?
-
Iron reacts with bromine according to the following equation:
2Fe(s) + 3Br2(aq) → 2FeBr3(aq)How many milliliters of a 5.0 × 10−2 M solution of bromine in water are required to react completely with 750.0 mg of iron metal?
-
Aluminum reacts with HCl according to the following equation:
2Al(s) + 6HCl(aq) → 2AlCl3(aq) + 3H2(g)If 25.0 mL of a solution of HCl in water is required to react completely with 1.05 g of aluminum metal, what is the molarity of the HCl solution?
-
The precipitation of silver chloride is a diagnostic test for the presence of chloride ion. If 25.0 mL of 0.175 M AgNO3 are required to completely precipitate the chloride ions from 10.0 mL of an NaCl solution, what was the original concentration of NaCl?
-
Barium sulfate is virtually insoluble. If a 10.0 mL solution of 0.333 M Ba(NO3)2 is stirred with 40.0 mL of a 0.100 M Na2SO4, how many grams of barium sulfate will precipitate? Which reactant is present in excess? What is its final concentration?
Answers
-
Compound Molarity (M) Solution Density (g/mL) Mole Fraction (X) H2SO4 18.0 1.84 0.82 CH3COOH 0.393 1.00 7.21 × 10−3 KOH 3.60 1.16 6.33 × 10 −2 -
-
100.0 ml of 0.40 M KI: dissolve 6.64 g of KI in enough water to make 100.0 mL of solution; 100.0 ml of 0.65 M NaCN: dissolve 3.18 g of NaCN in enough water to make 100.0 mL of solution.
-
-
- 0.474 M glucose
- 0.28 M Na3PO4
- 0.0221 M I2
-
-
-
-
- 14.6 M
- X = 0.510
- 57.7 m
-
-
- 14.8 M
- X = 0.292
-
-
The molarity is 0.745 M, and the mole fraction is 0.0134.
-
-
The molarity is 0.0129 M, the molality is 0.0129 m, the mole fraction is 2.33 × 10−4, and the solution contains 1830 ppm Na2HPO4. Mole fraction is most useful for calculating vapor pressure, because Raoult’s law states that the vapor pressure of a solution containing a non-volatile solute is equal to the mole fraction of solvent times the vapor pressure of the pure solvent. The mole fraction of the solvent is just one minus the mole fraction of solute.
-
-
6.65 × 10−5 mol sodium; 6.14 × 104 ppb
-
-
1.63 × 10−3 g; 2.17 × 104 ppb
-
-
2.22 × 104 mL or 22.2 L
-
-
4.68 M HCl
-
-
0.777 g BaSO4; Na2SO4; 0.0134 M Na2SO4
13.4 Effects of Temperature and Pressure on Solubility
Learning Objective
- To understand the relationship among temperature, pressure, and solubility.
Experimentally it is found that the solubility of most compounds depends strongly on temperature and, if a gas, on pressure as well. As we shall see, the ability to manipulate the solubility by changing the temperature and pressure has several important consequences.
Effect of Temperature on the Solubility of Solids
Figure 13.9 "Solubilities of Several Inorganic and Organic Solids in Water as a Function of Temperature" shows plots of the solubilities of several organic and inorganic compounds in water as a function of temperature. Although the solubility of a solid generally increases with increasing temperature, there is no simple relationship between the structure of a substance and the temperature dependence of its solubility. Many compounds (such as glucose and CH3CO2Na) exhibit a dramatic increase in solubility with increasing temperature. Others (such as NaCl and K2SO4) exhibit little variation, and still others (such as Li2SO4) become less soluble with increasing temperature.
Figure 13.9 Solubilities of Several Inorganic and Organic Solids in Water as a Function of Temperature
Solubility may increase or decrease with temperature; the magnitude of this temperature dependence varies widely among compounds.
Notice in particular the curves for NH4NO3 and CaCl2. The dissolution of ammonium nitrate in water is endothermic (ΔHsoln = +25.7 kJ/mol), whereas the dissolution of calcium chloride is exothermic (ΔHsoln = −68.2 kJ/mol), yet Figure 13.9 "Solubilities of Several Inorganic and Organic Solids in Water as a Function of Temperature" shows that the solubility of both compounds increases sharply with increasing temperature. In fact, the magnitudes of the changes in both enthalpy and entropy for dissolution are temperature dependent. Because the solubility of a compound is ultimately determined by relatively small differences between large numbers, there is generally no good way to predict how the solubility will vary with temperature.
The variation of solubility with temperature has been measured for a wide range of compounds, and the results are published in many standard reference books. Chemists are often able to use this information to separate the components of a mixture by fractional crystallizationThe separation of compounds based on their relative solubilities in a given solvent., the separation of compounds on the basis of their solubilities in a given solvent. For example, if we have a mixture of 150 g of sodium acetate (CH3CO2Na) and 50 g of KBr, we can separate the two compounds by dissolving the mixture in 100 g of water at 80°C and then cooling the solution slowly to 0°C. According to the temperature curves in Figure 13.9 "Solubilities of Several Inorganic and Organic Solids in Water as a Function of Temperature", both compounds dissolve in water at 80°C, and all 50 g of KBr remains in solution at 0°C. Only about 36 g of CH3CO2Na are soluble in 100 g of water at 0°C, however, so approximately 114 g (150 g − 36 g) of CH3CO2Na crystallizes out on cooling. The crystals can then be separated by filtration. Thus fractional crystallization allows us to recover about 75% of the original CH3CO2Na in essentially pure form in only one step.
Fractional crystallization is a common technique for purifying compounds as diverse as those shown in Figure 13.9 "Solubilities of Several Inorganic and Organic Solids in Water as a Function of Temperature" and from antibiotics to enzymes. For the technique to work properly, the compound of interest must be more soluble at high temperature than at low temperature, so that lowering the temperature causes it to crystallize out of solution. In addition, the impurities must be more soluble than the compound of interest (as was KBr in this example) and preferably present in relatively small amounts.
Effect of Temperature on the Solubility of Gases
The solubility of gases in liquids decreases with increasing temperature, as shown in Figure 13.10 "Solubilities of Several Common Gases in Water as a Function of Temperature at Partial Pressure of 1 atm". Attractive intermolecular interactions in the gas phase are essentially zero for most substances. When a gas dissolves, it does so because its molecules interact with solvent molecules. Because heat is released when these new attractive interactions form, dissolving most gases in liquids is an exothermic process (ΔHsoln < 0). Conversely, adding heat to the solution provides thermal energy that overcomes the attractive forces between the gas and the solvent molecules, thereby decreasing the solubility of the gas.The phenomenon is similar to that involved in the increase in vapor pressure of a pure liquid with increasing temperature, as discussed in Chapter 11 "Liquids". In the case of vapor pressure, however, it is attractive forces between solvent molecules that are being overcome by the added thermal energy when the temperature is increased.
Figure 13.10 Solubilities of Several Common Gases in Water as a Function of Temperature at Partial Pressure of 1 atm
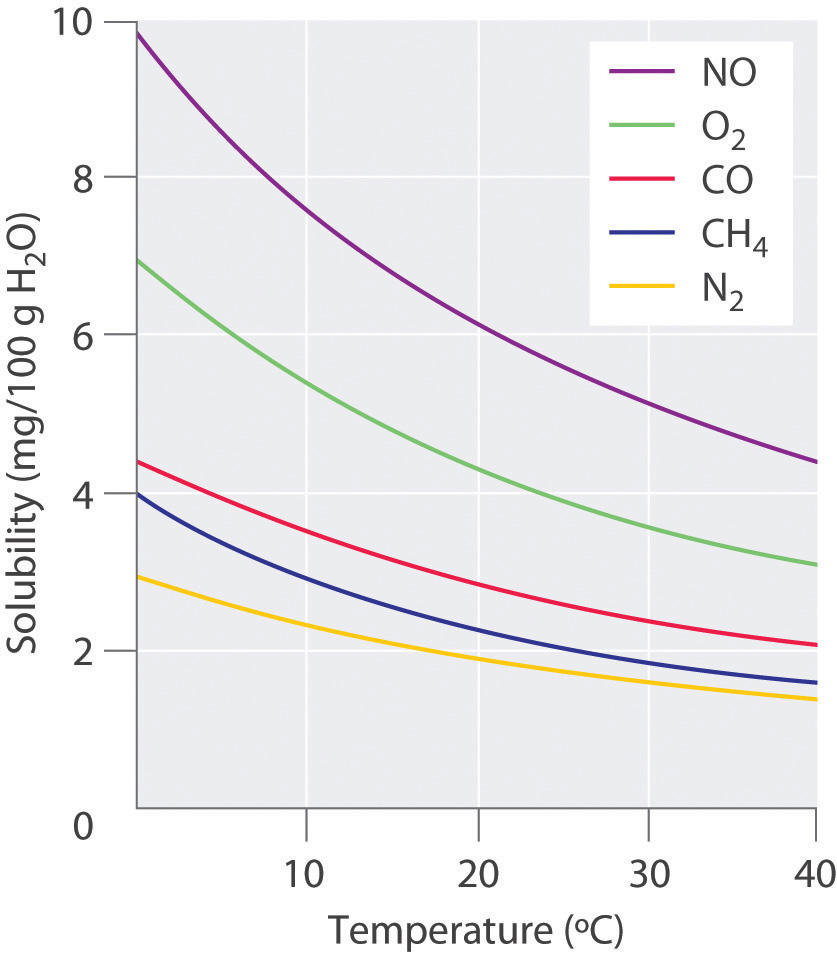
The solubilities of all gases decrease with increasing temperature.
The decrease in the solubilities of gases at higher temperatures has both practical and environmental implications. Anyone who routinely boils water in a teapot or electric kettle knows that a white or gray deposit builds up on the inside and must eventually be removed. The same phenomenon occurs on a much larger scale in the giant boilers used to supply hot water or steam for industrial applications, where it is called “boiler scale,” a deposit that can seriously decrease the capacity of hot water pipes (Figure 13.11 "Boiler Scale in a Water Pipe"). The problem is not a uniquely modern one: aqueducts that were built by the Romans 2000 years ago to carry cold water from alpine regions to warmer, drier regions in southern France were clogged by similar deposits. The chemistry behind the formation of these deposits is moderately complex and will be described in more detail in Chapter 17 "Solubility and Complexation Equilibriums", but the driving force is the loss of dissolved CO2 from solution. Hard water contains dissolved Ca2+ and HCO3− (bicarbonate) ions. Calcium bicarbonate [Ca(HCO3)2] is rather soluble in water, but calcium carbonate (CaCO3) is quite insoluble. A solution of bicarbonate ions can react to form carbon dioxide, carbonate ion, and water:
Equation 13.9
2HCO3−(aq) → CO22−(aq) + H2O(l) + CO2(aq)Heating the solution decreases the solubility of CO2, which escapes into the gas phase above the solution. In the presence of calcium ions, the carbonate ions precipitate as insoluble calcium carbonate, the major component of boiler scale.
Figure 13.11 Boiler Scale in a Water Pipe

Calcium carbonate (CaCO3) deposits in hot water pipes can significantly reduce pipe capacity. These deposits, called boiler scale, form when dissolved CO2 is driven into the gas phase at high temperatures.
In thermal pollution, lake or river water that is used to cool an industrial reactor or a power plant is returned to the environment at a higher temperature than normal. Because of the reduced solubility of O2 at higher temperatures (Figure 13.10 "Solubilities of Several Common Gases in Water as a Function of Temperature at Partial Pressure of 1 atm"), the warmer water contains less dissolved oxygen than the water did when it entered the plant. Fish and other aquatic organisms that need dissolved oxygen to live can literally suffocate if the oxygen concentration of their habitat is too low. Because the warm, oxygen-depleted water is less dense, it tends to float on top of the cooler, denser, more oxygen-rich water in the lake or river, forming a barrier that prevents atmospheric oxygen from dissolving. Eventually even deep lakes can be suffocated if the problem is not corrected. Additionally, most fish and other nonmammalian aquatic organisms are cold-blooded, which means that their body temperature is the same as the temperature of their environment. Temperatures substantially greater than the normal range can lead to severe stress or even death. Cooling systems for power plants and other facilities must be designed to minimize any adverse effects on the temperatures of surrounding bodies of water.
A similar effect is seen in the rising temperatures of bodies of water such as the Chesapeake Bay, the largest estuary in North America, where global warming has been implicated as the cause (For more information on global warming, see Chapter 5 "Energy Changes in Chemical Reactions", Section 5.5 "Energy Sources and the Environment".) For each 1.5°C that the bay’s water warms, the capacity of water to dissolve oxygen decreases by about 1.1%. Many marine species that are at the southern limit of their distributions have shifted their populations farther north. In 2005, the eelgrass, which forms an important nursery habitat for fish and shellfish, disappeared from much of the bay following record high water temperatures. Presumably, decreased oxygen levels decreased populations of clams and other filter feeders, which then decreased light transmission to allow the eelsgrass to grow. The complex relationships in ecosystems such as the Chesapeake Bay are especially sensitive to temperature fluctuations that cause a deterioration of habitat quality.
Effect of Pressure on the Solubility of Gases: Henry’s Law
External pressure has very little effect on the solubility of liquids and solids. In contrast, the solubility of gases increases as the partial pressure of the gas above a solution increases. This point is illustrated in Figure 13.12 "A Model Depicting Why the Solubility of a Gas Increases as the Partial Pressure Increases at Constant Temperature", which shows the effect of increased pressure on the dynamic equilibrium that is established between the dissolved gas molecules in solution and the molecules in the gas phase above the solution. Because the concentration of molecules in the gas phase increases with increasing pressure, the concentration of dissolved gas molecules in the solution at equilibrium is also higher at higher pressures.
Figure 13.12 A Model Depicting Why the Solubility of a Gas Increases as the Partial Pressure Increases at Constant Temperature
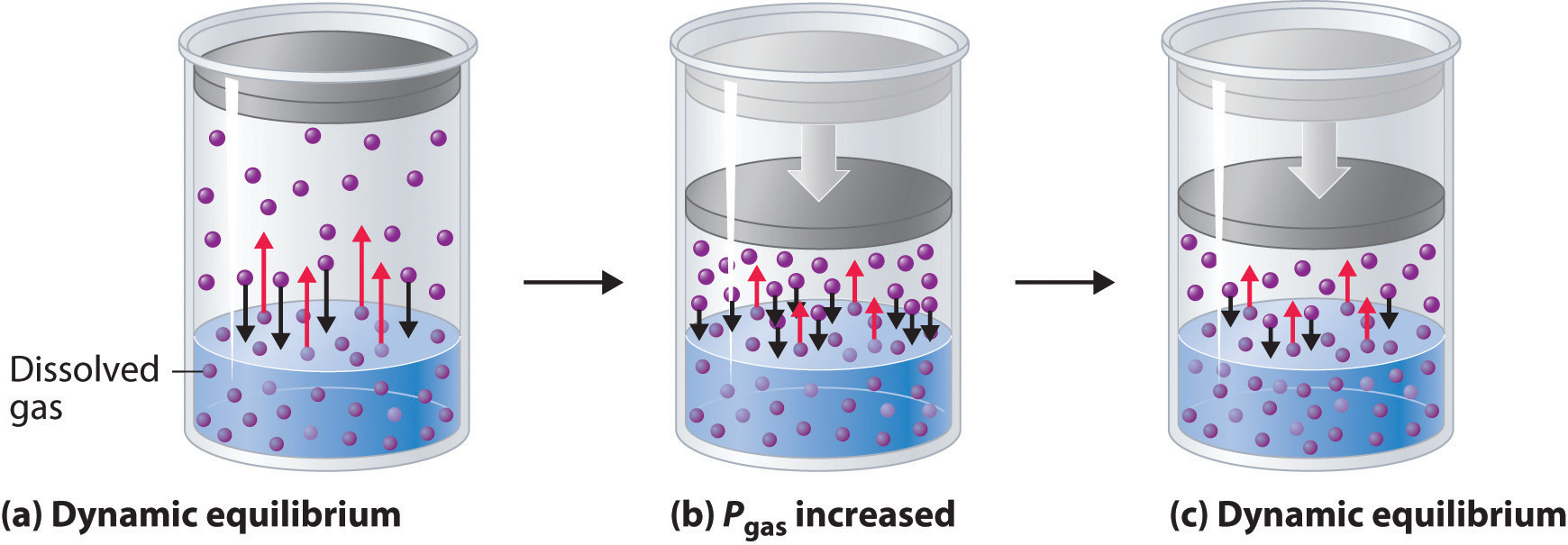
(a) When a gas comes in contact with a pure liquid, some of the gas molecules (purple spheres) collide with the surface of the liquid and dissolve. When the concentration of dissolved gas molecules has increased so that the rate at which gas molecules escape into the gas phase is the same as the rate at which they dissolve, a dynamic equilibrium has been established, as depicted here. This equilibrium is entirely analogous to the one that maintains the vapor pressure of a liquid. (For more information on vapor pressure, see Chapter 11 "Liquids", Section 11.3 "Unique Properties of Liquids".) (b) Increasing the pressure of the gas increases the number of molecules of gas per unit volume, which increases the rate at which gas molecules collide with the surface of the liquid and dissolve. (c) As additional gas molecules dissolve at the higher pressure, the concentration of dissolved gas increases until a new dynamic equilibrium is established.
The relationship between pressure and the solubility of a gas is described quantitatively by Henry’s lawAn equation that quantifies the relationship between the pressure and the solubility of a gas: , which is named for its discoverer, the English physician and chemist, William Henry (1775–1836):
Equation 13.10
C = kPwhere C is the concentration of dissolved gas at equilibrium, P is the partial pressure of the gas, and k is the Henry’s law constant, which must be determined experimentally for each combination of gas, solvent, and temperature. Although the gas concentration may be expressed in any convenient units, we will use molarity exclusively. The units of the Henry’s law constant are therefore mol/(L·atm) = M/atm. Values of the Henry’s law constants for solutions of several gases in water at 20°C are listed in Table 13.6 "Henry’s Law Constants for Selected Gases in Water at 20°C".
As the data in Table 13.6 "Henry’s Law Constants for Selected Gases in Water at 20°C" demonstrate, the concentration of a dissolved gas in water at a given pressure depends strongly on its physical properties. For a series of related substances, London dispersion forces increase as molecular mass increases. Thus among the elements of group 18, the Henry’s law constants increase smoothly from He to Ne to Ar. The table also shows that O2 is almost twice as soluble as N2. Although London dispersion forces are too weak to explain such a large difference, O2 is paramagnetic and hence more polarizable than N2, which explains its high solubility.
Table 13.6 Henry’s Law Constants for Selected Gases in Water at 20°C
| Gas | Henry’s Law Constant [mol/(L·atm)] × 10−4 |
|---|---|
| He | 3.9 |
| Ne | 4.7 |
| Ar | 15 |
| H2 | 8.1 |
| N2 | 7.1 |
| O2 | 14 |
| CO2 | 392 |
Gases that react chemically with water, such as HCl and the other hydrogen halides, H2S, and NH3, do not obey Henry’s law; all of these gases are much more soluble than predicted by Henry’s law. For example, HCl reacts with water to give H+(aq) and Cl−(aq), not dissolved HCl molecules, and its dissociation into ions results in a much higher solubility than expected for a neutral molecule.
Note the Pattern
Gases that react with water do not obey Henry’s law.
Henry’s law has important applications. For example, bubbles of CO2 form as soon as a carbonated beverage is opened because the drink was bottled under CO2 at a pressure greater than 1 atm. When the bottle is opened, the pressure of CO2 above the solution drops rapidly, and some of the dissolved gas escapes from the solution as bubbles. Henry’s law also explains why scuba divers have to be careful to ascend to the surface slowly after a dive if they are breathing compressed air. At the higher pressures under water, more N2 from the air dissolves in the diver’s internal fluids. If the diver ascends too quickly, the rapid pressure change causes small bubbles of N2 to form throughout the body, a condition known as “the bends.” These bubbles can block the flow of blood through the small blood vessels, causing great pain and even proving fatal in some cases.
Due to the low Henry’s law constant for O2 in water, the levels of dissolved oxygen in water are too low to support the energy needs of multicellular organisms, including humans. To increase the O2 concentration in internal fluids, organisms synthesize highly soluble carrier molecules that bind O2 reversibly. For example, human red blood cells contain a protein called hemoglobin that specifically binds O2 and facilitates its transport from the lungs to the tissues, where it is used to oxidize food molecules to provide energy. The concentration of hemoglobin in normal blood is about 2.2 mM, and each hemoglobin molecule can bind four O2 molecules. Although the concentration of dissolved O2 in blood serum at 37°C (normal body temperature) is only 0.010 mM, the total dissolved O2 concentration is 8.8 mM, almost a thousand times greater than would be possible without hemoglobin. Synthetic oxygen carriers based on fluorinated alkanes have been developed for use as an emergency replacement for whole blood. Unlike donated blood, these “blood substitutes” do not require refrigeration and have a long shelf life. Their very high Henry’s law constants for O2 result in dissolved oxygen concentrations comparable to those in normal blood.
Example 7
The Henry’s law constant for O2 in water at 25°C is 1.27 × 10−3 M/atm, and the mole fraction of O2 in the atmosphere is 0.21. Calculate the solubility of O2 in water at 25°C at an atmospheric pressure of 1.00 atm.
Given: Henry’s law constant, mole fraction of O2, and pressure
Asked for: solubility
Strategy:
A Use Dalton’s law of partial pressures to calculate the partial pressure of oxygen. (For more information about Dalton’s law of partial pressures, see Chapter 10 "Gases", Section 10.5 "Mixtures of Gases".)
B Use Henry’s law to calculate the solubility, expressed as the concentration of dissolved gas.
Solution:
A According to Dalton’s law, the partial pressure of O2 is proportional to the mole fraction of O2:
PA = XAPt = (0.21)(1.00 atm) = 0.21 atmB From Henry’s law, the concentration of dissolved oxygen under these conditions is
Exercise
To understand why soft drinks “fizz” and then go “flat” after being opened, calculate the concentration of dissolved CO2 in a soft drink
- bottled under a pressure of 5.0 atm of CO2.
- in equilibrium with the normal partial pressure of CO2 in the atmosphere (approximately 3 × 10−4 atm).
The Henry’s law constant for CO2 in water at 25°C is 3.4 × 10−2 M/atm.
Answer:
- 0.17 M
- 1 × 10−5 M
Summary
The solubility of most substances depends strongly on the temperature and, in the case of gases, on the pressure. The solubility of most solid or liquid solutes increases with increasing temperature. The components of a mixture can often be separated using fractional crystallization, which separates compounds according to their solubilities. The solubility of a gas decreases with increasing temperature. Henry’s law describes the relationship between the pressure and the solubility of a gas.
Key Takeaway
- The solubility of a solid may increase or decrease with increasing temperature, whereas the solubility of a gas decreases with an increase in temperature and a decrease in pressure.
Conceptual Problems
-
Use the kinetic molecular theory of gases discussed in Chapter 10 "Gases" to explain why the solubility of virtually all gases in liquids decreases with increasing temperature.
-
An industrial plant uses water from a nearby stream to cool its reactor and returns the water to the stream after use. Over a period of time, dead fish start to appear downstream from the plant, but there is no evidence for any leaks of potentially toxic chemicals into the stream. What other factor might be causing the fish to die?
-
One manufacturer’s instructions for setting up an aquarium specify that if boiled water is used, the water must be cooled to room temperature and allowed to stand overnight before fish are added. Why is it necessary for the water to stand?
-
Using a carbonated beverage as an example, discuss the effect of temperature on the “fizz.” How does the “foaminess” of a carbonated beverage differ between Los Angeles, California, and Denver, Colorado?
-
A common laboratory technique for degassing a solvent is to place it in a flask that is sealed to the atmosphere and then evacuate the flask to remove any gases above the liquid. Why is this procedure effective? Why does the temperature of the solvent usually decrease substantially during this process?
Answers
-
-
-
When water is boiled, all of the dissolved oxygen and nitrogen are removed. When the water is cooled to room temperature, it initially contains very little dissolved oxygen. Allowing the water to stand overnight allows oxygen in the air to dissolve, so that the fish will not suffocate.
-
-
Evacuating the flask to remove gases decreases the partial pressure of oxygen above the solution. According to Henry’s law, the solubility of any gas decreases as its partial pressure above the solution decreases. Consequently, dissolved oxygen escapes from solution into the gas phase, where it is removed by the vacuum pump. Filling the flask with nitrogen gas and repeating this process several times effectively removes almost all of the dissolved oxygen. The temperature of the solvent decreases because some solvent evaporates as well during this process. The heat that is required to evaporate some of the liquid is initially removed from the rest of the solvent, decreasing its temperature.
Numerical Problems
-
The solubility of CO2 in water at 0°C and 1 atm is 0.335 g/100 g of H2O. At 20°C and 1 atm, the solubility of CO2 in water is 0.169 g/100 g of H2O.
- What volume of CO2 would be released by warming 750 g of water saturated with CO2 from 0°C to 20°C?
- What is the value of the Henry’s law constant for CO2 under each set of conditions?
-
The solubility of O2 in 100 g of H2O at varying temperatures and a pressure of 1 atm is given in the following table:
Solubility (g) Temperature (°C) 0.0069 0 0.0054 10 0.0043 20 - What is the value of the Henry’s law constant at each temperature?
- Does Henry’s law constant increase or decrease with increasing temperature?
- At what partial pressure of O2 would the concentration of O2 in water at 0°C be the same as the concentration in water at 20°C at a partial pressure of 1 atm?
- Assuming that air is 20% O2 by volume, at what atmospheric pressure would the O2 concentration be the same at 20°C as it is at atmospheric pressure and 0°C?
Answer
-
- 0.678 L CO2
- k0°C = 7.61 × 10−2 M/atm, k20°C = 3.84 × 10−2 M/atm
-
13.5 Colligative Properties of Solutions
Learning Objective
- To describe the relationship between solute concentration and the physical properties of a solution.
Many of the physical properties of solutions differ significantly from those of the pure substances discussed in earlier chapters, and these differences have important consequences. For example, the limited temperature range of liquid water (0°C–100°C) severely limits its use. Aqueous solutions have both a lower freezing point and a higher boiling point than pure water. Probably one of the most familiar applications of this phenomenon is the addition of ethylene glycol (“antifreeze”) to the water in an automobile radiator. This solute lowers the freezing point of the water, preventing the engine from cracking in very cold weather from the expansion of pure water on freezing. Antifreeze also enables the cooling system to operate at temperatures greater than 100°C without generating enough pressure to explode.
Changes in the freezing point and boiling point of a solution depend primarily on the number of solute particles present rather than the kind of particles. Such properties of solutions are called colligative propertiesA property of a solution that depends primarily on the number of solute particles rather than the kind of solute particles. (from the Latin colligatus, meaning “bound together” as in a quantity). As we will see, the vapor pressure and osmotic pressure of solutions are also colligative properties.
When we determine the number of particles in a solution, it is important to remember that not all solutions with the same molarity contain the same concentration of solute particles. Consider, for example, 0.01 M aqueous solutions of sucrose, NaCl, and CaCl2. Because sucrose dissolves to give a solution of neutral molecules, the concentration of solute particles in a 0.01 M sucrose solution is 0.01 M. In contrast, both NaCl and CaCl2 are ionic compounds that dissociate in water to yield solvated ions. As a result, a 0.01 M aqueous solution of NaCl contains 0.01 M Na+ ions and 0.01 M Cl− ions, for a total particle concentration of 0.02 M. Similarly, the CaCl2 solution contains 0.01 M Ca2+ ions and 0.02 M Cl− ions, for a total particle concentration of 0.03 M.These values are correct for dilute solutions, where the dissociation of the compounds to form separately solvated ions is complete. At higher concentrations (typically >1 M), especially with salts of small, highly charged ions (such as Mg2+ or Al3+), or in solutions with less polar solvents, dissociation to give separate ions is often incomplete (see Figure 13.21 "Ion Pairs"). The sum of the concentrations of the dissolved solute particles dictates the physical properties of a solution. In the following discussion, we must therefore keep the chemical nature of the solute firmly in mind.
Vapor Pressure of Solutions and Raoult’s Law
Adding a nonvolatile solute, one whose vapor pressure is too low to measure readily, to a volatile solvent decreases the vapor pressure of the solvent. We can understand this phenomenon qualitatively by examining Figure 13.13 "A Model Depicting Why the Vapor Pressure of a Solution of Glucose Is Less Than the Vapor Pressure of Pure Water", which is a schematic diagram of the surface of a solution of glucose in water. In an aqueous solution of glucose, a portion of the surface area is occupied by nonvolatile glucose molecules rather than by volatile water molecules. As a result, fewer water molecules can enter the vapor phase per unit time, even though the surface water molecules have the same kinetic energy distribution as they would in pure water. At the same time, the rate at which water molecules in the vapor phase collide with the surface and reenter the solution is unaffected. The net effect is to shift the dynamic equilibrium between water in the vapor and the liquid phases, decreasing the vapor pressure of the solution compared with the vapor pressure of the pure solvent.
Figure 13.13 A Model Depicting Why the Vapor Pressure of a Solution of Glucose Is Less Than the Vapor Pressure of Pure Water
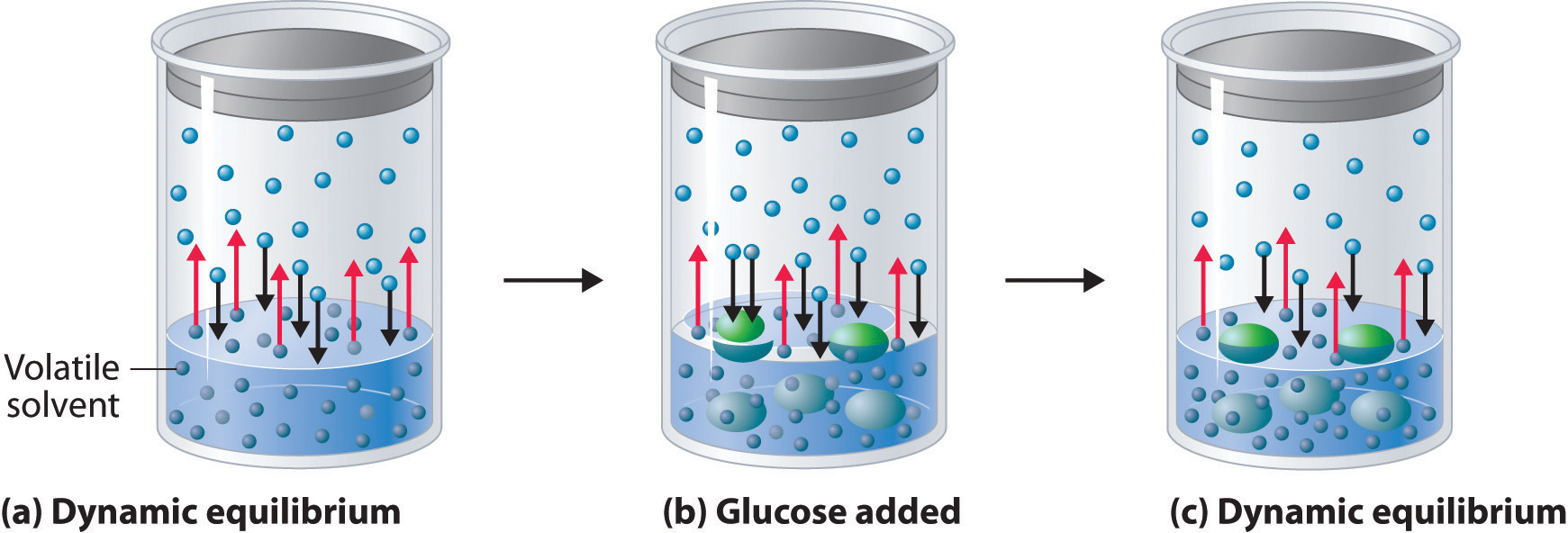
(a) When water or any volatile solvent is in a closed container, water molecules move into and out of the liquid phase at the same rate in a dynamic equilibrium. (b) If a nonvolatile solute such as glucose is added, some fraction of the surface area is occupied by solvated solute molecules. As a result, the rate at which water molecules evaporate is decreased, although initially their rate of condensation is unchanged. (c) When the glucose solution reaches equilibrium, the concentration of water molecules in the vapor phase, and hence the vapor pressure, is less than that of pure water.
Figure 13.14 "Transfer of Water to a Beaker Containing a Glucose Solution" shows two beakers, one containing pure water and one containing an aqueous glucose solution, in a sealed chamber. We can view the system as having two competing equilibria: water vapor will condense in both beakers at the same rate, but water molecules will evaporate more slowly from the glucose solution because fewer water molecules are at the surface. Eventually all of the water will evaporate from the beaker containing the liquid with the higher vapor pressure (pure water) and condense in the beaker containing the liquid with the lower vapor pressure (the glucose solution). If the system consisted of only a beaker of water inside a sealed container, equilibrium between the liquid and vapor would be achieved rather rapidly, and the amount of liquid water in the beaker would remain constant.
Figure 13.14 Transfer of Water to a Beaker Containing a Glucose Solution
(top) One beaker contains an aqueous solution of glucose, and the other contains pure water. If they are placed in a sealed chamber, the lower vapor pressure of water in the glucose solution results in a net transfer of water from the beaker containing pure water to the beaker containing the glucose solution. (bottom) Eventually, all of the water is transferred to the beaker that has the glucose solution.
If the particles of a solute are essentially the same size as those of the solvent and both solute and solvent have roughly equal probabilities of being at the surface of the solution, then the effect of a solute on the vapor pressure of the solvent is proportional to the number of sites occupied by solute particles at the surface of the solution. Doubling the concentration of a given solute causes twice as many surface sites to be occupied by solute molecules, resulting in twice the decrease in vapor pressure. The relationship between solution composition and vapor pressure is therefore
Equation 13.11
where PA is the vapor pressure of component A of the solution (in this case the solvent), XA is the mole fraction of A in solution, and is the vapor pressure of pure A. Equation 13.11 is known as Raoult’s lawAn equation that quantifies the relationship between solution composition and vapor pressure: , after the French chemist who developed it. If the solution contains only a single nonvolatile solute (B), then XA + XB = 1, and we can substitute XA = 1 − XB to obtain
Equation 13.12
Rearranging and defining we obtain a relationship between the decrease in vapor pressure and the mole fraction of nonvolatile solute:
Equation 13.13
We can solve vapor pressure problems in either of two ways: by using Equation 13.11 to calculate the actual vapor pressure above a solution of a nonvolatile solute, or by using Equation 13.13 to calculate the decrease in vapor pressure caused by a specified amount of a nonvolatile solute.
Example 8
Ethylene glycol (HOCH2CH2OH), the major ingredient in commercial automotive antifreeze, increases the boiling point of radiator fluid by lowering its vapor pressure. At 100°C, the vapor pressure of pure water is 760 mmHg. Calculate the vapor pressure of an aqueous solution containing 30.2% ethylene glycol by mass, a concentration commonly used in climates that do not get extremely cold in winter.
Given: identity of solute, percentage by mass, and vapor pressure of pure solvent
Asked for: vapor pressure of solution
Strategy:
A Calculate the number of moles of ethylene glycol in an arbitrary quantity of water, and then calculate the mole fraction of water.
B Use Raoult’s law to calculate the vapor pressure of the solution.
Solution:
A A 30.2% solution of ethylene glycol contains 302 g of ethylene glycol per kilogram of solution; the remainder (698 g) is water. To use Raoult’s law to calculate the vapor pressure of the solution, we must know the mole fraction of water. Thus we must first calculate the number of moles of both ethylene glycol (EG) and water present:
The mole fraction of water is thus
B From Raoult’s law (Equation 13.11), the vapor pressure of the solution is
Alternatively, we could solve this problem by calculating the mole fraction of ethylene glycol and then using Equation 13.13 to calculate the resulting decrease in vapor pressure:
The same result is obtained using either method.
Exercise
Seawater is an approximately 3.0% aqueous solution of NaCl by mass with about 0.5% of other salts by mass. Calculate the decrease in the vapor pressure of water at 25°C caused by this concentration of NaCl, remembering that 1 mol of NaCl produces 2 mol of solute particles. The vapor pressure of pure water at 25°C is 23.8 mmHg.
Answer: 0.45 mmHg. This may seem like a small amount, but it constitutes about a 2% decrease in the vapor pressure of water and accounts in part for the higher humidity in the north-central United States near the Great Lakes, which are freshwater lakes. The decrease therefore has important implications for climate modeling.
Even when a solute is volatile, meaning that it has a measurable vapor pressure, we can still use Raoult’s law. In this case, we calculate the vapor pressure of each component separately. The total vapor pressure of the solution (PT) is the sum of the vapor pressures of the components:
Equation 13.14
Because XB = 1 − XA for a two-component system,
Equation 13.15
Thus we need to specify the mole fraction of only one of the components in a two-component system. Consider, for example, the vapor pressure of solutions of benzene and toluene of various compositions. At 20°C, the vapor pressures of pure benzene and toluene are 74.7 and 22.3 mmHg, respectively. The vapor pressure of benzene in a benzene–toluene solution is
Equation 13.16
and the vapor pressure of toluene in the solution is
Equation 13.17
Equation 13.16 and Equation 13.17 are both in the form of the equation for a straight line: y = mx + b, where b = 0. Plots of the vapor pressures of both components versus the mole fractions are therefore straight lines that pass through the origin, as shown in Figure 13.15 "Vapor Pressures of Benzene–Toluene Solutions". Furthermore, a plot of the total vapor pressure of the solution versus the mole fraction is a straight line that represents the sum of the vapor pressures of the pure components. Thus the vapor pressure of the solution is always greater than the vapor pressure of either component.
Figure 13.15 Vapor Pressures of Benzene–Toluene Solutions
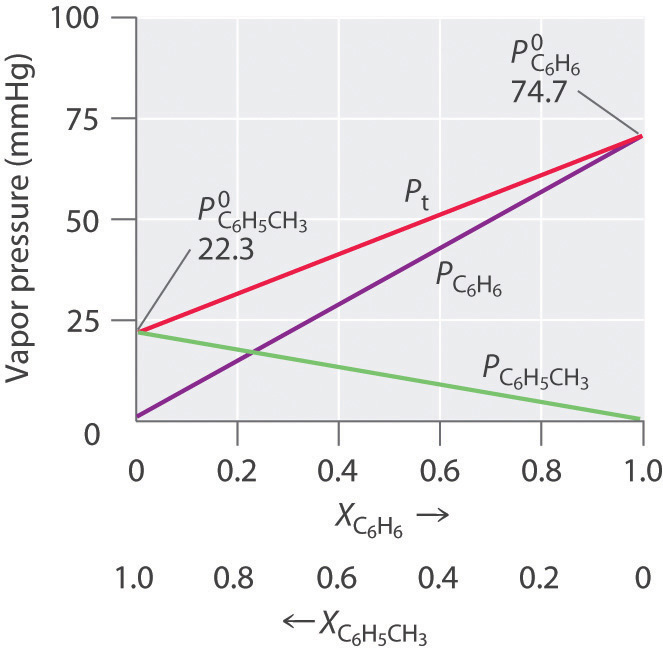
Plots of the vapor pressures of benzene (C6H6) and toluene (C6H5CH3) versus the mole fractions at 20°C are straight lines. For a solution like this, which approximates an ideal solution, the total vapor pressure of the solution (Pt) is the sum of the vapor pressures of the components.
A solution of two volatile components that behaves like the solution in Figure 13.15 "Vapor Pressures of Benzene–Toluene Solutions" is an ideal solutionA solution that obeys Raoult’s law., which is defined as a solution that obeys Raoult’s law. Like an ideal gas, an ideal solution is a hypothetical system whose properties can be described in terms of a simple model. Mixtures of benzene and toluene approximate an ideal solution because the intermolecular forces in the two pure liquids are almost identical in both kind and magnitude. Consequently, the change in enthalpy on solution formation is essentially zero (ΔHsoln ≈ 0), which is one of the defining characteristics of an ideal solution.
Note the Pattern
Ideal solutions and ideal gases are both simple models that ignore intermolecular interactions.
Most real solutions, however, do not obey Raoult’s law precisely, just as most real gases do not obey the ideal gas law exactly. Real solutions generally deviate from Raoult’s law because the intermolecular interactions between the two components A and B differ. We can distinguish between two general kinds of behavior, depending on whether the intermolecular interactions between molecules A and B are stronger or weaker than the A–A and B–B interactions in the pure components. If the A–B interactions are stronger than the A–A and B–B interactions, each component of the solution exhibits a lower vapor pressure than expected for an ideal solution, as does the solution as a whole. The favorable A–B interactions effectively stabilize the solution compared with the vapor. This kind of behavior is called a negative deviation from Raoult’s law. Systems stabilized by hydrogen bonding between two molecules, such as acetone and ethanol, exhibit negative deviations from Raoult’s law. Conversely, if the A–B interactions are weaker than the A–A and B–B interactions yet the entropy increase is enough to allow the solution to form, both A and B have an increased tendency to escape from the solution into the vapor phase. The result is a higher vapor pressure than expected for an ideal solution, producing a positive deviation from Raoult’s law. In a solution of CCl4 and methanol, for example, the nonpolar CCl4 molecules interrupt the extensive hydrogen bonding network in methanol, and the lighter methanol molecules have weaker London dispersion forces than the heavier CCl4 molecules. Consequently, solutions of CCl4 and methanol exhibit positive deviations from Raoult’s law.
Example 9
For each system, compare the intermolecular interactions in the pure liquids and in the solution to decide whether the vapor pressure will be greater than that predicted by Raoult’s law (positive deviation), approximately equal to that predicted by Raoult’s law (an ideal solution), or less than the pressure predicted by Raoult’s law (negative deviation).
- cyclohexane and ethanol
- methanol and acetone
- n-hexane and isooctane (2,2,4-trimethylpentane)
Given: identity of pure liquids
Asked for: predicted deviation from Raoult’s law
Strategy:
Identify whether each liquid is polar or nonpolar, and then predict the type of intermolecular interactions that occur in solution.
Solution:
- Liquid ethanol contains an extensive hydrogen bonding network, and cyclohexane is nonpolar. Because the cyclohexane molecules cannot interact favorably with the polar ethanol molecules, they will disrupt the hydrogen bonding. Hence the A–B interactions will be weaker than the A–A and B–B interactions, leading to a higher vapor pressure than predicted by Raoult’s law (a positive deviation).
- Methanol contains an extensive hydrogen bonding network, but in this case the polar acetone molecules create A–B interactions that are stronger than the A–A or B–B interactions, leading to a negative enthalpy of solution and a lower vapor pressure than predicted by Raoult’s law (a negative deviation).
- Hexane and isooctane are both nonpolar molecules (isooctane actually has a very small dipole moment, but it is so small that it can be ignored). Hence the predominant intermolecular forces in both liquids are London dispersion forces. We expect the A–B interactions to be comparable in strength to the A–A and B–B interactions, leading to a vapor pressure in good agreement with that predicted by Raoult’s law (an ideal solution).
Exercise
For each system, compare the intermolecular interactions in the pure liquids with those in the solution to decide whether the vapor pressure will be greater than that predicted by Raoult’s law (positive deviation), approximately equal to that predicted by Raoult’s law (an ideal solution), or less than the pressure predicted by Raoult’s law (negative deviation):
- benzene and n-hexane
- ethylene glycol and CCl4
- acetic acid and n-propanol
Answer:
- approximately equal
- positive deviation (vapor pressure greater than predicted)
- negative deviation (vapor pressure less than predicted)
Boiling Point Elevation
Recall from Chapter 11 "Liquids" that the normal boiling point of a substance is the temperature at which the vapor pressure equals 1 atm. If a nonvolatile solute lowers the vapor pressure of a solvent, it must also affect the boiling point. Because the vapor pressure of the solution at a given temperature is less than the vapor pressure of the pure solvent, achieving a vapor pressure of 1 atm for the solution requires a higher temperature than the normal boiling point of the solvent. Thus the boiling point of a solution is always greater than that of the pure solvent. We can see why this must be true by comparing the phase diagram for an aqueous solution with the phase diagram for pure water (Figure 13.16 "Phase Diagrams of Pure Water and an Aqueous Solution of a Nonvolatile Solute"). The vapor pressure of the solution is less than that of pure water at all temperatures. Consequently, the liquid–vapor curve for the solution crosses the horizontal line corresponding to P = 1 atm at a higher temperature than does the curve for pure water.
Note the Pattern
The boiling point of a solution with a nonvolatile solute is always greater than the boiling point of the pure solvent.
Figure 13.16 Phase Diagrams of Pure Water and an Aqueous Solution of a Nonvolatile Solute
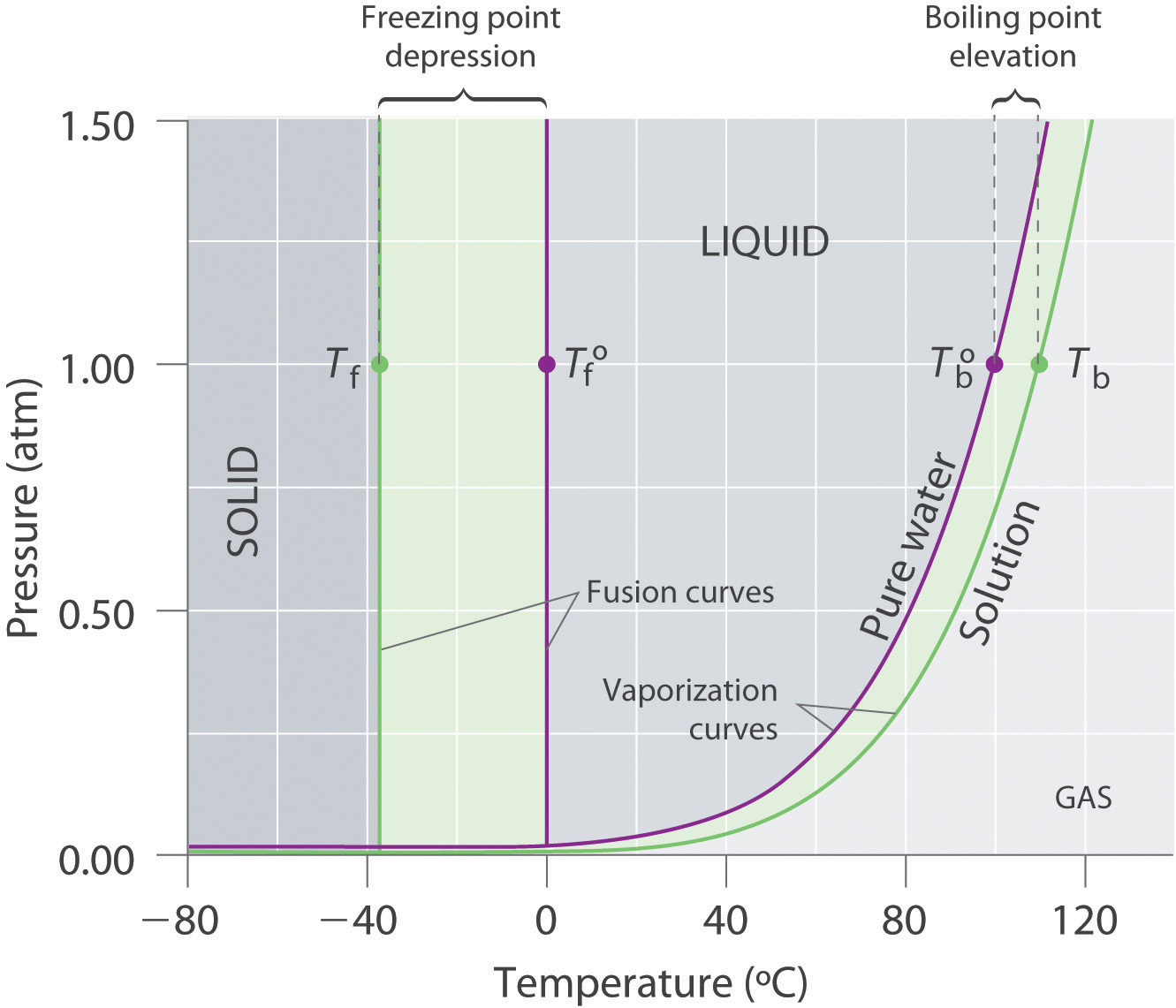
The vaporization curve for the solution lies below the curve for pure water at all temperatures, which results in an increase in the boiling point and a decrease in the freezing point of the solution.
The magnitude of the increase in the boiling point is related to the magnitude of the decrease in the vapor pressure. As we have just discussed, the decrease in the vapor pressure is proportional to the concentration of the solute in the solution. Hence the magnitude of the increase in the boiling point must also be proportional to the concentration of the solute (Figure 13.17 "Vapor Pressure Decrease and Boiling Point Increase as Functions of the Mole Fraction of a Nonvolatile Solute"). We can define the boiling point elevation (ΔTb)The difference between the boiling point of a solution and the boiling point of the pure solvent. as the difference between the boiling points of the solution and the pure solvent:
Equation 13.18
where Tb is the boiling point of the solution and is the boiling point of the pure solvent. We can express the relationship between ΔTb and concentration as follows:
Equation 13.19
ΔTb = mKbwhere m is the concentration of the solute expressed in molality, and Kb is the molal boiling point elevation constant of the solvent, which has units of °C/m. Table 13.7 "Boiling Point Elevation Constants (" lists characteristic Kb values for several commonly used solvents.
Figure 13.17 Vapor Pressure Decrease and Boiling Point Increase as Functions of the Mole Fraction of a Nonvolatile Solute
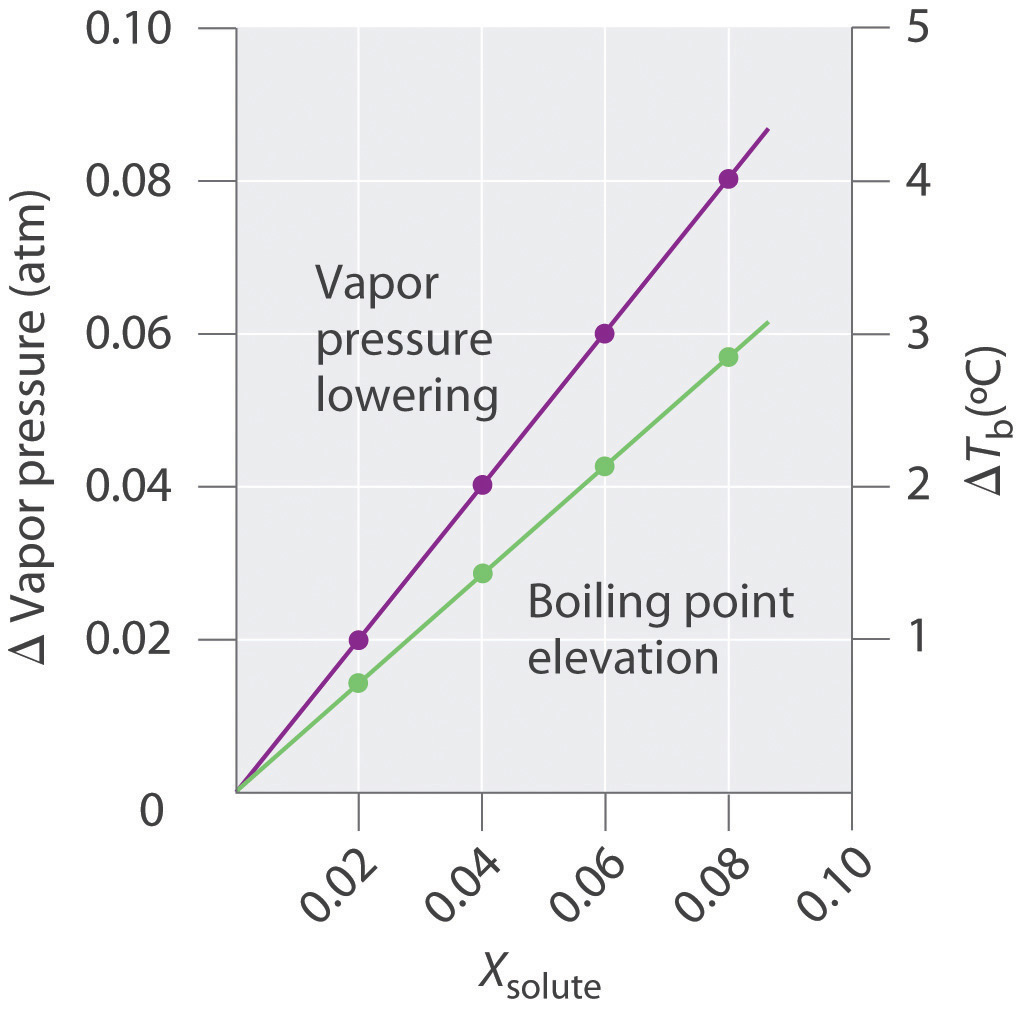
For relatively dilute solutions, the magnitude of both properties is proportional to the solute concentration.
Table 13.7 Boiling Point Elevation Constants (Kb) and Freezing Point Depression Constants (Kf) for Some Solvents
| Solvent | Boiling Point (°C) | Kb (°C/m) | Freezing Point (°C) | Kf (°C/m) |
|---|---|---|---|---|
| acetic acid | 117.90 | 3.22 | 16.64 | 3.63 |
| benzene | 80.09 | 2.64 | 5.49 | 5.07 |
| d-(+)-camphor | 207.4 | 4.91 | 178.8 | 37.8 |
| carbon disulfide | 46.2 | 2.42 | −112.1 | 3.74 |
| carbon tetrachloride | 76.8 | 5.26 | −22.62 | 31.4 |
| chloroform | 61.17 | 3.80 | −63.41 | 4.60 |
| nitrobenzene | 210.8 | 5.24 | 5.70 | 6.87 |
| water | 100.00 | 0.51 | 0.00 | 1.86 |
The concentration of the solute is typically expressed as molality rather than mole fraction or molarity for two reasons. First, because the density of a solution changes with temperature, the value of molarity also varies with temperature. If the boiling point depends on the solute concentration, then by definition the system is not maintained at a constant temperature. Second, molality and mole fraction are proportional for relatively dilute solutions, but molality has a larger numerical value (a mole fraction can be only between zero and one). Using molality allows us to eliminate nonsignificant zeros.
According to Table 13.7 "Boiling Point Elevation Constants (", the molal boiling point elevation constant for water is 0.51°C/m. Thus a 1.00 m aqueous solution of a nonvolatile molecular solute such as glucose or sucrose will have an increase in boiling point of 0.51°C, to give a boiling point of 100.51°C at 1.00 atm. The increase in the boiling point of a 1.00 m aqueous NaCl solution will be approximately twice as large as that of the glucose or sucrose solution because 1 mol of NaCl produces 2 mol of dissolved ions. Hence a 1.00 m NaCl solution will have a boiling point of about 101.02°C.
Example 10
In Example 8, we calculated that the vapor pressure of a 30.2% aqueous solution of ethylene glycol at 100°C is 85.1 mmHg less than the vapor pressure of pure water. We stated (without offering proof) that this should result in a higher boiling point for the solution compared with pure water. Now that we have seen why this assertion is correct, calculate the boiling point of the aqueous ethylene glycol solution.
Given: composition of solution
Asked for: boiling point
Strategy:
Calculate the molality of ethylene glycol in the 30.2% solution. Then use Equation 13.19 to calculate the increase in boiling point.
Solution:
From Example 8, we know that a 30.2% solution of ethylene glycol in water contains 302 g of ethylene glycol (4.87 mol) per 698 g of water. The molality of the solution is thus
From Equation 13.19, the increase in boiling point is therefore
The boiling point of the solution is thus predicted to be 104°C. With a solute concentration of almost 7 m, however, the assumption of a dilute solution used to obtain Equation 13.19 may not be valid.
Exercise
Assume that a tablespoon (5.00 g) of NaCl is added to 2.00 L of water at 20.0°C, which is then brought to a boil to cook spaghetti. At what temperature will the water boil?
Answer: 100.04°C, or 100°C to three significant figures. (Recall that 1 mol of NaCl produces 2 mol of dissolved particles. The small increase in temperature means that adding salt to the water used to cook pasta has essentially no effect on the cooking time.)
Freezing Point Depression
The phase diagram in Figure 13.16 "Phase Diagrams of Pure Water and an Aqueous Solution of a Nonvolatile Solute" shows that dissolving a nonvolatile solute in water not only raises the boiling point of the water but also lowers its freezing point. The solid–liquid curve for the solution crosses the line corresponding to P = 1 atm at a lower temperature than the curve for pure water.
We can understand this result by imagining that we have a sample of water at the normal freezing point temperature, where there is a dynamic equilibrium between solid and liquid. Water molecules are continuously colliding with the ice surface and entering the solid phase at the same rate that water molecules are leaving the surface of the ice and entering the liquid phase. If we dissolve a nonvolatile solute such as glucose in the liquid, the dissolved glucose molecules will reduce the number of collisions per unit time between water molecules and the ice surface because some of the molecules colliding with the ice will be glucose. Glucose, though, has a very different structure than water, and it cannot fit into the ice lattice. Consequently, the presence of glucose molecules in the solution can only decrease the rate at which water molecules in the liquid collide with the ice surface and solidify. Meanwhile, the rate at which the water molecules leave the surface of the ice and enter the liquid phase is unchanged. The net effect is to cause the ice to melt. The only way to reestablish a dynamic equilibrium between solid and liquid water is to lower the temperature of the system, which decreases the rate at which water molecules leave the surface of the ice crystals until it equals the rate at which water molecules in the solution collide with the ice.
By analogy to our treatment of boiling point elevation, the freezing point depression (ΔTf)The difference between the freezing point of a pure solvent and the freezing point of the solution. is defined as the difference between the freezing point of the pure solvent and the freezing point of the solution:
Equation 13.20
where is the freezing point of the pure solvent and Tf is the freezing point of the solution. The order of the terms is reversed compared with Equation 13.18 to express the freezing point depression as a positive number. The relationship between ΔTf and the solute concentration is given by an equation analogous to Equation 13.19:
Equation 13.21
ΔTf = mKfwhere m is the molality of the solution and Kf is the molal freezing point depression constant for the solvent (in units of °C/m). Like Kb, each solvent has a characteristic value of Kf (see Table 13.7 "Boiling Point Elevation Constants ("). Freezing point depression depends on the total number of dissolved nonvolatile solute particles, just as with boiling point elevation. Thus an aqueous NaCl solution has twice as large a freezing point depression as a glucose solution of the same molality.
People who live in cold climates use freezing point depression to their advantage in many ways. For example, salt is used to melt ice and snow on roads and sidewalks, ethylene glycol is added to engine coolant water to prevent an automobile engine from being destroyed, and methanol is added to windshield washer fluid to prevent the fluid from freezing.
Note the Pattern
The decrease in vapor pressure, increase in boiling point, and decrease in freezing point of a solution versus a pure liquid all depend on the total number of dissolved nonvolatile solute particles.
Example 11
In colder regions of the United States, NaCl or CaCl2 is often sprinkled on icy roads in winter to melt the ice and make driving safer. Use the data in Figure 13.9 "Solubilities of Several Inorganic and Organic Solids in Water as a Function of Temperature" to estimate the concentrations of two saturated solutions at 0°C, one of NaCl and one of CaCl2, and calculate the freezing points of both solutions to see which salt is likely to be more effective at melting ice.
Given: solubilities of two compounds
Asked for: concentrations and freezing points
Strategy:
A Estimate the solubility of each salt in 100 g of water from Figure 13.9 "Solubilities of Several Inorganic and Organic Solids in Water as a Function of Temperature". Determine the number of moles of each in 100 g and calculate the molalities.
B Determine the concentrations of the dissolved salts in the solutions. Substitute these values into Equation 13.21 to calculate the freezing point depressions of the solutions.
Solution:
A From Figure 13.9 "Solubilities of Several Inorganic and Organic Solids in Water as a Function of Temperature", we can estimate the solubilities of NaCl and CaCl2 to be about 36 g and 60 g, respectively, per 100 g of water at 0°C. The corresponding concentrations in molality are
The lower formula mass of NaCl more than compensates for its lower solubility, resulting in a saturated solution that has a slightly higher concentration than CaCl2.
B Because these salts are ionic compounds that dissociate in water to yield two and three ions per formula unit of NaCl and CaCl2, respectively, the actual concentrations of the dissolved species in the two saturated solutions are 2 × 6.2 m = 12 m for NaCl and 3 × 5.4 m = 16 m for CaCl2. The resulting freezing point depressions can be calculated using Equation 13.21:
Because the freezing point of pure water is 0°C, the actual freezing points of the solutions are −22°C and −30°C, respectively. Note that CaCl2 is substantially more effective at lowering the freezing point of water because its solutions contain three ions per formula unit. In fact, CaCl2 is the salt usually sold for home use, and it is also often used on highways.
Because the solubilities of both salts decrease with decreasing temperature, the freezing point can be depressed by only a certain amount, regardless of how much salt is spread on an icy road. If the temperature is significantly below the minimum temperature at which one of these salts will cause ice to melt (say −35°C), there is no point in using salt until it gets warmer.
Exercise
Calculate the freezing point of the 30.2% solution of ethylene glycol in water whose vapor pressure and boiling point we calculated in Example 13.8 and Example 13.10.
Answer: −13.0°C
Example 12
Arrange these aqueous solutions in order of decreasing freezing points: 0.1 m KCl, 0.1 m glucose, 0.1 m SrCl2, 0.1 m ethylene glycol, 0.1 m benzoic acid, and 0.1 m HCl.
Given: molalities of six solutions
Asked for: relative freezing points
Strategy:
A Identify each solute as a strong, weak, or nonelectrolyte, and use this information to determine the number of solute particles produced.
B Multiply this number by the concentration of the solution to obtain the effective concentration of solute particles. The solution with the highest effective concentration of solute particles has the largest freezing point depression.
Solution:
A Because the molal concentrations of all six solutions are the same, we must focus on which of the substances are strong electrolytes, which are weak electrolytes, and which are nonelectrolytes to determine the actual numbers of particles in solution. KCl, SrCl2, and HCl are strong electrolytes, producing two, three, and two ions per formula unit, respectively. Benzoic acid is a weak electrolyte (approximately one particle per molecule), and glucose and ethylene glycol are both nonelectrolytes (one particle per molecule).
B The molalities of the solutions in terms of the total particles of solute are: KCl and HCl, 0.2 m; SrCl2, 0.3 m; glucose and ethylene glycol, 0.1 m; and benzoic acid, 0.1–0.2 m. Because the magnitude of the decrease in freezing point is proportional to the concentration of dissolved particles, the order of freezing points of the solutions is: glucose and ethylene glycol (highest freezing point, smallest freezing point depression) > benzoic acid > HCl = KCl > SrCl2.
Exercise
Arrange these aqueous solutions in order of increasing freezing points: 0.2 m NaCl, 0.3 m acetic acid, 0.1 m CaCl2, and 0.2 m sucrose.
Answer: 0.2 m NaCl (lowest freezing point) < 0.3 m acetic acid ≈ 0.1 m CaCl2 < 0.2 m sucrose (highest freezing point)
In biological systems, freezing plant and animal tissues produces ice crystals that rip cells apart, causing severe frostbite and degrading the quality of fish or meat. How, then, can living organisms survive in freezing climates, where we might expect that exposure to freezing temperatures would be fatal? Many organisms that live in cold climates are able to survive at temperatures well below freezing by synthesizing their own chemical antifreeze in concentrations that prevent freezing. Such substances are typically small organic molecules with multiple –OH groups analogous to ethylene glycol.
Colligative properties can also be used to determine the molar mass of an unknown compound. One method that can be carried out in the laboratory with minimal equipment is to measure the freezing point of a solution with a known mass of solute. This method is accurate for dilute solutions (≤1% by mass) because changes in the freezing point are usually large enough to measure accurately and precisely. By comparing Kb and Kf values in Table 13.7 "Boiling Point Elevation Constants (", we see that changes in the boiling point are smaller than changes in the freezing point for a given solvent. Boiling point elevations are thus more difficult to measure precisely. For this reason, freezing point depression is more commonly used to determine molar mass than is boiling point elevation. Because of its very large value of Kf (37.8°C/m), d-(+)-camphor (Table 13.7 "Boiling Point Elevation Constants (") is often used to determine the molar mass of organic compounds by this method.
Example 13
A 7.08 g sample of elemental sulfur is dissolved in 75.0 g of CS2 to create a solution whose freezing point is −113.5°C. Use these data to calculate the molar mass of elemental sulfur and thus the formula of the dissolved Sn molecules (i.e., what is the value of n?).
Given: masses of solute and solvent and freezing point
Asked for: molar mass and number of S atoms per molecule
Strategy:
A Use Equation 13.20, the measured freezing point of the solution, and the freezing point of CS2 from Table 13.7 "Boiling Point Elevation Constants (" to calculate the freezing point depression. Then use Equation 13.21 and the value of Kf from Table 13.7 "Boiling Point Elevation Constants (" to calculate the molality of the solution.
B From the calculated molality, determine the number of moles of solute present.
C Use the mass and number of moles of the solute to calculate the molar mass of sulfur in solution. Divide the result by the molar mass of atomic sulfur to obtain n, the number of sulfur atoms per mole of dissolved sulfur.
Solution:
A The first step is to calculate the freezing point depression using Equation 13.20:
Then Equation 13.21 gives
B The total number of moles of solute present in the solution is
C We now know that 0.708 g of elemental sulfur corresponds to 0.028 mol of solute. The molar mass of dissolved sulfur is thus
The molar mass of atomic sulfur is 32 g/mol, so there must be 260/32 = 8.1 sulfur atoms per mole, corresponding to a formula of S8.
Exercise
One of the byproducts formed during the synthesis of C60 is a deep red solid containing only carbon. A solution of 205 mg of this compound in 10.0 g of CCl4 has a freezing point of −23.38°C. What are the molar mass and most probable formula of the substance?
Answer: 847 g/mol; C70
Osmotic Pressure
Osmotic pressure is a colligative property of solutions that is observed using a semipermeable membraneA barrier with pores small enough to allow solvent molecules to pass through but not solute molecules or ions., a barrier with pores small enough to allow solvent molecules to pass through but not solute molecules or ions. The net flow of solvent through a semipermeable membrane is called osmosisThe net flow of solvent through a semipermeable membrane. (from the Greek osmós, meaning “push”). The direction of net solvent flow is always from the side with the lower concentration of solute to the side with the higher concentration.
Osmosis can be demonstrated using a U-tube like the one shown in Figure 13.18 "Osmotic Pressure", which contains pure water in the left arm and a dilute aqueous solution of glucose in the right arm. A net flow of water through the membrane occurs until the levels in the arms eventually stop changing, which indicates that equilibrium has been reached. The osmotic pressure (Π)The pressure difference between the two sides of a semipermeable membrane that separates a pure solvent from a solution prepared from the same solvent. of the glucose solution is the difference in the pressure between the two sides, in this case the heights of the two columns. Although the semipermeable membrane allows water molecules to flow through in either direction, the rate of flow is not the same in both directions because the concentration of water is not the same in the two arms. The net flow of water through the membrane can be prevented by applying a pressure to the right arm that is equal to the osmotic pressure of the glucose solution.
Figure 13.18 Osmotic Pressure
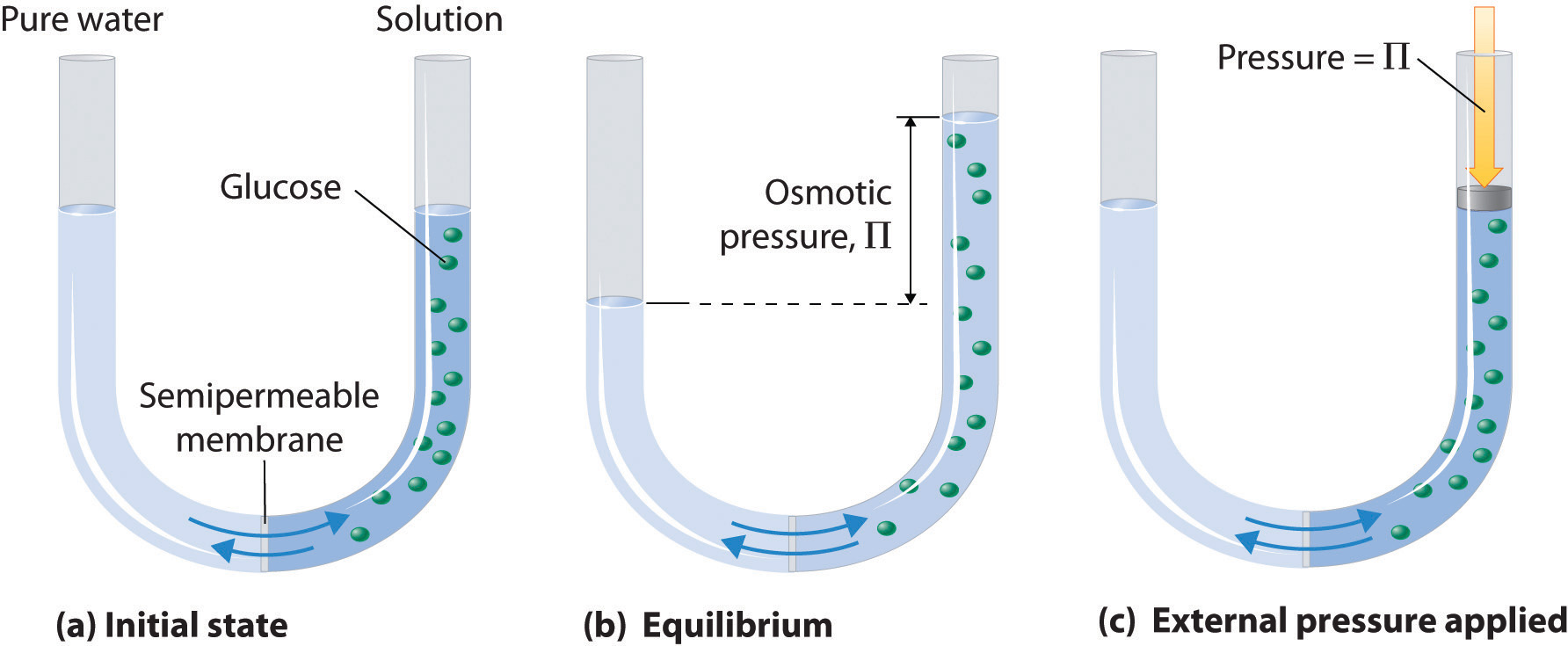
(a) A dilute solution of glucose in water is placed in the right arm of a U-tube, and the left arm is filled to the same height with pure water; a semipermeable membrane separates the two arms. Because the flow of pure solvent through the membrane from left to right (from pure water to the solution) is greater than the flow of solvent in the reverse direction, the level of liquid in the right tube rises. (b) At equilibrium, the pressure differential, equal to the osmotic pressure of the solution (Πsoln), equalizes the flow rate of solvent in both directions. (c) Applying an external pressure equal to the osmotic pressure of the original glucose solution to the liquid in the right arm reverses the flow of solvent and restores the original situation.
Just as with any other colligative property, the osmotic pressure of a solution depends on the concentration of dissolved solute particles. Osmotic pressure obeys a law that resembles the ideal gas equation:
Equation 13.22
where M is the number of moles of solute per unit volume of solution (i.e., the molarity of the solution), R is the ideal gas constant, and T is the absolute temperature. As shown in Example 14, osmotic pressures tend to be quite high, even for rather dilute solutions.
Example 14
When placed in a concentrated salt solution, certain yeasts are able to produce high internal concentrations of glycerol to counteract the osmotic pressure of the surrounding medium. Suppose that the yeast cells are placed in an aqueous solution containing 4.0% NaCl by mass; the solution density is 1.02 g/mL at 25°C.
- Calculate the osmotic pressure of a 4.0% aqueous NaCl solution at 25°C.
- If the normal osmotic pressure inside a yeast cell is 7.3 atm, corresponding to a total concentration of dissolved particles of 0.30 M, what concentration of glycerol must the cells synthesize to exactly balance the external osmotic pressure at 25°C?
Given: concentration, density, and temperature of NaCl solution; internal osmotic pressure of cell
Asked for: osmotic pressure of NaCl solution and concentration of glycerol needed
Strategy:
A Calculate the molarity of the NaCl solution using the formula mass of the solute and the density of the solution. Then calculate the total concentration of dissolved particles.
B Use Equation 13.22 to calculate the osmotic pressure of the solution.
C Subtract the normal osmotic pressure of the cells from the osmotic pressure of the salt solution to obtain the additional pressure needed to balance the two. Use Equation 13.22 to calculate the molarity of glycerol needed to create this osmotic pressure.
Solution:
-
A The solution contains 4.0 g of NaCl per 100 g of solution. Using the formula mass of NaCl (58.44 g/mol) and the density of the solution (1.02 g/mL), we can calculate the molarity:
Because 1 mol of NaCl produces 2 mol of particles in solution, the total concentration of dissolved particles in the solution is (2)(0.70 M) = 1.4 M.
B Now we can use Equation 13.22 to calculate the osmotic pressure of the solution:
-
C If the yeast cells are to exactly balance the external osmotic pressure, they must produce enough glycerol to give an additional internal pressure of (34 atm − 7.3 atm) = 27 atm. Glycerol is a nonelectrolyte, so we can solve Equation 13.22 for the molarity corresponding to this osmotic pressure:
In solving this problem, we could also have recognized that the only way the osmotic pressures can be the same inside the cells and in the solution is if the concentrations of dissolved particles are the same. We are given that the normal concentration of dissolved particles in the cells is 0.3 M, and we have calculated that the NaCl solution is effectively 1.4 M in dissolved particles. The yeast cells must therefore synthesize enough glycerol to increase the internal concentration of dissolved particles from 0.3 M to 1.4 M—that is, an additional 1.1 M concentration of glycerol.
Exercise
Assume that the fluids inside a sausage are approximately 0.80 M in dissolved particles due to the salt and sodium nitrite used to prepare them. Calculate the osmotic pressure inside the sausage at 100°C to learn why experienced cooks pierce the semipermeable skin of sausages before boiling them.
Answer: 24 atm
Because of the large magnitude of osmotic pressures, osmosis is extraordinarily important in biochemistry, biology, and medicine. Virtually every barrier that separates an organism or cell from its environment acts like a semipermeable membrane, permitting the flow of water but not solutes. The same is true of the compartments inside an organism or cell. Some specialized barriers, such as those in your kidneys, are slightly more permeable and use a related process called dialysisA process that uses a semipermeable membrane with pores large enough to allow small solute molecules and solvent molecules to pass through but not large solute molecules., which permits both water and small molecules to pass through but not large molecules such as proteins.
The same principle has long been used to preserve fruits and their essential vitamins over the long winter. High concentrations of sugar are used in jams and jellies not for sweetness alone but because they greatly increase the osmotic pressure. Thus any bacteria not killed in the cooking process are dehydrated, which keeps them from multiplying in an otherwise rich medium for bacterial growth. A similar process using salt prevents bacteria from growing in ham, bacon, salt pork, salt cod, and other preserved meats. The effect of osmotic pressure is dramatically illustrated in Figure 13.19 "Effect on Red Blood Cells of the Surrounding Solution’s Osmotic Pressure", which shows what happens when red blood cells are placed in a solution whose osmotic pressure is much lower or much higher than the internal pressure of the cells.
Figure 13.19 Effect on Red Blood Cells of the Surrounding Solution’s Osmotic Pressure
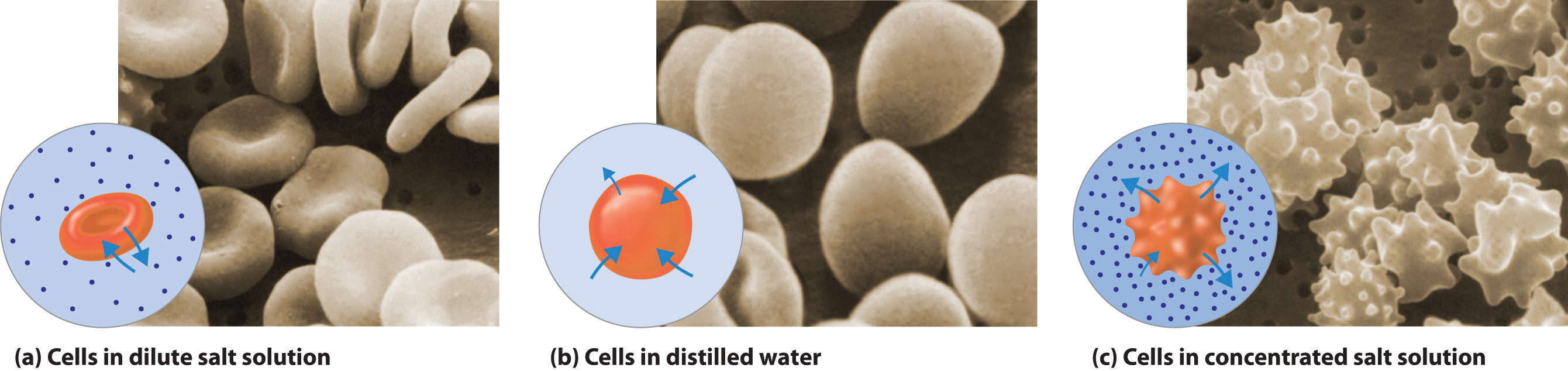
(a) When red blood cells are placed in a dilute salt solution having the same osmotic pressure as the intracellular fluid, the rate of flow of water into and out of the cells is the same and their shape does not change. (b) When cells are placed in distilled water whose osmotic pressure is less than that of the intracellular fluid, the rate of flow of water into the cells is greater than the rate of flow out of the cells. The cells swell and eventually burst. (c) When cells are placed in a concentrated salt solution with an osmotic pressure greater than that of the intracellular fluid, the rate of flow of water out of the cells is greater than the rate of flow into the cells. The cells shrivel and become so deformed that they cannot function.
In addition to capillary action, trees use osmotic pressure to transport water and other nutrients from the roots to the upper branches. (For more information about capillary action, see Chapter 11 "Liquids", Section 11.3 "Unique Properties of Liquids".) Evaporation of water from the leaves results in a local increase in the salt concentration, which generates an osmotic pressure that pulls water up the trunk of the tree to the leaves.
Finally, a process called reverse osmosisA process that uses the application of an external pressure greater than the osmotic pressure of a solution to reverse the flow of solvent through the semipermeable membrane. can be used to produce pure water from seawater. As shown schematically in Figure 13.20 "Desalinization of Seawater by Reverse Osmosis", applying high pressure to seawater forces water molecules to flow through a semipermeable membrane that separates pure water from the solution, leaving the dissolved salt behind. Large-scale desalinization plants that can produce hundreds of thousands of gallons of freshwater per day are common in the desert lands of the Middle East, where they supply a large proportion of the freshwater needed by the population. Similar facilities are now being used to supply freshwater in southern California. Small, hand-operated reverse osmosis units can produce approximately 5 L of freshwater per hour, enough to keep 25 people alive, and are now standard equipment on US Navy lifeboats.
Figure 13.20 Desalinization of Seawater by Reverse Osmosis
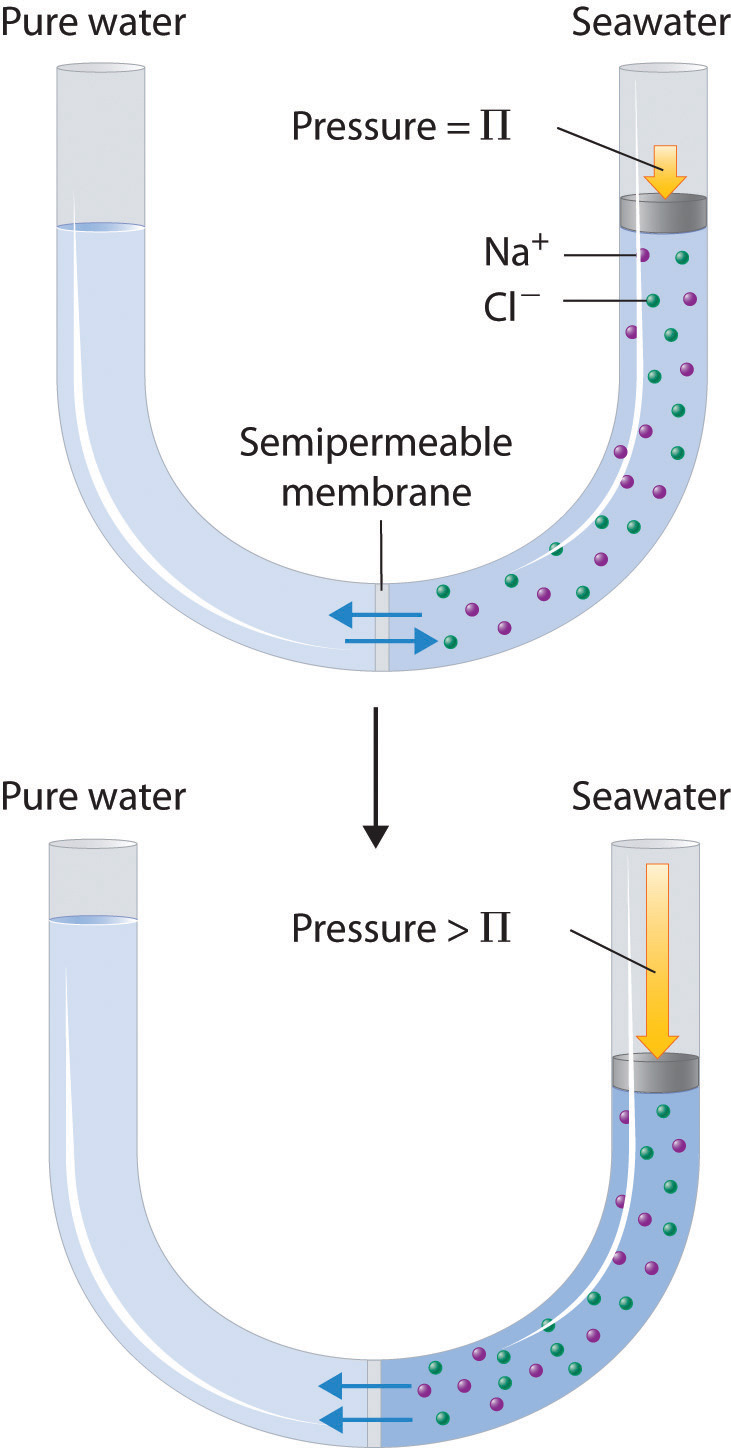
(top) When the pressure applied to seawater equals its osmotic pressure (Πsoln), there is no net flow of water across the semipermeable membrane. (bottom) The application of pressure greater than the osmotic pressure of seawater forces water molecules to flow through the membrane, leaving behind a concentrated salt solution. In desalinization plants, seawater is continuously introduced under pressure and pure water is collected, so the process continues indefinitely.
Colligative Properties of Electrolyte Solutions
Thus far we have assumed that we could simply multiply the molar concentration of a solute by the number of ions per formula unit to obtain the actual concentration of dissolved particles in an electrolyte solution. We have used this simple model to predict such properties as freezing points, melting points, vapor pressure, and osmotic pressure. If this model were perfectly correct, we would expect the freezing point depression of a 0.10 m solution of sodium chloride, with 2 mol of ions per mole of NaCl in solution, to be exactly twice that of a 0.10 m solution of glucose, with only 1 mol of molecules per mole of glucose in solution. In reality, this is not always the case. Instead, the observed change in freezing points for 0.10 m aqueous solutions of NaCl and KCl are significantly less than expected (−0.348°C and −0.344°C, respectively, rather than −0.372°C), which suggests that fewer particles than we expected are present in solution.
The relationship between the actual number of moles of solute added to form a solution and the apparent number as determined by colligative properties is called the van’t Hoff factor(i)The ratio of the apparent number of particles in solution to the number predicted by the stoichiometry of the salt. and is defined as follows:Named for Jacobus Hendricus van’t Hoff (1852–1911), a Dutch chemistry professor at the University of Amsterdam who won the first Nobel Prize in Chemistry (1901) for his work on thermodynamics and solutions.
Equation 13.23
Note the Pattern
As the solute concentration increases the van’t Hoff factor decreases.
The van’t Hoff factor is therefore a measure of a deviation from ideal behavior. The lower the van’t Hoff factor, the greater the deviation. As the data in Table 13.8 "van’t Hoff Factors for 0.0500 M Aqueous Solutions of Selected Compounds at 25°C" show, the van’t Hoff factors for ionic compounds are somewhat lower than expected; that is, their solutions apparently contain fewer particles than predicted by the number of ions per formula unit. As the concentration of the solute increases, the van’t Hoff factor decreases because ionic compounds generally do not totally dissociate in aqueous solution. Instead, some of the ions exist as ion pairsA cation and anion that are in intimate contact in solution rather than separated by solvent and that migrates in solution as a single unit., a cation and an anion that for a brief time are associated with each other without an intervening shell of water molecules (Figure 13.21 "Ion Pairs"). Each of these temporary units behaves like a single dissolved particle until it dissociates. Highly charged ions such as Mg2+, Al3+, SO42−, and PO43− have a greater tendency to form ion pairs because of their strong electrostatic interactions. The actual number of solvated ions present in a solution can be determined by measuring a colligative property at several solute concentrations.
Figure 13.21 Ion Pairs
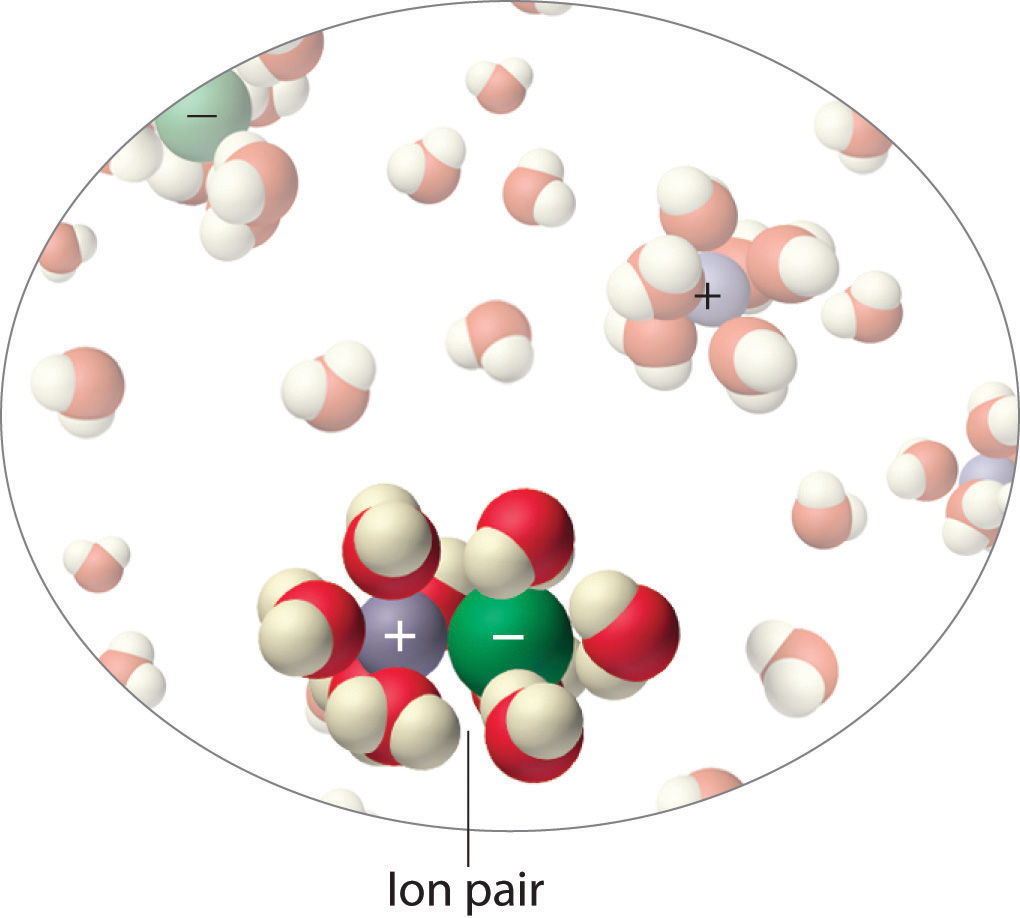
In concentrated solutions of electrolytes like NaCl, some of the ions form neutral ion pairs that are not separated by solvent and diffuse as single particles.
Table 13.8 van’t Hoff Factors for 0.0500 M Aqueous Solutions of Selected Compounds at 25°C
| Compound | i (measured) | i (ideal) |
|---|---|---|
| glucose | 1.0 | 1.0 |
| sucrose | 1.0 | 1.0 |
| NaCl | 1.9 | 2.0 |
| HCl | 1.9 | 2.0 |
| MgCl2 | 2.7 | 3.0 |
| FeCl3 | 3.4 | 4.0 |
| Ca(NO3)2 | 2.5 | 3.0 |
| AlCl3 | 3.2 | 4.0 |
| MgSO4 | 1.4 | 2.0 |
Example 15
A 0.0500 M aqueous solution of FeCl3 has an osmotic pressure of 4.15 atm at 25°C. Calculate the van’t Hoff factor i for the solution.
Given: solute concentration, osmotic pressure, and temperature
Asked for: van’t Hoff factor
Strategy:
A Use Equation 13.22 to calculate the expected osmotic pressure of the solution based on the effective concentration of dissolved particles in the solvent.
B Calculate the ratio of the observed osmotic pressure to the expected value. Multiply this number by the number of ions of solute per formula unit, and then use Equation 13.23 to calculate the van’t Hoff factor.
Solution:
A If FeCl3 dissociated completely in aqueous solution, it would produce four ions per formula unit [Fe3+(aq) plus 3Cl−(aq)] for an effective concentration of dissolved particles of 4 × 0.0500 M = 0.200 M. The osmotic pressure would be
B The observed osmotic pressure is only 4.15 atm, presumably due to ion pair formation. The ratio of the observed osmotic pressure to the calculated value is 4.15 atm/4.89 atm = 0.849, which indicates that the solution contains (0.849)(4) = 3.40 particles per mole of FeCl3 dissolved. Alternatively, we can calculate the observed particle concentration from the osmotic pressure of 4.15 atm:
The ratio of this value to the expected value of 0.200 M is 0.170 M/0.200 M = 0.850, which again gives us (0.850)(4) = 3.40 particles per mole of FeCl3 dissolved. From Equation 13.23, the van’t Hoff factor for the solution is
Exercise
Calculate the van’t Hoff factor for a 0.050 m aqueous solution of MgCl2 that has a measured freezing point of −0.25°C.
Answer: 2.7 (versus an ideal value of 3)
Summary
The colligative properties of a solution depend on only the total number of dissolved particles in solution, not on their chemical identity. Colligative properties include vapor pressure, boiling point, freezing point, and osmotic pressure. The addition of a nonvolatile solute (one without a measurable vapor pressure) decreases the vapor pressure of the solvent. The vapor pressure of the solution is proportional to the mole fraction of solvent in the solution, a relationship known as Raoult’s law. Solutions that obey Raoult’s law are called ideal solutions. Most real solutions exhibit positive or negative deviations from Raoult’s law. The boiling point elevation (ΔTb) and freezing point depression (ΔTf) of a solution are defined as the differences between the boiling and freezing points, respectively, of the solution and the pure solvent. Both are proportional to the molality of the solute. When a solution and a pure solvent are separated by a semipermeable membrane, a barrier that allows solvent molecules but not solute molecules to pass through, the flow of solvent in opposing directions is unequal and produces an osmotic pressure, which is the difference in pressure between the two sides of the membrane. Osmosis is the net flow of solvent through such a membrane due to different solute concentrations. Dialysis uses a semipermeable membrane with pores that allow only small solute molecules and solvent molecules to pass through. In more concentrated solutions, or in solutions of salts with highly charged ions, the cations and anions can associate to form ion pairs, which decreases their effect on the colligative properties of the solution. The extent of ion pair formation is given by the van’t Hoff factor (i), the ratio of the apparent number of particles in solution to the number predicted by the stoichiometry of the salt.
Key Takeaway
- The total number of nonvolatile solute particles determines the decrease in vapor pressure, increase in boiling point, and decrease in freezing point of a solution versus the pure solvent.
Key Equations
Henry’s law
Equation 13.10: C = kP
Raoult’s law
vapor pressure lowering
vapor pressure of a system containing two volatile components
boiling point elevation
Equation 13.19: ΔTb = mKb
freezing point depression
Equation 13.21: ΔTf = mKf
osmotic pressure
van’t Hoff factor
Conceptual Problems
-
Why does the vapor pressure of a solvent decrease when adding a nonvolatile solute?
-
Does seawater boil at the same temperature as distilled water? If not, which has the higher boiling point? Explain your answer.
-
Which will be more soluble in benzene—O2 or HCl? Will H2S or HCl be more soluble in water? Explain your reasoning in each case.
-
Will the vapor pressure of a solution of hexane and heptane have an ideal vapor pressure curve (i.e., obey Raoult’s law)? Explain your answer. What properties of two liquids determine whether a solution of the two will exhibit an ideal behavior?
-
Predict whether the following mixtures will exhibit negative, zero, or positive deviations from Raoult’s law. Explain your reasoning in each case.
- carbon tetrachloride and heptane
- methanol and tetrahydrofuran (C4H8O)
- acetone [(CH3)2C=CO] and dichloromethane
- hexane and methanol
-
Why are deviations from the ideal behavior predicted by Raoult’s law more common for solutions of liquids than are deviations from the ideal behavior predicted by the ideal gas law for solutions of gases?
-
Boiling point elevation is proportional to the molal concentration of the solute. Is it also proportional to the molar concentration of the solution? Why or why not?
-
Many packaged foods in sealed bags are cooked by placing the bag in boiling water. How could you reduce the time required to cook the contents of the bag using this cooking method?
-
If the costs per kilogram of ethylene glycol and of ethanol were the same, which would be the more cost-effective antifreeze?
-
Many people get thirsty after eating foods such as ice cream or potato chips that have a high sugar or salt content, respectively. Suggest an explanation for this phenomenon.
-
When two aqueous solutions with identical concentrations are separated by a semipermeable membrane, no net movement of water occurs. What happens when a solute that cannot penetrate the membrane is added to one of the solutions? Why?
-
A solution injected into blood vessels must have an electrolyte concentration nearly identical to that found in blood plasma. Why? What would happen if red blood cells were placed in distilled water? What would happen to red blood cells if they were placed in a solution that had twice the electrolyte concentration of blood plasma?
-
If you were stranded on a desert island, why would drinking seawater lead to an increased rate of dehydration, eventually causing you to die of thirst?
-
What is the relationship between the van’t Hoff factor for a compound and its lattice energy?
Numerical Problems
-
Hemoglobin is the protein that is responsible for the red color of blood and for transporting oxygen from the lungs to the tissues. A solution with 11.2 mg of hemoglobin per mL has an osmotic pressure of 2.9 mmHg at 5°C. What is the molecular mass of hemoglobin?
-
To determine the molar mass of the antifreeze protein from the Arctic right-eye flounder, the osmotic pressure of a solution containing 13.2 mg of protein per mL was measured and found to be 21.2 mmHg at 10°C. What is the molar mass of the protein?
-
What is the osmotic pressure at 21.0°C of 13.5 mL of a solution with 1.77 g of sucrose (C12H22O11)?
-
A solution of NaNO3 is generated by dissolving 1.25 g of NaNO3 in enough water to give a final volume of 25.0 mL. What is the osmotic pressure of this sample at 25.0°C?
-
Which would have the lower vapor pressure—an aqueous solution that is 0.12 M in glucose or one that is 0.12 M in CaCl2? Why?
-
What is the total particle concentration expected for each aqueous solution? Which would produce the highest osmotic pressure?
- 0.35 M KBr
- 0.11 M MgSO4
- 0.26 M MgCl2
- 0.24 M glucose (C6H12O6)
-
The boiling point of an aqueous solution of sodium chloride is 100.37°C. What is the molality of the solution? How many grams of NaCl are present in 125 g of the solution?
-
Calculate the boiling point of a solution of sugar prepared by dissolving 8.4 g of glucose (C6H12O6) in 250 g of water.
-
At 37°C, the vapor pressure of 300.0 g of water was reduced from 0.062 atm to 0.058 atm by the addition of NaBr. How many grams of NaBr were added?
-
How many grams of KCl must be added to reduce the vapor pressure of 500.0 g of H2O from 17.5 mmHg to 16.0 mmHg at 20.0°C?
-
How much NaCl would you have to add to 2.0 L of water at a mountain lodge at an elevation of 7350 ft, where the pressure is 0.78 atm and the boiling point of water is 94°C, to get the water to boil at the same temperature as in New Orleans, Louisiana, where the pressure is 1.00 atm?
-
You have three solutions with the following compositions: 12.5 g of KCl in 250 mL of water, 12.5 g of glucose in 400 mL of water, and 12.5 g of MgCl2 in 350 mL of water. Which will have the highest boiling point?
-
Assuming the price per kilogram is the same, which is a better salt to use for deicing wintry roads—NaCl or MgCl2? Why? Would magnesium chloride be an effective deicer at a temperature of −8°C?
-
How many grams of KNO3 must be added to water to produce the same boiling point elevation as a solution of 2.03 g of MgCl2 in a total volume of 120.0 mL of solution, assuming complete dissociation? If the van’t Hoff factor for MgCl2 at this concentration is 2.73, how much KNO3 would be needed?
-
Calculate the quantity of each compound that would need to be added to lower the freezing point of 500.0 mL of water by 1.0°C: KBr, ethylene glycol, MgBr2, ethanol. Assume that the density of water is 1.00 g/cm3.
-
The melting point depression of biphenyl (melting point = 69.0°C) can be used to determine the molecular mass of organic compounds. A mixture of 100.0 g of biphenyl and 2.67 g of naphthalene (C10H8) has a melting point of 68.50°C. If a mixture of 1.00 g of an unknown compound with 100.0 g of biphenyl has a melting point of 68.86°C, what is the molar mass of the unknown compound?
-
Four solutions of urea in water were prepared, with concentrations of 0.32 m, 0.55 m, 1.52 m, and 3.16 m. The freezing points of these solutions were found to be −0.595°C, −1.02°C, −2.72°C, and −5.71°C, respectively. Graphically determine the freezing point depression constant for water. A fifth solution made by dissolving 6.22 g of urea in 250.0 g of water has a freezing point of −0.75°C. Use these data to determine the molar mass of urea.
-
The term osmolarity has been used to describe the total solute concentration of a solution (generally water), where 1 osmole (Osm) is equal to 1 mol of an ideal, nonionizing molecule.
- What is the osmolarity of a 1.5 M solution of glucose? a 1.5 M solution of NaCl? a 1.5 M solution of CaCl2?
- What is the relationship between osmolarity and the concentration of water?
- What would be the direction of flow of water through a semipermeable membrane separating a 0.1 M solution of NaCl and a 0.1 M solution of CaCl2?
-
At 40°C, the vapor pressures of pure CCl4 and cyclohexane are 0.2807 atm and 0.2429 atm, respectively. Assuming ideal behavior, what is the vapor pressure of a solution with a CCl4 mole fraction of 0.475? What is the mole fraction of cyclohexane in the vapor phase? The boiling points of CCl4 and cyclohexane are 76.8°C and 80.7°C, respectively.
-
A benzene/toluene solution with a mole fraction of benzene of 0.6589 boils at 88°C at 1 atm. The vapor pressures of pure benzene and toluene at this temperature are 1.259 atm and 0.4993 atm, respectively. What is the composition of the vapor above the boiling solution at this temperature?
-
Plot the vapor pressure of the solution versus composition for the system CCl4–CH3CN at 45°C, given the following experimental data:
(liquid) 0.035 0.375 0.605 0.961 (vapor) 0.180 0.543 0.594 0.800 Total P (atm) 0.326 0.480 0.488 0.414 Source: Adapted from L. Brown and W. Foch, Australian Journal of Chemistry, 9 (1956): 180.
Does your diagram show behavior characteristic of an ideal solution? Explain your answer.
Answers
-
6.7 × 104 amu
-
-
9.24 atm
-
-
The CaCl2 solution will have a lower vapor pressure, because it contains three times as many particles as the glucose solution.
-
-
0.36 m NaCl, 2.6 g NaCl
-
-
60 g NaBr
-
-
700 g NaCl
-
-
MgCl2 produces three particles in solution versus two for NaCl, so the same molal concentration of MgCl2 will produce a 50% greater freezing point depression than for NaCl. Nonetheless, the molar mass of MgCl2 is 95.3 g/mol versus 48.45 g/mol for NaCl. Consequently, a solution containing 1 g NaCl per 1000 g H2O will produce a freezing point depression of 0.064°C versus 0.059°C for a solution containing 1 g MgCl2 per 1000 g H2O. Thus, given equal cost per gram, NaCl is more effective. Yes, MgCl2 would be effective at −8°C; a 1.43 m solution (136 g per 1000 g H2O) would be required.
-
-
-
-
kf = 1.81(°C·kg)/mol, molecular mass of urea = 60.0 g/mol
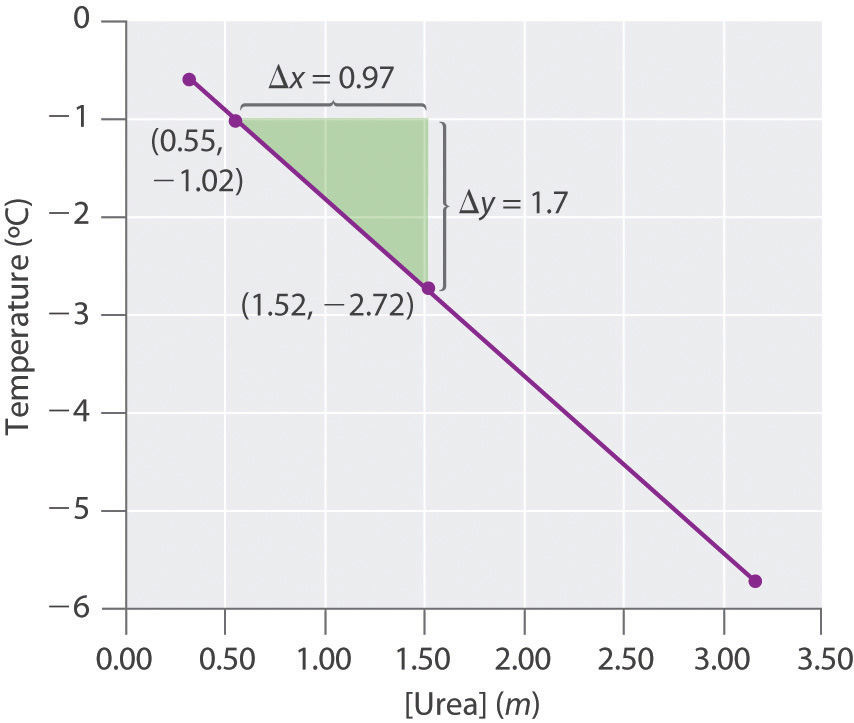
-
-
-
-
13.6 Aggregate Particles in Aqueous Solution
Learning Objective
- To distinguish between true solutions and solutions with aggregate particles.
Suspensions and colloids are two common types of mixtures whose properties are in many ways intermediate between those of true solutions and heterogeneous mixtures. A suspensionA heterogeneous mixture of particles with diameters of about 1 µm that are distributed throughout a second phase and that separate from the dispersing phase on standing. is a heterogeneous mixture of particles with diameters of about 1 µm (1000 nm) that are distributed throughout a second phase. Common suspensions include paint, blood, and hot chocolate, which are solid particles in a liquid, and aerosol sprays, which are liquid particles in a gas. If the suspension is allowed to stand, the two phases will separate, which is why paints must be thoroughly stirred or shaken before use. A colloidA heterogeneous mixture of particles with diameters of about 2–500 nm that are distributed throughout a second phase and do not separate from the dispersing phase on standing. is also a heterogeneous mixture, but the particles of a colloid are typically smaller than those of a suspension, generally in the range of 2 to about 500 nm in diameter. Colloids include fog and clouds (liquid particles in a gas), milk (solid particles in a liquid), and butter (solid particles in a solid). Other colloids are used industrially as catalysts. Unlike in a suspension, the particles in a colloid do not separate into two phases on standing. The only combination of substances that cannot produce a suspension or a colloid is a mixture of two gases because their particles are so small that they always form true solutions. The properties of suspensions, colloids, and solutions are summarized in Table 13.9 "Properties of Liquid Solutions, Colloids, and Suspensions".
Table 13.9 Properties of Liquid Solutions, Colloids, and Suspensions
| Type of Mixture | Approximate Size of Particles (nm) | Characteristic Properties | Examples |
|---|---|---|---|
| solution | < 2 | not filterable; does not separate on standing; does not scatter visible light | air, white wine, gasoline, salt water |
| colloid | 2–500 | scatters visible light; translucent or opaque; not filterable; does not separate on standing | smoke, fog, ink, milk, butter, cheese |
| suspension | 500–1000 | cloudy or opaque; filterable; separates on standing | muddy water, hot cocoa, blood, paint |
Colloids and Suspensions
Colloids were first characterized in about 1860 by Thomas Graham, who also gave us Graham’s law of diffusion and effusion. Although some substances, such as starch, gelatin, and glue, appear to dissolve in water to produce solutions, Graham found that they diffuse very slowly or not at all compared with solutions of substances such as salt and sugar. Graham coined the word colloid (from the Greek kólla, meaning “glue”) to describe these substances, as well as the words solA dispersion of solid particles in a liquid or solid. and gelA semisolid sol in which all of the liquid phase has been absorbed by the solid particles. to describe certain types of colloids in which all of the solvent has been absorbed by the solid particles, thus preventing the mixture from flowing readily, as we see in Jell-O. Two other important types of colloids are aerosolsA dispersion of solid or liquid particles in a gas., which are dispersions of solid or liquid particles in a gas, and emulsions, which are dispersions of one liquid in another liquid with which it is immiscible.
Colloids share many properties with solutions. For example, the particles in both are invisible without a powerful microscope, do not settle on standing, and pass through most filters. However, the particles in a colloid scatter a beam of visible light, a phenomenon known as the Tyndall effectThe phenomenon of scattering a beam of visible light.,The effect is named after its discoverer, John Tyndall, an English physicist (1820–1893). whereas the particles of a solution do not. The Tyndall effect is responsible for the way the beams from automobile headlights are clearly visible from the side on a foggy night but cannot be seen from the side on a clear night. It is also responsible for the colored rays of light seen in many sunsets, where the sun’s light is scattered by water droplets and dust particles high in the atmosphere. An example of the Tyndall effect is shown in Figure 13.22 "Tyndall Effect, the Scattering of Light by Colloids".
Figure 13.22 Tyndall Effect, the Scattering of Light by Colloids

Both cylinders contain a solution of red food coloring in water, but a small amount of gelatin has been added to the cylinder on the right to form a colloidal suspension of gelatin particles. The beam of light goes straight through the true solution on the left, but the light beam is scattered by the colloid on the right.
Although colloids and suspensions can have particles similar in size, the two differ in stability: the particles of a colloid remain dispersed indefinitely unless the temperature or chemical composition of the dispersing medium is changed. The chemical explanation for the stability of colloids depends on whether the colloidal particles are hydrophilic or hydrophobic.
Most proteins, including those responsible for the properties of gelatin and glue, are hydrophilic because their exterior surface is largely covered with polar or charged groups. Starch, a long-branched polymer of glucose molecules, is also hydrophilic. A hydrophilic colloid particle interacts strongly with water, resulting in a shell of tightly bound water molecules that prevents the particles from aggregating when they collide. Heating such a colloid can cause aggregation because the particles collide with greater energy and disrupt the protective shell of solvent. Moreover, heat causes protein structures to unfold, exposing previously buried hydrophobic groups that can now interact with other hydrophobic groups and cause the particles to aggregate and precipitate from solution. When an egg is boiled, for example, the egg white, which is primarily a colloidal suspension of a protein called albumin, unfolds and exposes its hydrophobic groups, which aggregate and cause the albumin to precipitate as a white solid.
In some cases, a stable colloid can be transformed to an aggregated suspension by a minor chemical modification. Consider, for example, the behavior of hemoglobin, a major component of red blood cells. Hemoglobin molecules normally form a colloidal suspension inside red blood cells, which typically have a “donut” shape and are easily deformed, allowing them to squeeze through the capillaries to deliver oxygen to tissues. In a common inherited disease called sickle-cell anemia, one of the amino acids in hemoglobin that has a hydrophilic carboxylic acid side chain (glutamate) is replaced by another amino acid that has a hydrophobic side chain (valine, Figure 5.16 "The Structures of 10 Amino Acids"). Under some conditions, the abnormal hemoglobin molecules can aggregate to form long, rigid fibers that cause the red blood cells to deform, adopting a characteristic sickle shape that prevents them from passing through the capillaries (Figure 13.23 "Sickle-Cell Anemia"). The reduction in blood flow results in severe cramps, swollen joints, and liver damage. Until recently, many patients with sickle-cell anemia died before the age of 30 from infection, blood clots, or heart or kidney failure, although individuals with the sickle-cell genetic trait are more resistant to malaria than are those with “normal” hemoglobin.
Figure 13.23 Sickle-Cell Anemia
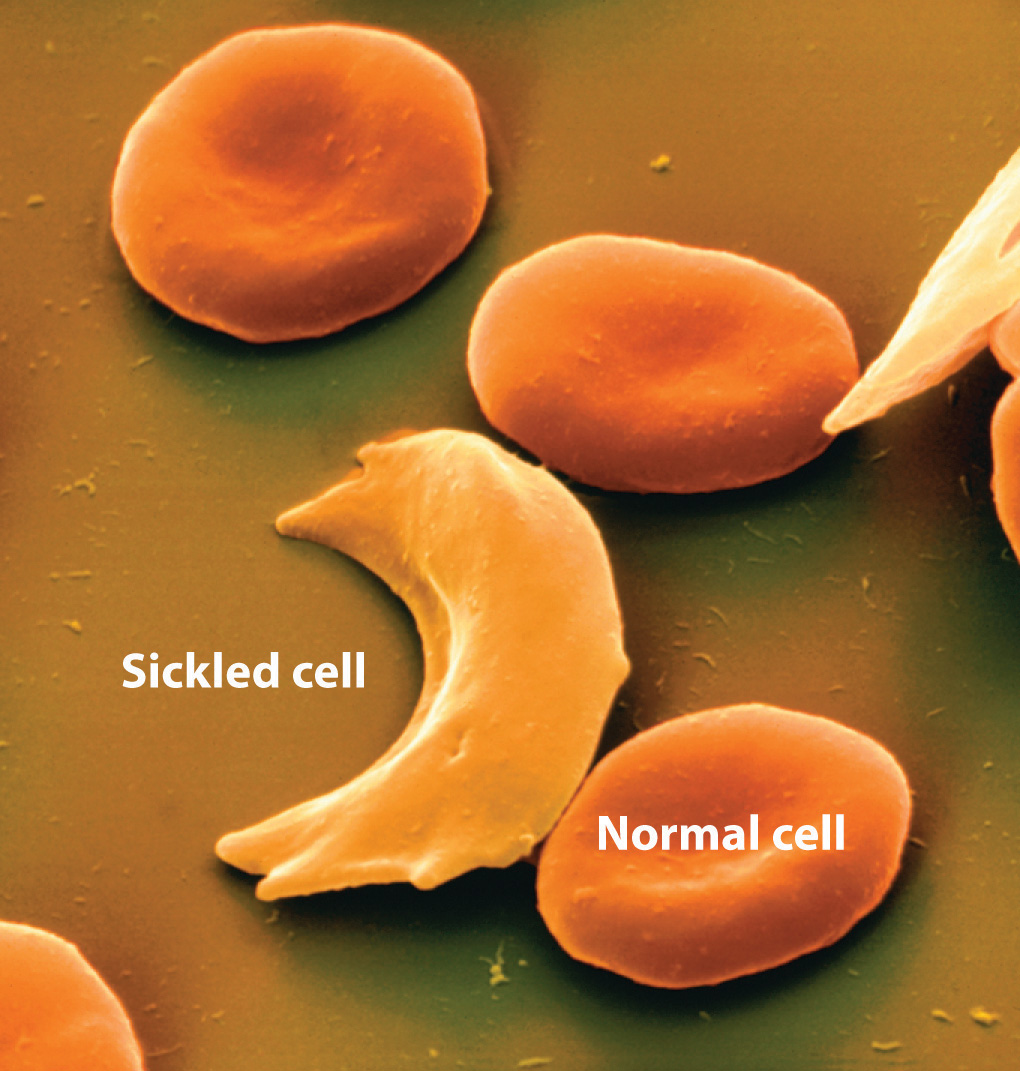
The characteristic shape of sickled red blood cells is the result of fibrous aggregation of hemoglobin molecules inside the cell.
Figure 13.24 Formation of New Land by the Destabilization of a Colloid Suspension

This satellite photograph shows the Mississippi River delta from New Orleans (top) to the Gulf of Mexico (bottom). Where seawater mixes with freshwater from the Mississippi River, colloidal clay particles in the river water precipitate (tan area).
Aggregation and precipitation can also result when the outer, charged layer of a particle is neutralized by ions with the opposite charge. In inland waterways, clay particles, which have a charged surface, form a colloidal suspension. High salt concentrations in seawater neutralize the charge on the particles, causing them to precipitate and form land at the mouths of large rivers, as seen in the satellite view in Figure 13.24 "Formation of New Land by the Destabilization of a Colloid Suspension". Charge neutralization is also an important strategy for precipitating solid particles from gaseous colloids such as smoke, and it is widely used to reduce particulate emissions from power plants that burn fossil fuels.
Emulsions
EmulsionsA dispersion of one liquid phase in another liquid with which it is immiscible. are colloids formed by the dispersion of a hydrophobic liquid in water, thereby bringing two mutually insoluble liquids, such as oil and water, in close contact. Various agents have been developed to stabilize emulsions, the most successful being molecules that combine a relatively long hydrophobic “tail” with a hydrophilic “head”:
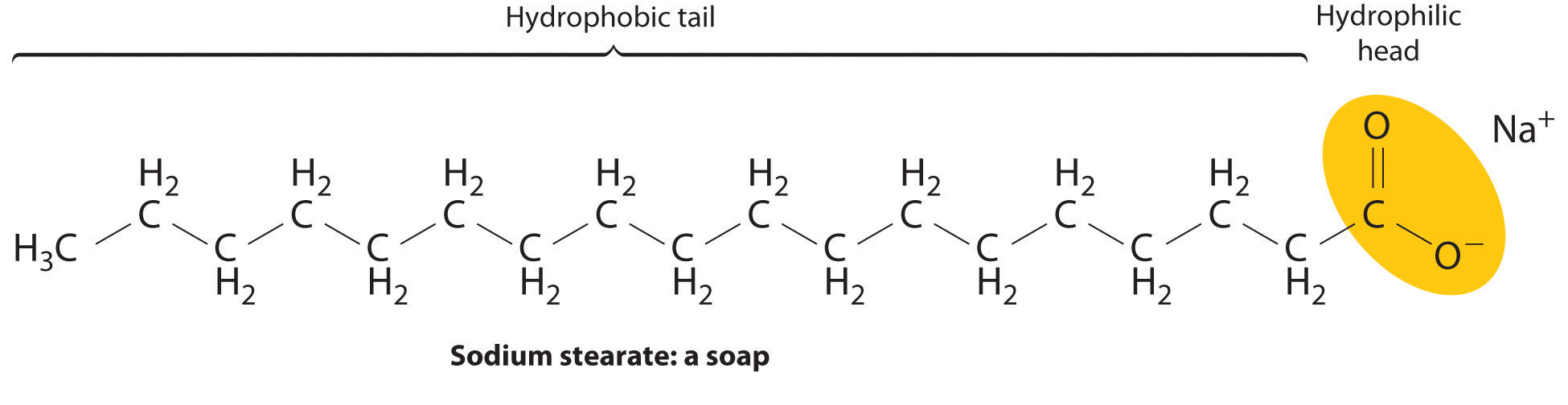
Examples of such emulsifying agents include soaps, which are salts of long-chain carboxylic acids, such as sodium stearate [CH3(CH2)16CO2−Na+], and detergents, such as sodium dodecyl sulfate [CH3(CH2)11OSO3−Na+], whose structures are as follows:
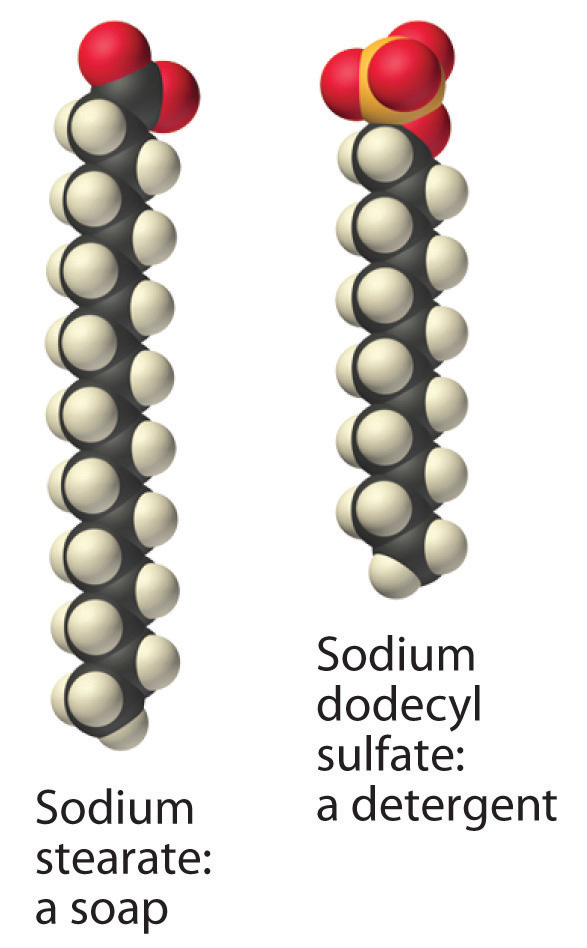
When you wash your laundry, the hydrophobic tails of soaps and detergents interact with hydrophobic particles of dirt or grease through dispersion forces, dissolving in the interior of the hydrophobic particle. The hydrophilic group is then exposed at the surface of the particle, which enables it to interact with water through ion–dipole forces and hydrogen bonding. This causes the particles of dirt or grease to disperse in the wash water and allows them to be removed by rinsing. Similar agents are used in the food industry to stabilize emulsions such as mayonnaise.
A related mechanism allows us to absorb and digest the fats in buttered popcorn and French fries. To solubilize the fats so that they can be absorbed, the gall bladder secretes a fluid called bile into the small intestine. Bile contains a variety of bile salts, detergent-like molecules that emulsify the fats.
Micelles
Detergents and soaps are surprisingly soluble in water in spite of their hydrophobic tails. The reason for their solubility is that they do not, in fact, form simple solutions. Instead, above a certain concentration they spontaneously form micellesA spherical or cylindrical aggregate of detergents or soaps in water that minimizes contact between the hydrophobic tails of the detergents or soaps and water., which are spherical or cylindrical aggregates that minimize contact between the hydrophobic tails and water. In a micelle, only the hydrophilic heads are in direct contact with water, and the hydrophobic tails are in the interior of the aggregate (part (a) in Figure 13.25 "Micelles and a Phospholipid Bilayer").
Figure 13.25 Micelles and a Phospholipid Bilayer
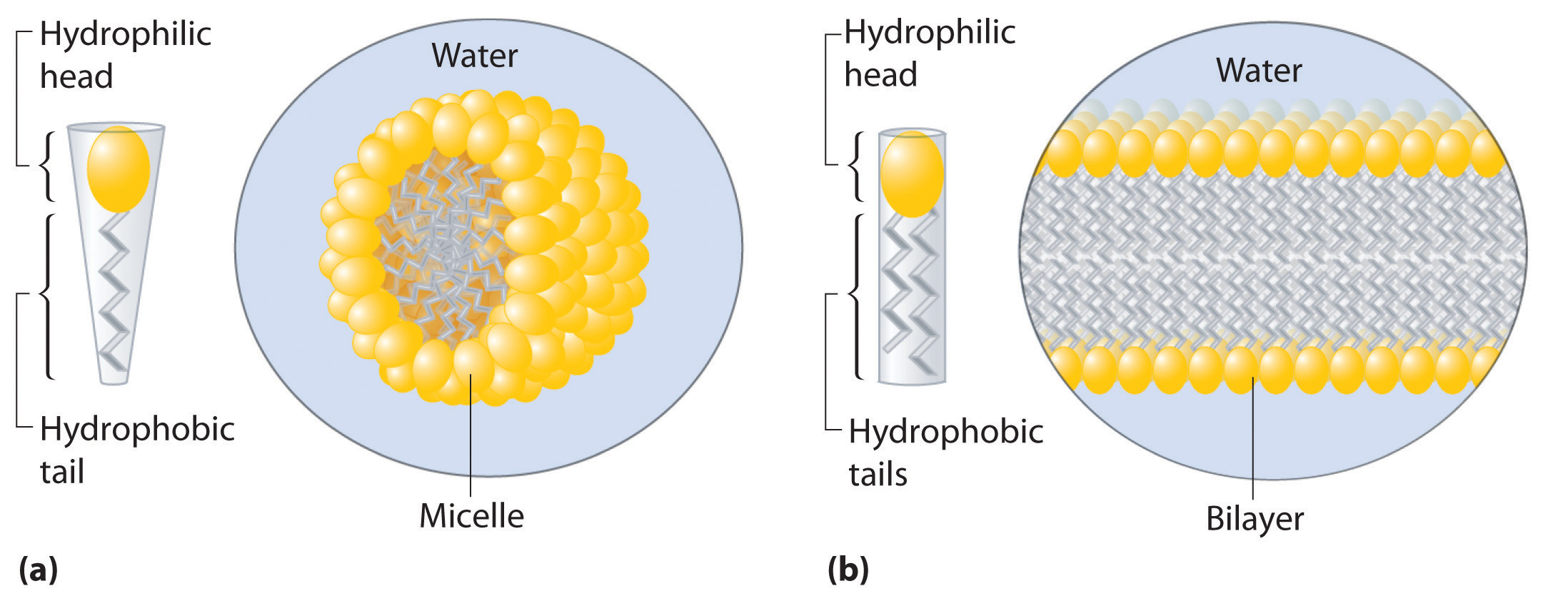
(a) Soaps and detergents, which contain a single hydrophobic tail on each molecule, form spherical micelles with the intertwined tails in the interior and the hydrophilic head groups on the exterior. (b) Phospholipids, which have two hydrophobic tails, tend to form extended double layers in which the hydrophobic tails are sandwiched between the hydrophilic head groups.
A large class of biological molecules called phospholipidsA large class of biological, detergent-like molecules that have a hydrophilic head and two hydrophobic tails and that form bilayers. consists of detergent-like molecules with a hydrophilic head and two hydrophobic tails, as can be seen in the molecule of phosphatidylcholine. The additional tail results in a cylindrical shape that prevents phospholipids from forming a spherical micelle. Consequently, phospholipids form bilayersA two-dimensional sheet consisting of a double layer of phospholipid molecules arranged tail to tail., extended sheets consisting of a double layer of molecules. As shown in part (b) in Figure 13.25 "Micelles and a Phospholipid Bilayer", the hydrophobic tails are in the center of the bilayer, where they are not in contact with water, and the hydrophilic heads are on the two surfaces, in contact with the surrounding aqueous solution.
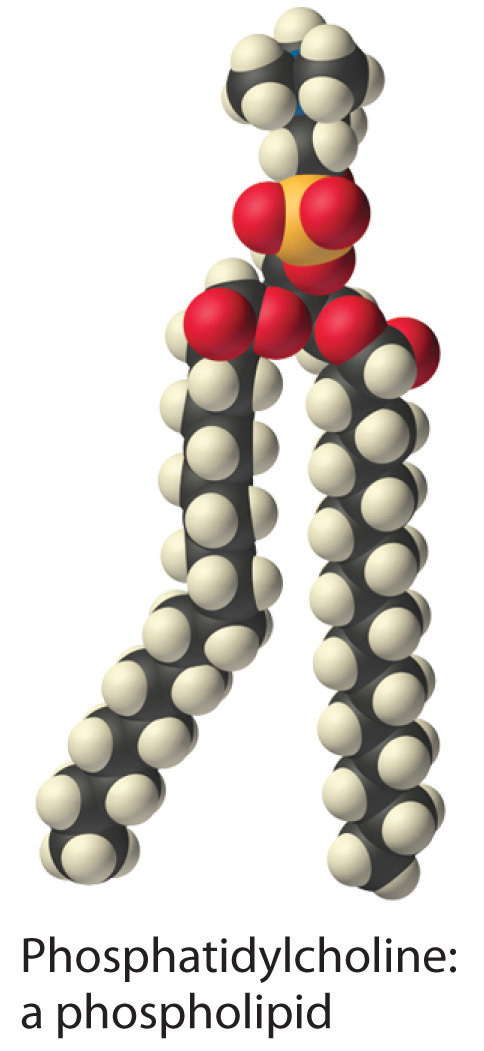
A cell membraneA mixture of phospholipids that form a phospholipid bilayer around the cell. is essentially a mixture of phospholipids that form a phospholipid bilayer. One definition of a cellA collection of molecules, capable of reproducing itself, that is surrounded by a phospholipid bilayer. is a collection of molecules surrounded by a phospholipid bilayer that is capable of reproducing itself. The simplest cells are bacteria, which consist of only a single compartment surrounded by a single membrane. Animal and plant cells are much more complex, however, and contain many different kinds of compartments, each surrounded by a membrane and able to carry out specialized tasks.
Summary
A suspension is a heterogeneous mixture of particles of one substance distributed throughout a second phase; the dispersed particles separate from the dispersing phase on standing. In contrast, the particles in a colloid are smaller and do not separate on standing. A colloid can be classified as a sol, a dispersion of solid particles in a liquid or solid; a gel, a semisolid sol in which all of the liquid phase has been absorbed by the solid particles; an aerosol, a dispersion of solid or liquid particles in a gas; or an emulsion, a dispersion of one liquid phase in another. A colloid can be distinguished from a true solution by its ability to scatter a beam of light, known as the Tyndall effect. Hydrophilic colloids contain an outer shell of groups that interact favorably with water, whereas hydrophobic colloids have an outer surface with little affinity for water. Emulsions are prepared by dispersing a hydrophobic liquid in water. In the absence of a dispersed hydrophobic liquid phase, solutions of detergents in water form organized spherical aggregates called micelles. Phospholipids are a class of detergent-like molecules that have two hydrophobic tails attached to a hydrophilic head. A bilayer is a two-dimensional sheet consisting of a double layer of phospholipid molecules arranged tail to tail with a hydrophobic interior and a hydrophilic exterior. Cells are collections of molecules that are surrounded by a phospholipid bilayer called a cell membrane and are able to reproduce themselves.
Key Takeaway
- Colloids and suspensions are mixtures whose properties are in many ways intermediate between those of true solutions and heterogeneous mixtures.
Conceptual Problems
-
How does a colloid differ from a suspension? Which has a greater effect on solvent properties, such as vapor pressure?
-
Is homogenized milk a colloid or a suspension? Is human plasma a colloid or a suspension? Justify your answers.
-
How would you separate the components of an emulsion of fat dispersed in an aqueous solution of sodium chloride?
13.7 End-of-Chapter Material
Application Problems
-
♦ Scuba divers utilize high-pressure gas in their tanks to allow them to breathe under water. At depths as shallow as 100 ft (30 m), the pressure exerted by water is 4.0 atm. At 25°C the values of Henry’s law constants for N2, O2, and He in blood are as follows: N2 = 6.5 × 10−4 mol/(L·atm), O2 = 1.28 × 10−3 mol/(L·atm), and He = 3.7 × 10−4 mol/(L·atm).
- What would be the concentration of nitrogen and oxygen in blood at sea level where the air is 21% oxygen and 79% nitrogen?
- What would be the concentration of nitrogen and oxygen in blood at a depth of 30 m, assuming that the diver is breathing compressed air?
-
♦ Many modern batteries take advantage of lithium ions dissolved in suitable electrolytes. Typical batteries have lithium concentrations of 0.10 M. Which aqueous solution has the higher concentration of ion pairs: 0.08 M LiCl or 1.4 M LiCl? Why? Does an increase in the number of ion pairs correspond to a higher or lower van’t Hoff factor? Batteries rely on a high concentration of unpaired Li+ ions. Why is using a more concentrated solution not an ideal strategy in this case?
-
Hydrogen sulfide, which is extremely toxic to humans, can be detected at a concentration of 2.0 ppb. At this level, headaches, dizziness, and nausea occur. At higher concentrations, however, the sense of smell is lost, and the lack of warning can result in coma and death can result. What is the concentration of H2S in milligrams per liter at the detection level? The lethal dose of hydrogen sulfide by inhalation for rats is 7.13 × 10−4 g/L. What is this lethal dose in ppm? The density of air is 1.2929 g/L.
-
One class of antibiotics consists of cyclic polyethers that can bind alkali metal cations in aqueous solution. Given the following antibiotics and cation selectivities, what conclusion can you draw regarding the relative sizes of the cavities?
Antibiotic Cation Selectivity nigericin K+ > Rb+ > Na+ > Cs+ > Li+ lasalocid Ba2+ >> Cs+ > Rb+, K+ > Na+, Ca2+, Mg2+ -
Phenylpropanolamine hydrochloride is a common nasal decongestant. An aqueous solution of phenylpropanolamine hydrochloride that is sold commercially as a children’s decongestant has a concentration of 6.67 × 10−3 M. If a common dose is 1.0 mL/12 lb of body weight, how many moles of the decongestant should be given to a 26 lb child?
-
The “freeze-thaw” method is often used to remove dissolved oxygen from solvents in the laboratory. In this technique, a liquid is placed in a flask that is then sealed to the atmosphere, the liquid is frozen, and the flask is evacuated to remove any gas and solvent vapor in the flask. The connection to the vacuum pump is closed, the liquid is warmed to room temperature and then refrozen, and the process is repeated. Why is this technique effective for degassing a solvent?
-
Suppose that, on a planet in a galaxy far, far away, a species has evolved whose biological processes require even more oxygen than we do. The partial pressure of oxygen on this planet, however, is much less than that on Earth. The chemical composition of the “blood” of this species is also different. Do you expect their “blood” to have a higher or lower value of the Henry’s law constant for oxygen at standard temperature and pressure? Justify your answer.
-
A car owner who had never taken general chemistry decided that he needed to put some ethylene glycol antifreeze in his car’s radiator. After reading the directions on the container, however, he decided that “more must be better.” Instead of using the recommended mixture (30% ethylene glycol/70% water), he decided to reverse the amounts and used a 70% ethylene glycol/30% water mixture instead. Serious engine problems developed. Why?
-
The ancient Greeks produced “Attic ware,” pottery with a characteristic black and red glaze. To separate smaller clay particles from larger ones, the powdered clay was suspended in water and allowed to settle. This process yielded clay fractions with coarse, medium, and fine particles, and one of these fractions was used for painting. Which size of clay particles forms a suspension, which forms a precipitate, and which forms a colloidal dispersion? Would the colloidal dispersion be better characterized as an emulsion? Why or why not? Which fraction of clay particles was used for painting?
-
The Tyndall effect is often observed in movie theaters, where it makes the beam of light from the projector clearly visible. What conclusions can you draw about the quality of the air in a movie theater where you observe a large Tyndall effect?
-
Aluminum sulfate is the active ingredient in styptic pencils, which can be used to stop bleeding from small cuts. The Al3+ ions induce aggregation of colloids in the blood, which facilitates formation of a blood clot. How can Al3+ ions induce aggregation of a colloid? What is the probable charge on the colloidal particles in blood?
-
♦ The liver secretes bile, which is essential for the digestion of fats. As discussed in Chapter 5 "Energy Changes in Chemical Reactions", fats are biomolecules with long hydrocarbon chains. The globules of fat released by partial digestion of food particles in the stomach and lower intestine are too large to be absorbed by the intestine unless they are emulsified by bile salts, such as glycocholate. Explain why a molecule like glycocholate is effective at creating an aqueous dispersion of fats in the digestive tract.
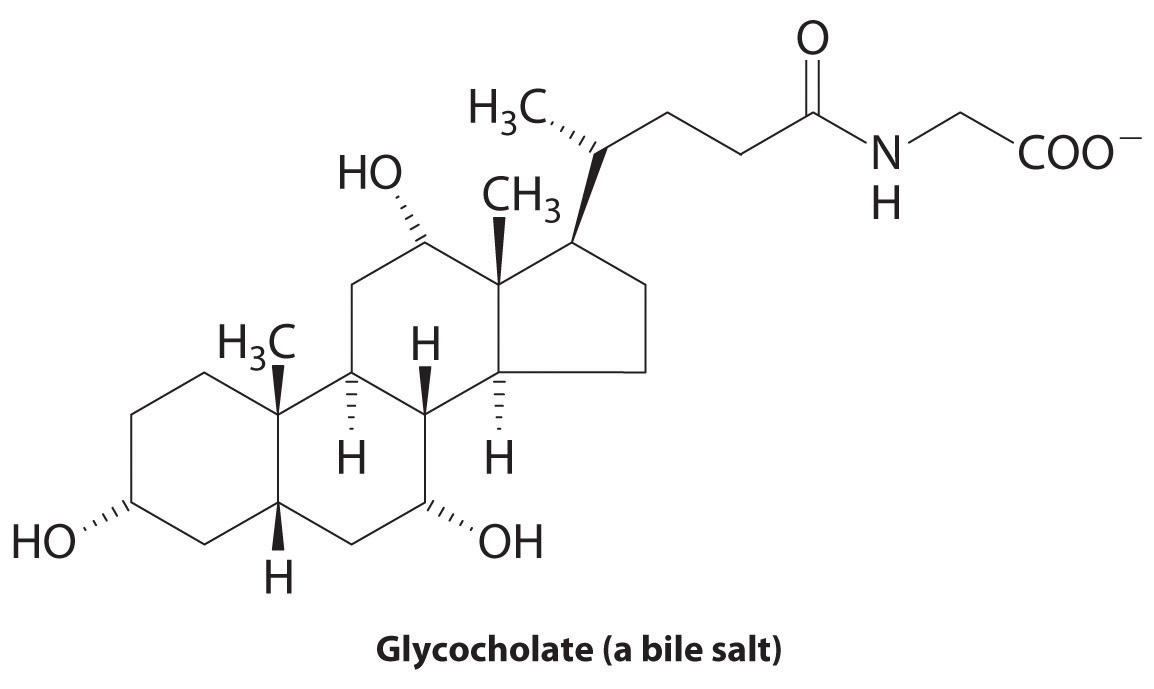
Problems marked with a ♦ involve multiple concepts.
Answers
-
- 1 atm: 2.7 × 10−4 M O2 and 5.1 × 10−4 M N2
- 4 atm: 1.1 × 10−3 M O2 and 2.1 × 10−3 M N2
-
-
2.6 × 10−6 mg/L, 550 ppm
-
-
1.4 × 10−5 mol
-
-
To obtain the same concentration of dissolved oxygen in their “blood” at a lower partial pressure of oxygen, the value of the Henry’s law constant would have to be higher.
-
-
The large, coarse particles would precipitate, the medium particles would form a suspension, and the fine ones would form a colloid. A colloid consists of solid particles in a liquid medium, so it is not an emulsion, which consists of small particles of one liquid suspended in another liquid. The finest particles would be used for painting.
-
-
-




