This is “Review and Practice”, section 18.3 from the book Economics Principles (v. 1.0). For details on it (including licensing), click here.

For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.

Has this book helped you? Consider passing it on:
Help Creative Commons
Creative Commons supports free culture from music to education. Their licenses helped make this book available to you.
Help a Public School
DonorsChoose.org helps people like you help teachers fund their classroom projects, from art supplies to books to calculators.

18.3 Review and Practice

Summary

Pollution is a by-product of human activity. It occurs when the environment becomes scarce—when dumping garbage imposes a cost. There are benefits as well as costs to pollution; the efficient quantity of pollution occurs where the difference between total benefits and total costs is maximized. This solution is achieved where the marginal benefit of additional pollution equals the marginal cost. We have seen that an alternative approach shows that efficiency is also achieved where the marginal benefit of pollution abatement equals the marginal cost of abatement.

Economists measure the benefits of pollution in terms of the costs of not dumping the pollution. The same curve can be read from left to right as the marginal benefit curve for emissions and from right to left as the marginal cost curve for abatement.

The costs of pollution are measured in two ways. One is through direct surveys. Respondents can be asked how much compensation they would be willing to accept in exchange for a reduction in environmental pollution; alternatively, they can be asked how much they would pay for an improvement in environmental quality. A second approach infers the marginal cost of increased pollution from other relationships. The effects of pollution on house prices or rental values, for example, allow economists to estimate the value people place on environmental quality. Pollution costs can also be estimated on the basis of the costs they impose on firms in production.

Three types of policies are available to reduce pollution. Moral suasion is sometimes used, but it is effective only under limited conditions. Command-and-control regulation is used most commonly, but it is likely to be inefficient. It also fails to provide incentives for technological change in the long run. The most promising policies are the incentive approaches, which include emissions taxes and marketable pollution permits. Both can be designed to reduce emissions at the lowest cost possible, and both create an incentive for firms to search out new and cheaper ways to reduce emissions.

Although public policy has stressed command-and-control methods in the past, pollution rights exchanges are now being introduced. Past policies may have been inefficient, but they have succeeded in improving air quality, at least in the nation’s cities.

Concept Problems

  1. We have noted that economists consider the benefits and costs of pollution from the perspective of people’s preferences. Some critics argue, however, that the interests of plants and animals should be considered: for example, if pollution is harming trees, the trees have a right to protection. Do you think that is a good idea? How would it be implemented?
  2. List five choices you make that result in pollution. What price do you pay to pollute the environment? Does that price affect your choices?
  3. In any urban area, what group is likely to be exposed to a greater level of pollution—rich people or poor people? (Hint: Utilize the findings of economists concerning the relationship between house prices and pollution levels.)
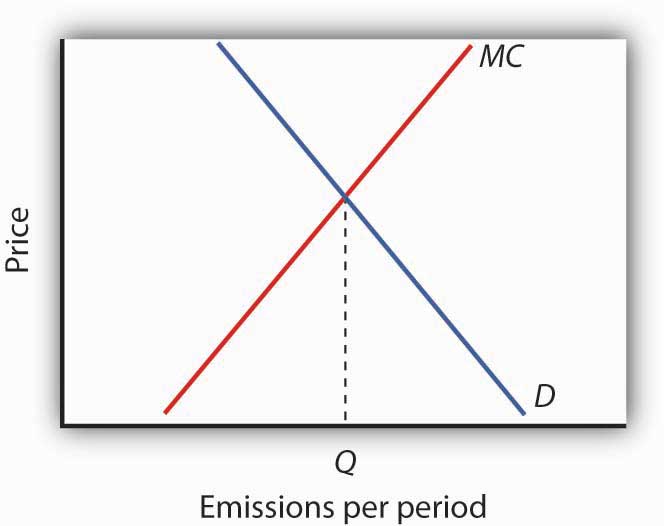
  4. Suppose the accompanying graph shows the demand and marginal cost curves, D and MC, for a pollutant in a particular area. How do you think future economic and population growth will affect the efficient rate of emissions per period, Q, and thus the level of pollution?

Figure 18.9

  1. “Environmental quality is not just a matter of technical efficiency; it’s about how people relate to nature. Economists are completely off base in their analysis of the benefits and costs of pollution.” What is your opinion of this quote?
  2. Campaigns that exhort us to “Give a hoot—don’t pollute” imply that anyone who pollutes the environment is uncaring—that people who are concerned about environmental quality would not be dumping garbage into the environment. Is that true?
  3. We have seen that a system of marketable pollution permits achieves the same solution as a system of emissions taxes. Which do you think would be fairer? Why?
  4. Many environmentalists are horrified by the notion of marketable pollution permits advocated by economists. These environmentalists insist that pollution is wrong, and that no one should be able to buy the right to pollute the environment. What do you think?
  5. Some people object that charging firms for their emissions will do no good—firms will simply raise their prices and go on doing what they were doing before. Comment on this objection to emissions taxes.
  6. Suppose firms in a perfectly competitive industry generate water pollution as a by-product of their production, and they are not charged for this. Who benefits from their use of the environment as a dumping ground? If an emissions tax is imposed, costs to these firms increase and emissions drop. Who will bear the burden of this tax? Is that fair?
  7. The Case in Point on measurement suggested that the demand curve for locating a house farther from a hazardous waste site could be inferred from property value studies. Explain how this could be the case.
  8. Does the road pricing system in Singapore strike you as fair? Would you like to see such a system in your own area? Why or why not?

Numerical Problems

  1. Suppose the dry-cleaning industry is perfectly competitive. The process of dry cleaning generates emissions that pollute the air, and firms now emit this pollution at no cost. Suppose that the long run equilibrium price for dry cleaning a typical item is $5, and a pollution-control program increases the marginal cost by $1 per item.

    1. How will the pollution-control program affect the price of dry-cleaning services in the short run? Explain and illustrate graphically.
    2. Explain and illustrate graphically how the program will affect the output of dry-cleaning services in the short run.
    3. Explain and illustrate graphically how the $1 increase in cost will affect the price of dry-cleaning services in the long run.
    4. Explain and illustrate graphically how the cost increase will affect the quantity of dry-cleaning services produced in the long run.
    5. Who pays for pollution control in the industry? Explain, relating your answer to the basic conclusion about long-run equilibrium in a perfectly competitive industry.

  2. Now suppose the dry-cleaning industry in the community is monopolistically competitive. Suppose the initial price per unit of dry-cleaning is $6. Suppose that a charge levied on dry-cleaning firms for the pollution they generate increases the cost of a unit of dry-cleaning by $1.

    1. Explain and illustrate graphically how the $1 charge will affect the price charged by typical firm in the short run.
    2. Explain and illustrate graphically how the $1 charge will affect the typical firm’s output in the short run.
    3. Now explain and illustrate graphically how the $1 charge will affect price and output of a typical firm in the long run. Through what mechanism does this occur?
    4. Compare your answers for a world of monopolistically competitive firms to a world of perfectly competitive firms. Is there any significant difference between the conclusions of the two models?

  3. Suppose local government regulations allow only a single firm to provide dry-cleaning services to a local community, and this firm generates pollution as in Problem 1. The firm initially charges a price of $4 per item. Now a pollution-control program is imposed, increasing the firm’s marginal and average total costs by $1 per item.

    1. Explain and illustrate graphically how the program will affect the firm’s price and output.
    2. Who pays for the pollution-control program?

  4. Suppose the marginal benefit (MB) and marginal cost (MC) curves for emitting particulate matter are given by the following schedules, where E is the quantity of emissions per period. The marginal benefits and costs are measured at the quantities of emissions shown.

    E/period MB MC
    0 $230 $0
    200 190 10
    400 150 30
    600 110 50
    800 70 70
    1,000 30 90
    1. Plot the marginal benefit and marginal cost curves and state the efficient quantity of emissions per period.
    2. What quantity of emissions will occur when the price of emissions is zero?
    3. What tax rate would achieve the efficient rate of emissions?

  5. Now suppose that rising incomes increase marginal cost as follows:

    E/period New MC
    0 $0
    200 30
    400 70
    600 110
    800 150
    1,000 190
    1. Plot the new marginal cost curve in the graph you drew in Problem 4. What is the new efficient quantity of emissions per period?
    2. What quantity of emissions will occur when the price of emissions is zero?
    3. What tax rate would achieve the efficient rate of emissions?
  6. The text contains the following statement: “All other variables unchanged, increasing the distance from a house to a hazardous site by 10% increased house value by 0.3%.” What is the price elasticity of house prices with respect to proximity to a hazardous waste site?