This is “Expressing Numbers”, section 2.1 from the book Beginning Chemistry (v. 1.0). For details on it (including licensing), click here.

For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.

Has this book helped you? Consider passing it on:
Help Creative Commons
Creative Commons supports free culture from music to education. Their licenses helped make this book available to you.
Help a Public School
DonorsChoose.org helps people like you help teachers fund their classroom projects, from art supplies to books to calculators.

2.1 Expressing Numbers

Learning Objective

  1. Learn to express numbers properly.

Quantities have two parts: the number and the unit. The number tells “how many.” It is important to be able to express numbers properly so that the quantities can be communicated properly.

Standard notationA straightforward expression of a number. is the straightforward expression of a number. Numbers such as 17, 101.5, and 0.00446 are expressed in standard notation. For relatively small numbers, standard notation is fine. However, for very large numbers, such as 306,000,000, or for very small numbers, such as 0.000000419, standard notation can be cumbersome because of the number of zeros needed to place nonzero numbers in the proper position.

Scientific notationAn expression of a number using powers of 10. is an expression of a number using powers of 10. Powers of 10 are used to express numbers that have many zeros:

100 = 1
101 = 10
102 = 100 = 10 × 10
103 = 1,000 = 10 × 10 × 10
104 = 10,000 = 10 × 10 × 10 × 10

and so forth. The raised number to the right of the 10 indicating the number of factors of 10 in the original number is the exponentThe raised number to the right of a 10 indicating the number of factors of 10 in the original number.. (Scientific notation is sometimes called exponential notation.) The exponent’s value is equal to the number of zeros in the number expressed in standard notation.

Small numbers can also be expressed in scientific notation but with negative exponents:

10−1 = 0.1 = 1/10
10−2 = 0.01 = 1/100
10−3 = 0.001 = 1/1,000
10−4 = 0.0001 = 1/10,000

and so forth. Again, the value of the exponent is equal to the number of zeros in the denominator of the associated fraction. A negative exponent implies a decimal number less than one.

A number is expressed in scientific notation by writing the first nonzero digit, then a decimal point, and then the rest of the digits. The part of a number in scientific notation that is multiplied by a power of 10 is called the coefficientThe part of a number in scientific notation that is multiplied by a power of 10.. Then determine the power of 10 needed to make that number into the original number and multiply the written number by the proper power of 10. For example, to write 79,345 in scientific notation,

79,345 = 7.9345 × 10,000 = 7.9345 × 104

Thus, the number in scientific notation is 7.9345 × 104. For small numbers, the same process is used, but the exponent for the power of 10 is negative:

0.000411 = 4.11 × 1/10,000 = 4.11 × 10−4

Typically, the extra zero digits at the end or the beginning of a number are not included. (See Figure 2.1 "Using Scientific Notation".)

Figure 2.1 Using Scientific Notation

The earth is about 93,000,000 miles from the sun. In scientific notation, this is 9.3 × 107 miles.

© Thinkstock

Example 1

Express these numbers in scientific notation.

  1. 306,000
  2. 0.00884
  3. 2,760,000
  4. 0.000000559

Solution

  1. The number 306,000 is 3.06 times 100,000, or 3.06 times 105. In scientific notation, the number is 3.06 × 105.
  2. The number 0.00884 is 8.84 times 1/1,000, which is 8.84 times 10−3. In scientific notation, the number is 8.84 × 10−3.
  3. The number 2,760,000 is 2.76 times 1,000,000, which is the same as 2.76 times 106. In scientific notation, the number is written as 2.76 × 106. Note that we omit the zeros at the end of the original number.
  4. The number 0.000000559 is 5.59 times 1/10,000,000, which is 5.59 times 10−7. In scientific notation, the number is written as 5.59 × 10−7.

Test Yourself

Express these numbers in scientific notation.

  1. 23,070
  2. 0.0009706

Answers

  1. 2.307 × 104
  2. 9.706 × 10−4

Another way to determine the power of 10 in scientific notation is to count the number of places you need to move the decimal point to get a numerical value between 1 and 10. The number of places equals the power of 10. This number is positive if you move the decimal point to the right and negative if you move the decimal point to the left:

56↖4,9↖30↖20↖1=5.69 × 1040.0↗10↗20↗30↗42↗58=2.8 × 10−5 

Many quantities in chemistry are expressed in scientific notation. When performing calculations, you may have to enter a number in scientific notation into a calculator. Be sure you know how to correctly enter a number in scientific notation into your calculator. Different models of calculators require different actions for properly entering scientific notation. If in doubt, consult your instructor immediately. (See Figure 2.2 "Scientific Notation on a Calculator".)

Figure 2.2 Scientific Notation on a Calculator

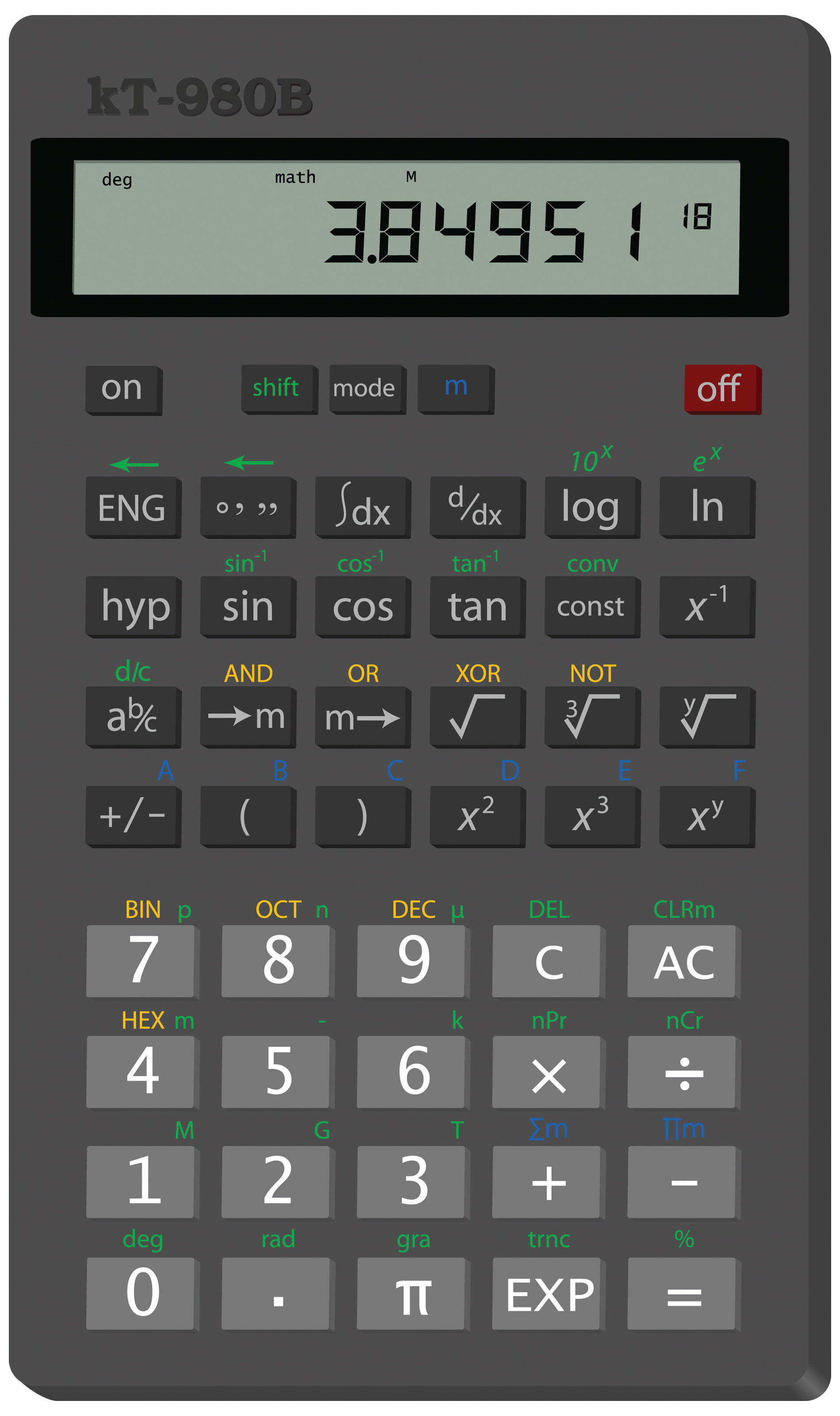
This calculator shows only the coefficient and the power of 10 to represent the number in scientific notation. Thus, the number being displayed is 3.84951 × 1018, or 3,849,510,000,000,000,000.

© Thinkstock

Key Takeaways

  • Standard notation expresses a number normally.
  • Scientific notation expresses a number as a coefficient times a power of 10.
  • The power of 10 is positive for numbers greater than 1 and negative for numbers between 0 and 1.

Exercises

  1. Express these numbers in scientific notation.

    1. 56.9
    2. 563,100
    3. 0.0804
    4. 0.00000667

  2. Express these numbers in scientific notation.

    1. −890,000
    2. 602,000,000,000
    3. 0.0000004099
    4. 0.000000000000011

  3. Express these numbers in scientific notation.

    1. 0.00656
    2. 65,600
    3. 4,567,000
    4. 0.000005507

  4. Express these numbers in scientific notation.

    1. 65
    2. −321.09
    3. 0.000077099
    4. 0.000000000218

  5. Express these numbers in standard notation.

    1. 1.381 × 105
    2. 5.22 × 10−7
    3. 9.998 × 104

  6. Express these numbers in standard notation.

    1. 7.11 × 10−2
    2. 9.18 × 102
    3. 3.09 × 10−10

  7. Express these numbers in standard notation.

    1. 8.09 × 100
    2. 3.088 × 10−5
    3. −4.239 × 102

  8. Express these numbers in standard notation.

    1. 2.87 × 10−8
    2. 1.78 × 1011
    3. 1.381 × 10−23

  9. These numbers are not written in proper scientific notation. Rewrite them so that they are in proper scientific notation.

    1. 72.44 × 103
    2. 9,943 × 10−5
    3. 588,399 × 102

  10. These numbers are not written in proper scientific notation. Rewrite them so that they are in proper scientific notation.

    1. 0.000077 × 10−7
    2. 0.000111 × 108
    3. 602,000 × 1018

  11. These numbers are not written in proper scientific notation. Rewrite them so that they are in proper scientific notation.

    1. 345.1 × 102
    2. 0.234 × 10−3
    3. 1,800 × 10−2

  12. These numbers are not written in proper scientific notation. Rewrite them so that they are in proper scientific notation.

    1. 8,099 × 10−8
    2. 34.5 × 100
    3. 0.000332 × 104

  13. Write these numbers in scientific notation by counting the number of places the decimal point is moved.

    1. 123,456.78
    2. 98,490
    3. 0.000000445

  14. Write these numbers in scientific notation by counting the number of places the decimal point is moved.

    1. 0.000552
    2. 1,987
    3. 0.00000000887

  15. Use your calculator to evaluate these expressions. Express the final answer in proper scientific notation.

    1. 456 × (7.4 × 108) = ?
    2. (3.02 × 105) ÷ (9.04 × 1015) = ?
    3. 0.0044 × 0.000833 = ?

  16. Use your calculator to evaluate these expressions. Express the final answer in proper scientific notation.

    1. 98,000 × 23,000 = ?
    2. 98,000 ÷ 23,000 = ?
    3. (4.6 × 10−5) × (2.09 × 103) = ?

  17. Use your calculator to evaluate these expressions. Express the final answer in proper scientific notation.

    1. 45 × 132 ÷ 882 = ?
    2. [(6.37 × 104) × (8.44 × 10−4)] ÷ (3.2209 × 1015) = ?

  18. Use your calculator to evaluate these expressions. Express the final answer in proper scientific notation.

    1. (9.09 × 108) ÷ [(6.33 × 109) × (4.066 × 10−7)] = ?
    2. 9,345 × 34.866 ÷ 0.00665 = ?

Answers

    1. 5.69 × 101
    2. 5.631 × 105
    3. 8.04 × 10−2
    4. 6.67 × 10−6

    1. 6.56 × 10−3
    2. 6.56 × 104
    3. 4.567 × 106
    4. 5.507 × 10−6

    1. 138,100
    2. 0.000000522
    3. 99,980

    1. 8.09
    2. 0.00003088
    3. −423.9

    1. 7.244 × 104
    2. 9.943 × 10−2
    3. 5.88399 × 107

    1. 3.451 × 104
    2. 2.34 × 10−4
    3. 1.8 × 101

    1. 1.2345678 × 105
    2. 9.849 × 104
    3. 4.45 × 10−7

    1. 3.3744 × 1011
    2. 3.3407 × 10−11
    3. 3.665 × 10−6

    1. 6.7346 × 100
    2. 1.6691 × 10−14