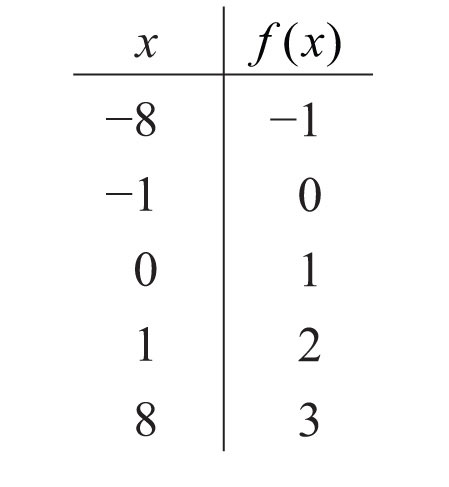This is “Simplifying Radical Expressions”, section 8.2 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
8.2 Simplifying Radical Expressions
Learning Objectives
- Simplify radical expressions using the product and quotient rule for radicals.
- Use formulas involving radicals.
- Evaluate given square root and cube root functions.
Simplifying Radical Expressions
An algebraic expression that contains radicals is called a radical expressionAn algebraic expression that contains radicals.. We use the product and quotient rules to simplify them.
Example 1: Simplify: .
Solution: Use the fact that when n is odd.

Answer:
Example 2: Simplify: .
Solution: The square root has index 2; use the fact that when n is even.

Since x is a variable, it may represent a negative number. Thus we need to ensure that the result is positive by including the absolute value operator.
Answer:
Important Note
Typically, at this point beginning algebra texts note that all variables are assumed to be positive. If this is the case, then x in the previous example is positive and the absolute value operator is not needed. The example can be simplified as follows:
In this section, we will assume that all variables are positive. This allows us to focus on calculating nth roots without the technicalities associated with the principal nth root problem. For this reason, we will use the following property for the rest of the section:
When simplifying radical expressions, look for factors with powers that match the index.
Example 3: Simplify: .
Solution: Begin by determining the square factors of 18, , and .
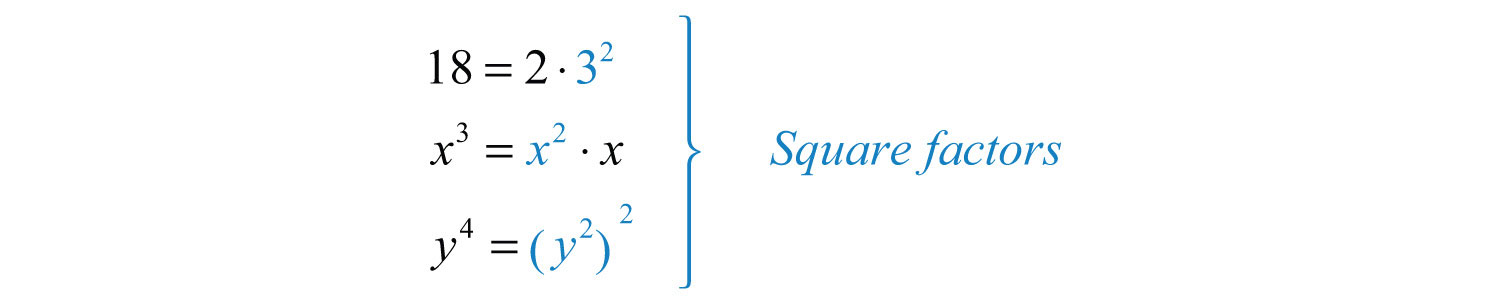
Make these substitutions and then apply the product rule for radicals and simplify.
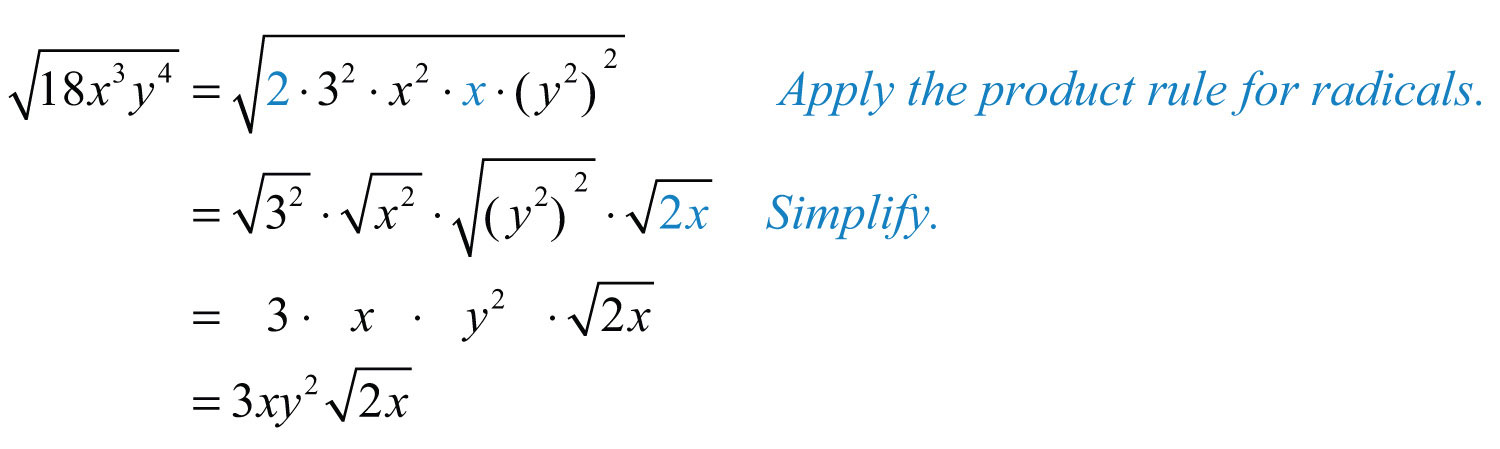
Answer:
Example 4: Simplify: .
Solution: Begin by determining the square factors of 4, , and .
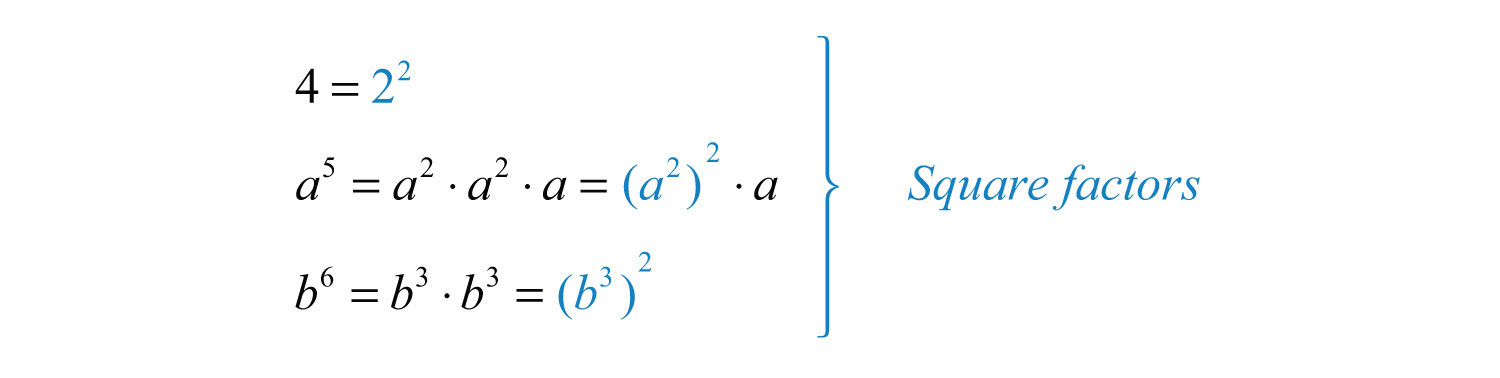
Make these substitutions and then apply the product rule for radicals and simplify.

Answer:
Example 5: Simplify: .
Solution: Begin by determining the cubic factors of 80, , and .
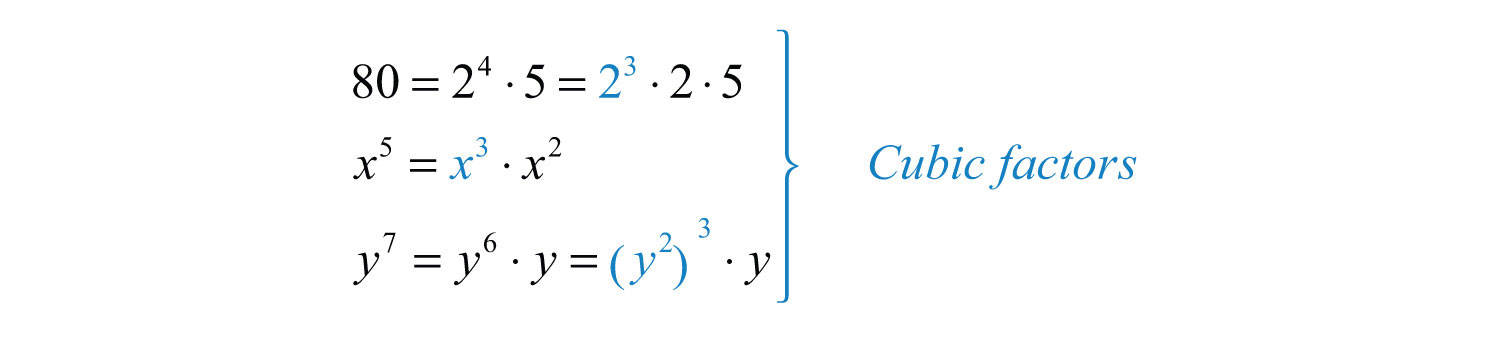
Make these substitutions and then apply the product rule for radicals and simplify.
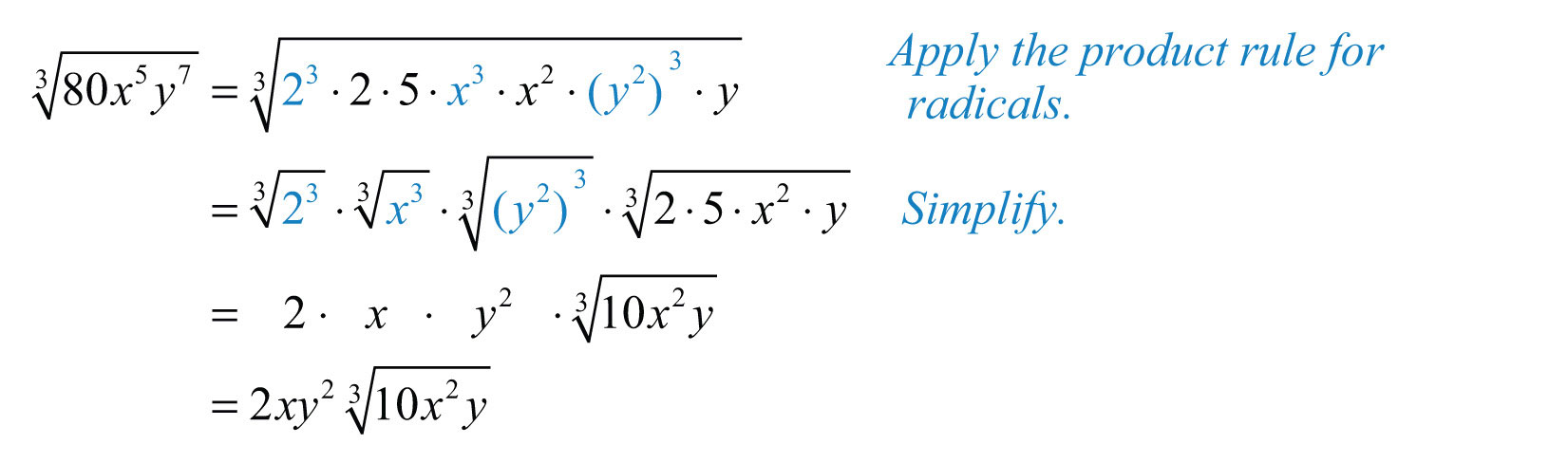
Answer:
Example 6: Simplify .
Solution: The coefficient and thus does not have any perfect cube factors. It will be left as the only remaining radicand because all of the other factors are cubes, as illustrated below:
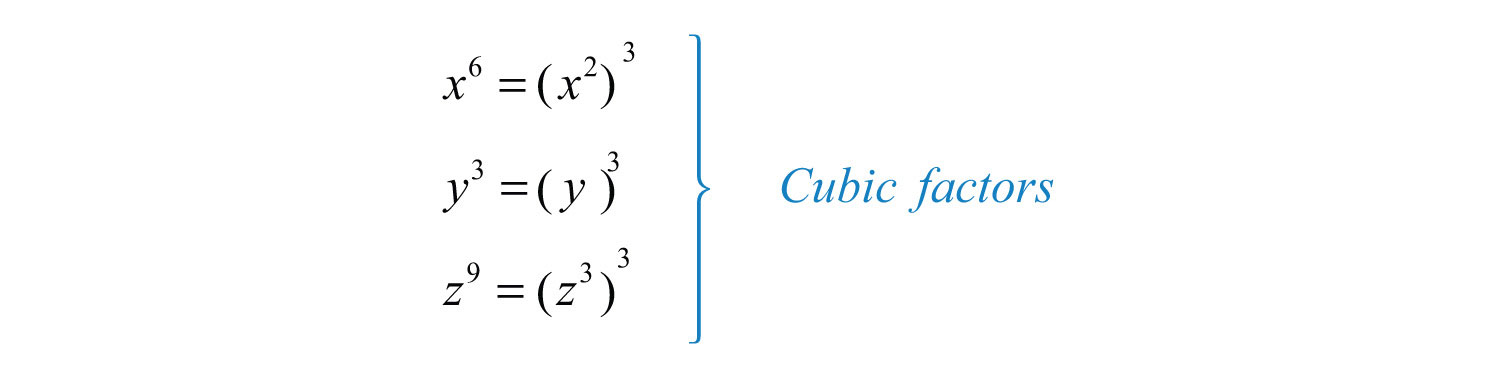
Replace the variables with these equivalents, apply the product and quotient rule for radicals, and then simplify.
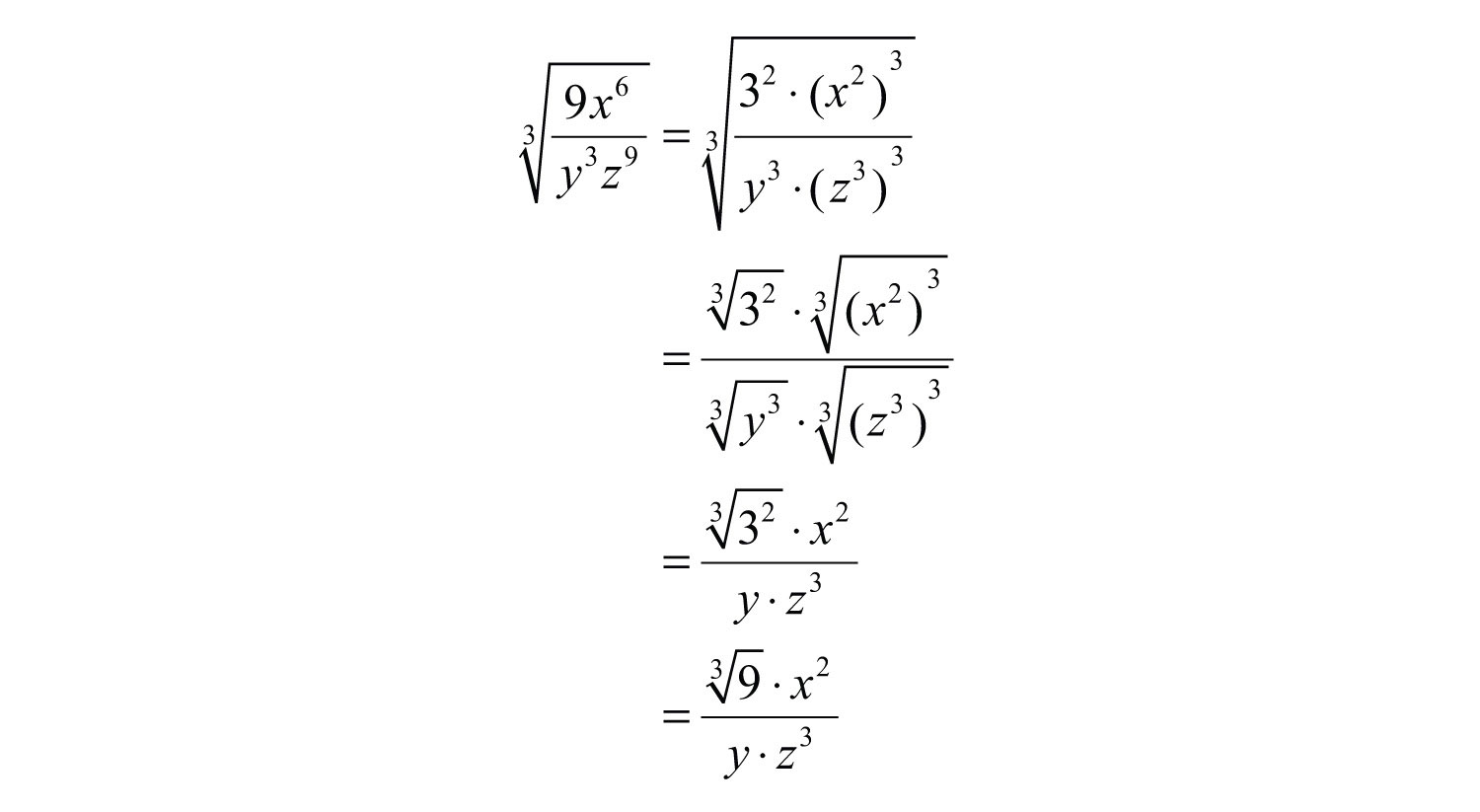
Answer:
Example 7: Simplify: .
Solution: Determine all factors that can be written as perfect powers of 4. Here it is important to see that . Hence the factor will be left inside the radical.
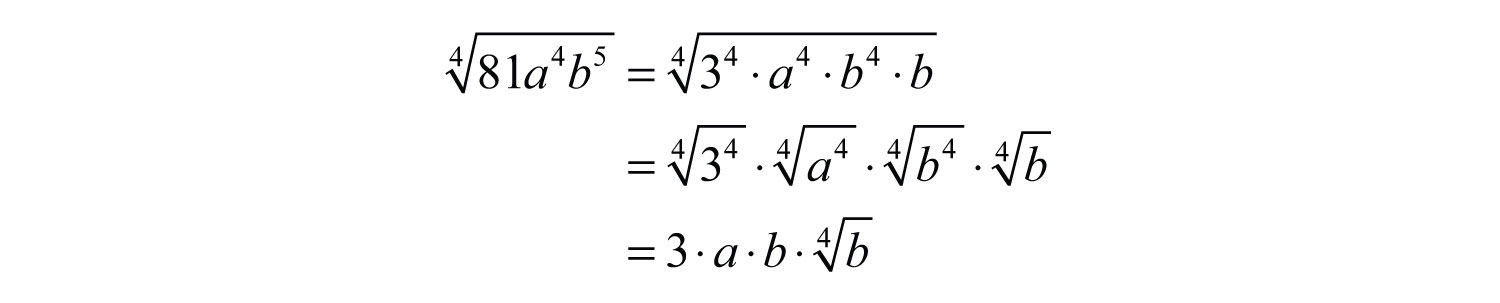
Answer:
Example 8: Simplify: .
Solution: Notice that the variable factor x cannot be written as a power of 5 and thus will be left inside the radical. In addition, for ; the factor y will be left inside the radical as well.
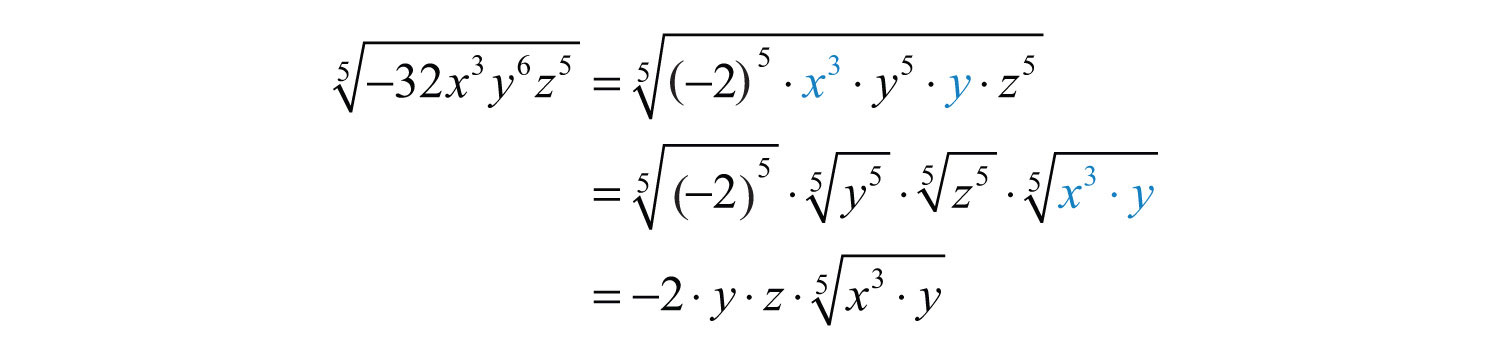
Answer:
Try this! Simplify: . (Assume all variables are positive.)
Answer:
Video Solution
(click to see video)Tip
To easily simplify an nth root, we can divide the powers by the index.
If the index does not divide into the power evenly, then we can use the quotient and remainder to simplify. For example,
The quotient is the exponent of the factor outside of the radical, and the remainder is the exponent of the factor left inside the radical.
Formulas Involving Radicals
We next review the distance formula. Given two points and ,
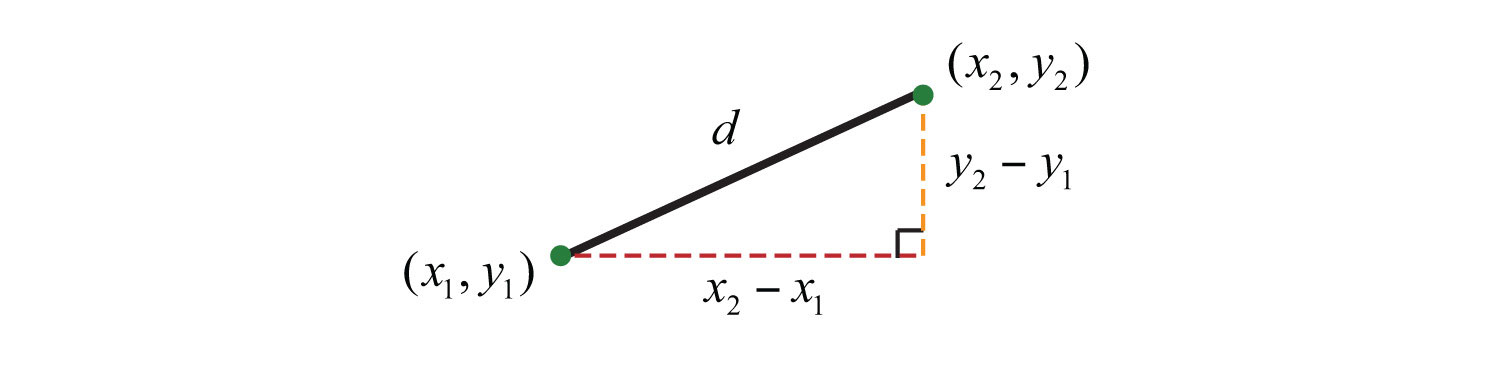
The distance, d, between them is given by the following formula:
Distance formulaGiven two points and calculate the distance d between them using the formula d = : |
Recall that this formula was derived from the Pythagorean theorem.
Example 9: Calculate the distance between (−4, 7) and (2, 1).
Solution: Use the distance formula with the following points.
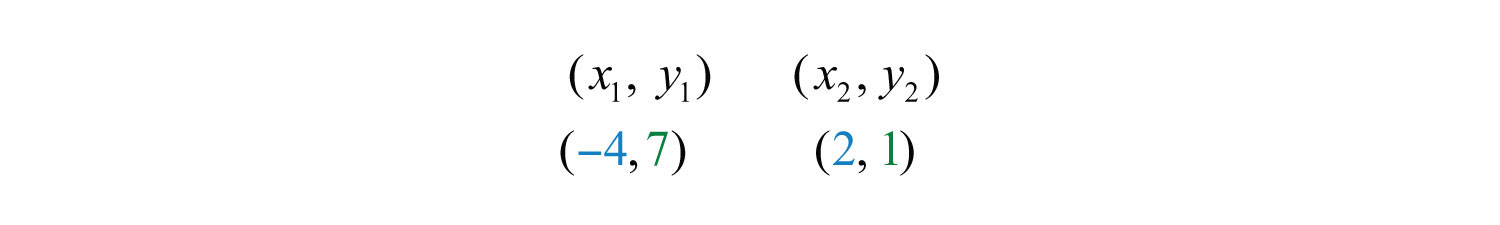
It is a good practice to include the formula in its general form before substituting values for the variables; this improves readability and reduces the probability of making errors.
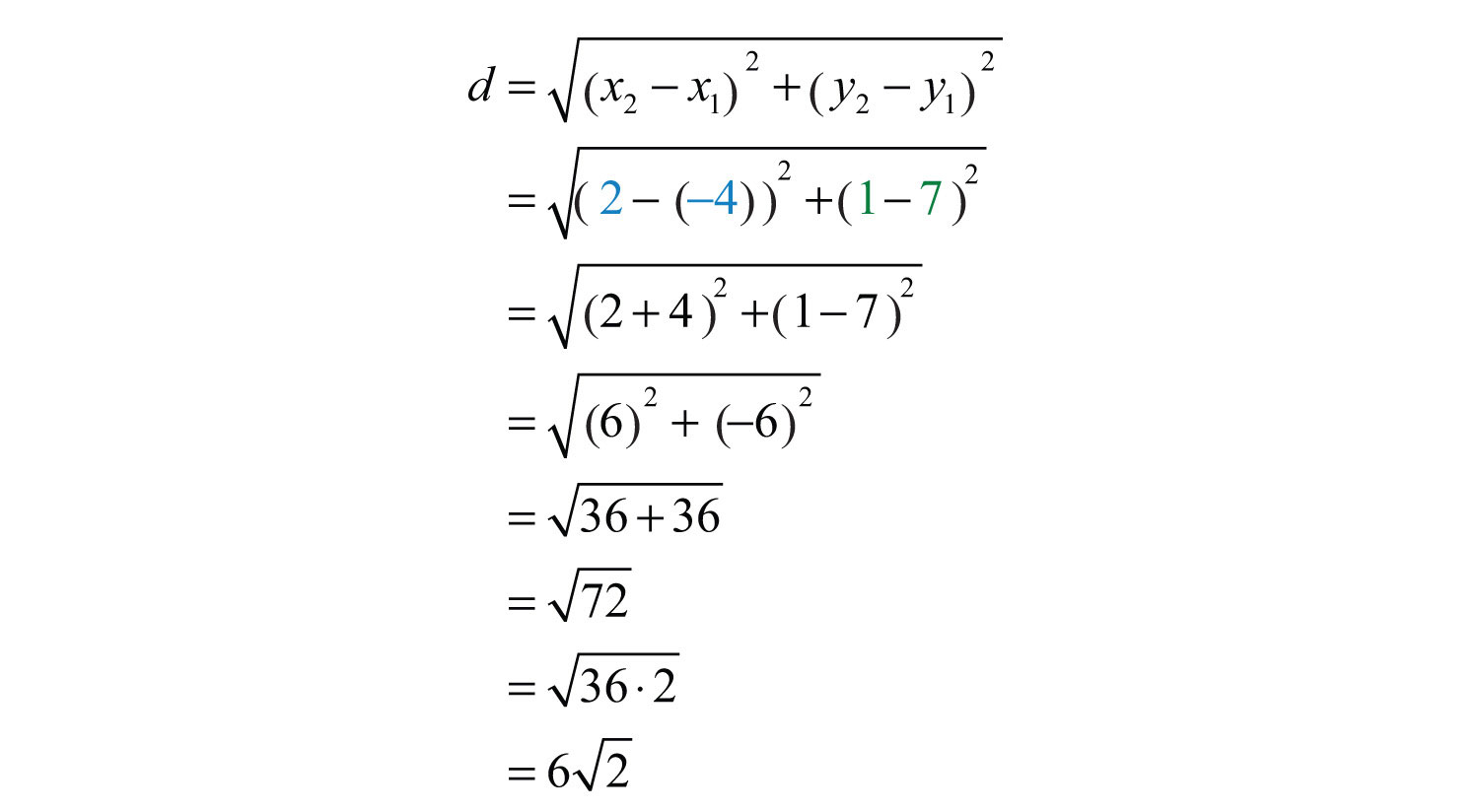
Answer: units
Example 10: The period, T, of a pendulum in seconds is given by the formula
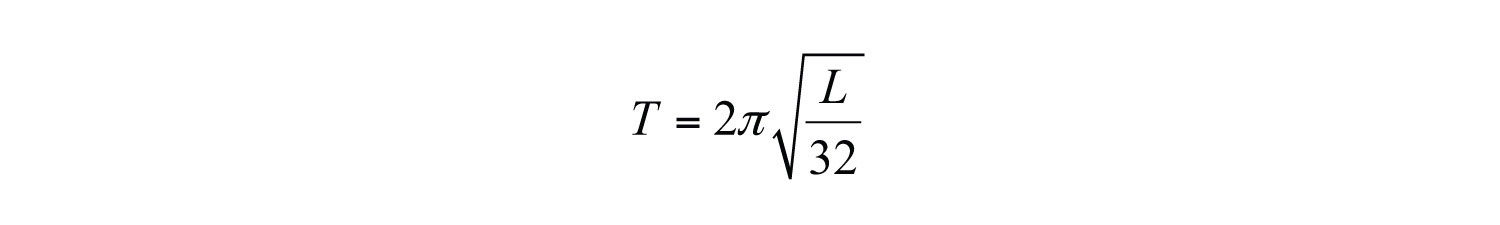
where L represents the length of the pendulum in feet. If the length of a pendulum measures 6 feet, then calculate the period rounded off to the nearest tenth of a second.
Solution: Substitute 6 for L and then simplify.

Answer: The period is approximately 2.7 seconds.
Square Root and Cube Root Functions
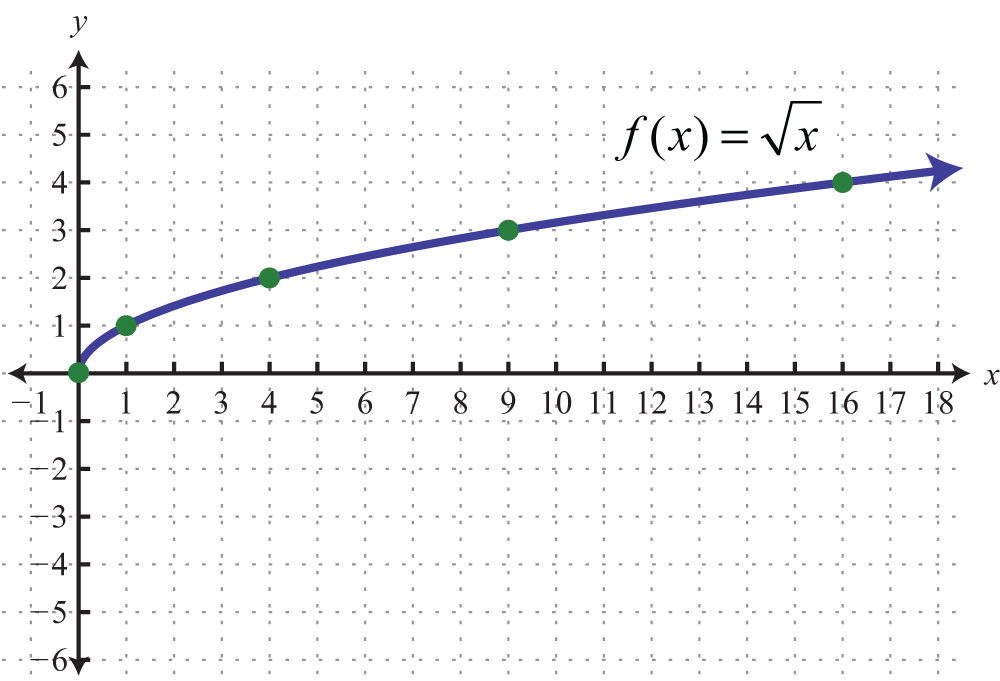
We begin with the square root functionThe function .:
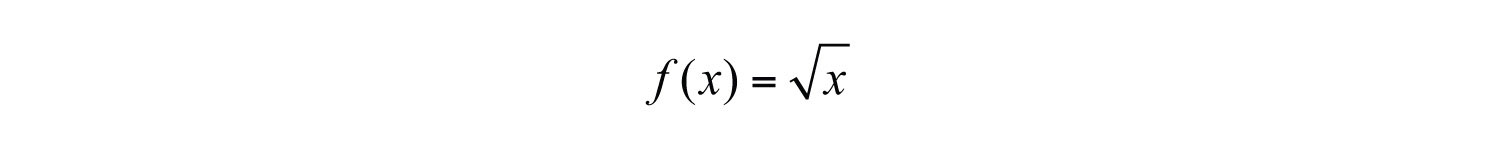
We know that the square root is not a real number when the radicand x is negative. Therefore, we conclude that the domain consists of all real numbers greater than or equal to 0. Here we choose 0 and some positive values for x, calculate the corresponding y-values, and plot the resulting ordered pairs.
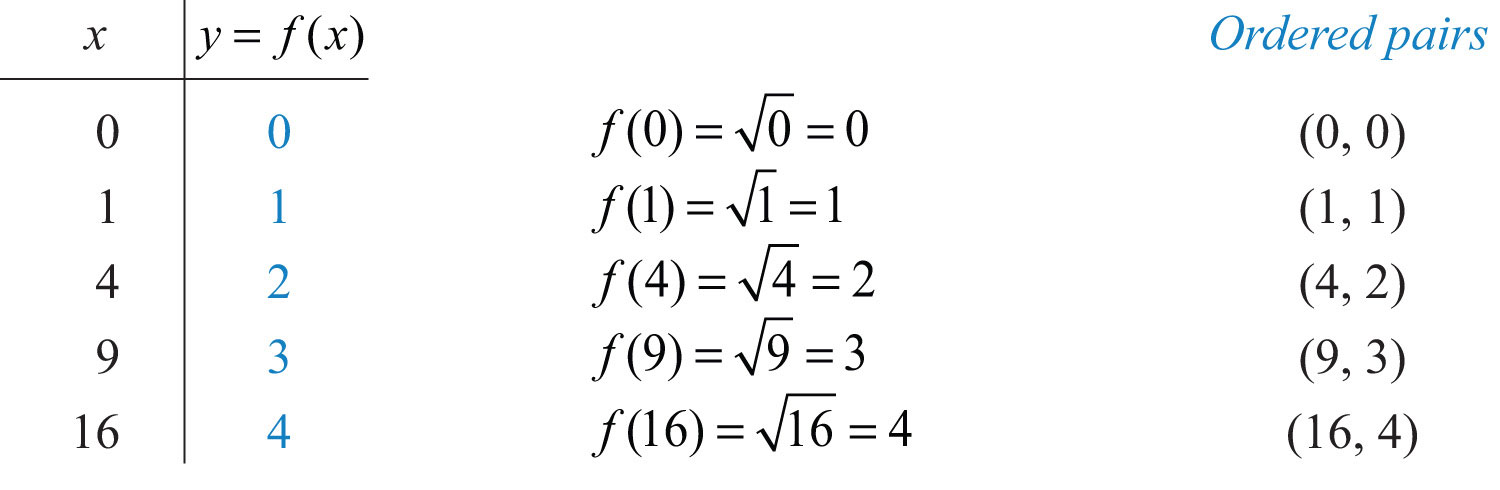
After plotting the points, we can then sketch the graph of the square root function.
Example 11: Given the function , find , , and .
Solution: Replace x with each of the given values.
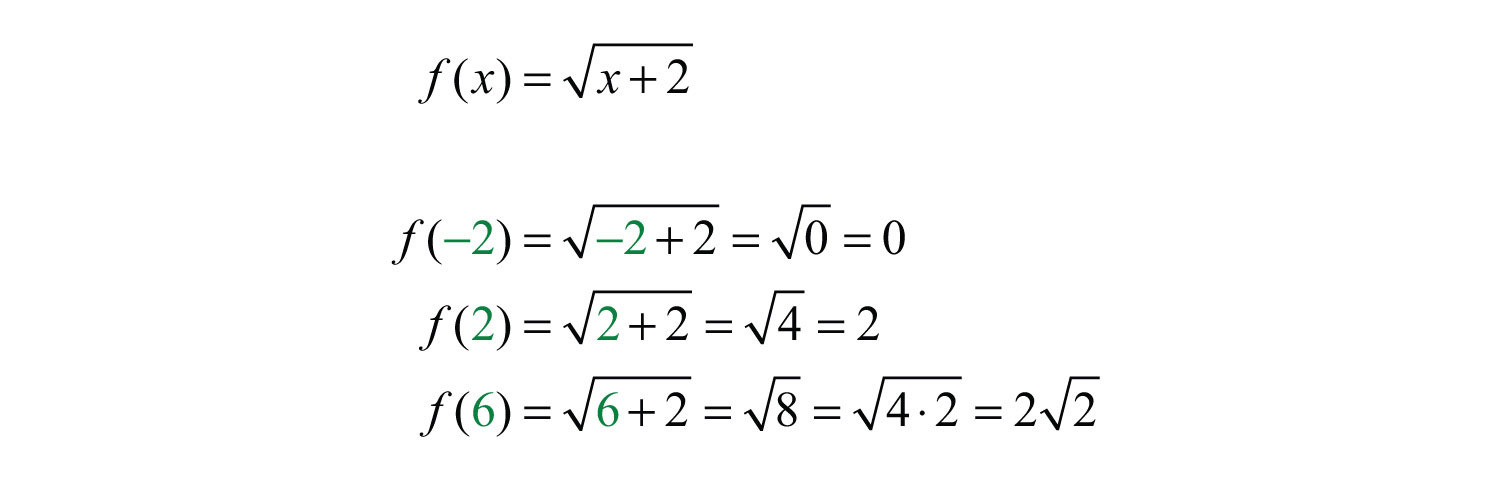
Answer: , , and
Next, consider the cube root functionThe function .:
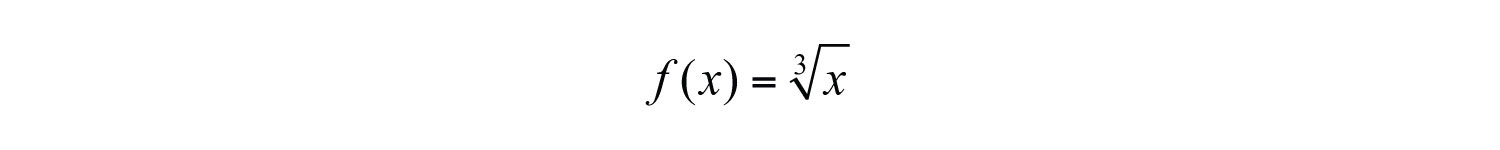
Since the cube root could be either negative or positive, we conclude that the domain consists of all real numbers. For completeness, choose some positive and negative values for x, as well as 0, and then calculate the corresponding y-values.
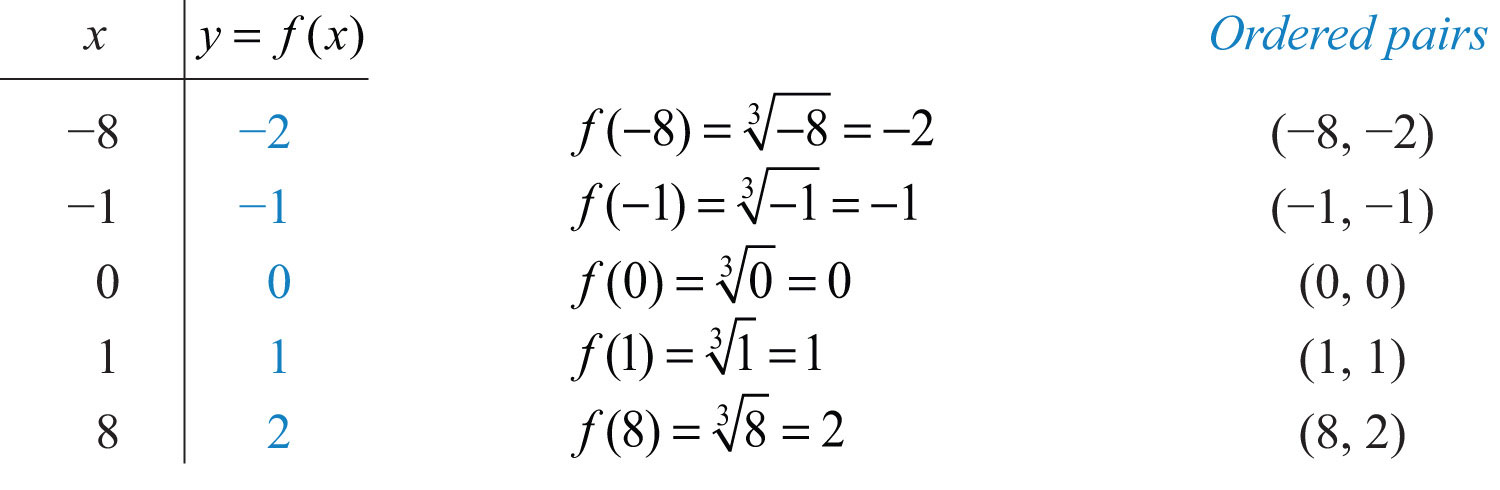
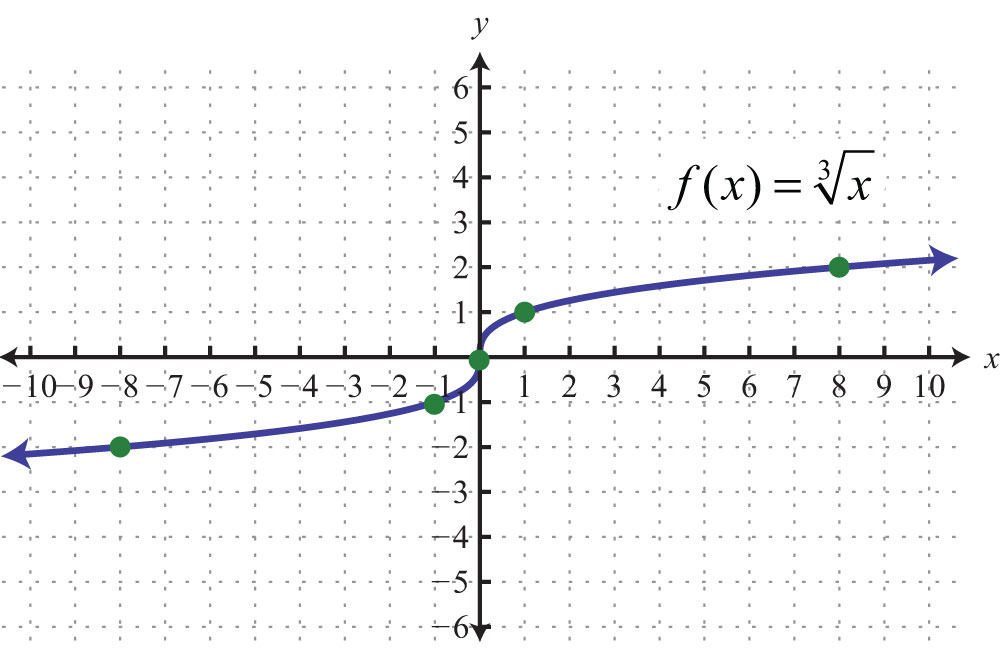
Plot the points and sketch the graph of the cube root function.
Example 12: Given the function , find , , and .
Solution: Replace x with each of the given values.
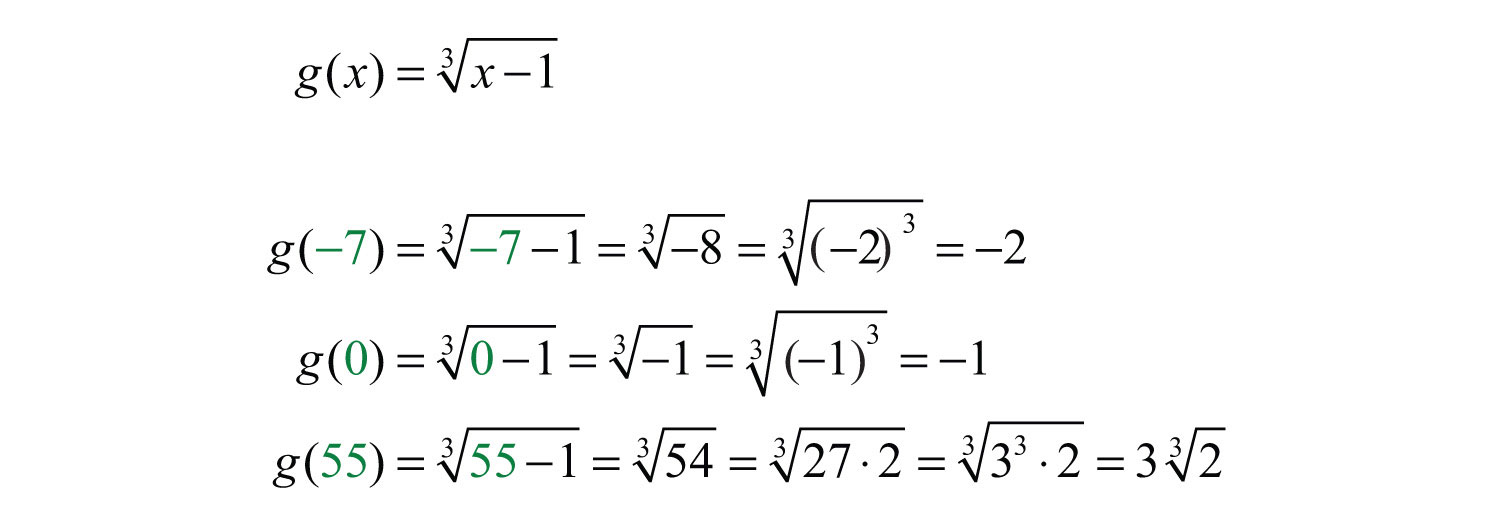
Answer: , , and
Key Takeaways
- In beginning algebra, we typically assume that all variable expressions within the radical are positive. This allows us to focus on simplifying radicals without the technical issues associated with the principal nth root.
- To simplify radical expressions, look for factors of the radicand with powers that match the index. If found, they can be simplified by applying the product and quotient rules for radicals, as well as the property , where a is positive.
Topic Exercises
Part A: Simplifying Radical Expressions
Simplify. (Assume all variables represent positive numbers.)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
Rewrite the following as a radical expression with coefficient 1.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
Assume that the variable could represent any real number and then simplify.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
Part B: Formulas Involving Radicals
The y-intercepts for any graph will have the form (0, y), where y is a real number. Therefore, to find y-intercepts, set x = 0 and solve for y. Find the y-intercepts for the following.
83.
84.
85.
86.
Use the distance formula to calculate the distance between the given two points.
87. (5, −7) and (3, −8)
88. (−9, 7) and (−8, 4)
89. (−3, −4) and (3, −6)
90. (−5, −2) and (1, −6)
91. (−1, 1) and (−4, 10)
92. (8, −3) and (2, −12)
Factor the radicand and then simplify. (Assume that all expressions are positive.)
93.
94.
95.
96.
97. The speed of a vehicle before the brakes were applied can be estimated by the length of the skid marks left on the road. On dry pavement, the speed, v, in miles per hour can be estimated by the formula , where d represents the length of the skid marks in feet. Estimate the speed of a vehicle before applying the brakes on dry pavement if the skid marks left behind measure 36 feet.
98. The radius, r, of a sphere can be calculated using the formula , where V represents the sphere’s volume. What is the radius of a sphere if the volume is cubic centimeters?
The period, T, of a pendulum in seconds is given by the formula
where L represents the length in feet. Calculate the period, given the following lengths. Give the exact value and the approximate value rounded off to the nearest tenth of a second.
99. 8 feet
100. 32 feet
101. 1/2 foot
102. 1/8 foot
The time, t, in seconds that an object is in free fall is given by the formula
where s represents the distance it has fallen in feet. Calculate the time it takes an object to fall, given the following distances. Give the exact value and the approximate value rounded off to the nearest tenth of a second.
103. 48 feet
104. 80 feet
105. 192 feet
106. 288 feet
Part C: Radical Functions
Given the function, calculate the following.
107. , find , , and
108. , find , , and
109. , find , , and
110. , find , , and
111. , find , , and
112. , find , , and
113. , find , , and
114. , find , , and
For each function, fill in the table.
115.
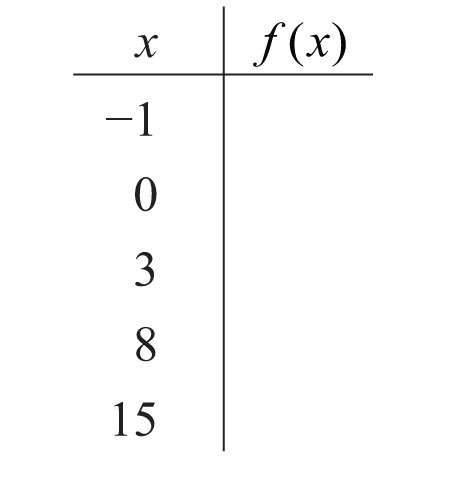
116.
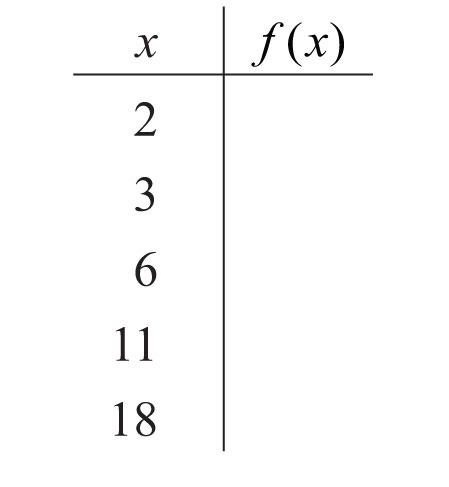
117.
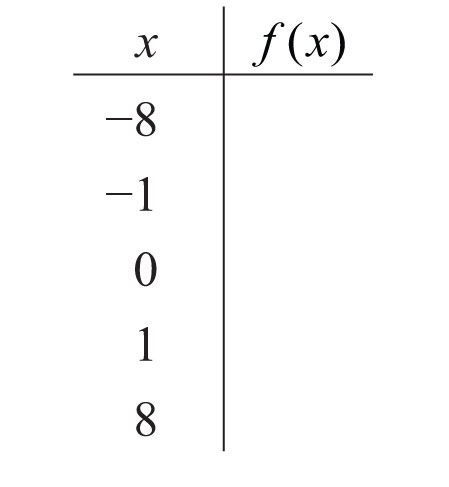
118.
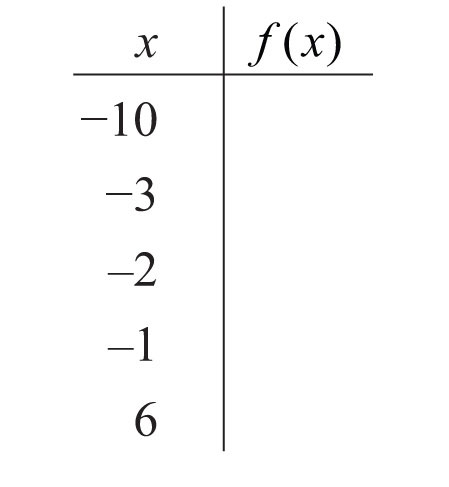
Part D: Discussion Board
119. Give a value for x such that . Explain why it is important to assume that the variables represent positive numbers.
120. Research and discuss the accomplishments of Christoph Rudolff. What is he credited for?
121. Research and discuss the methods used for calculating square roots before the common use of electronic calculators.
122. What is a surd, and where does the word come from?
Answers
1:
3:
5:
7:
9:
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81:
83: (0, 1)
85: (0, 1)
87:
89:
91:
93:
95:
97: 30 miles per hour
99: seconds
101: seconds
103: seconds
105: seconds
107: , , and
109: , , and
111: , , and
113: , , and
115:
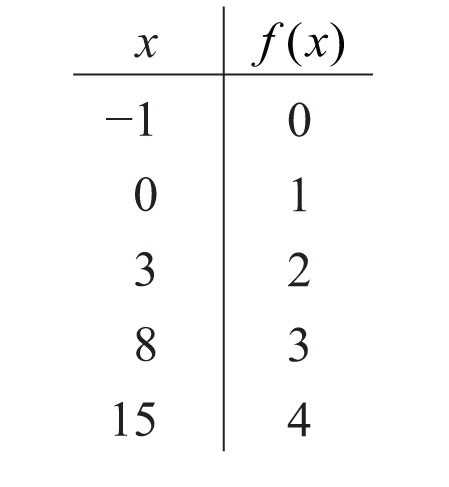
117: