Complex Rational Expressions

7.4 Complex Rational Expressions

Learning Objectives

Simplify complex rational expressions by multiplying the numerator by the reciprocal of the divisor.
Simplify complex rational expressions by multiplying numerator and denominator by the least common denominator (LCD).

Definitions

A complex fractionA fraction where the numerator or denominator consists of one or more fractions. is a fraction where the numerator or denominator consists of one or more fractions. For example,

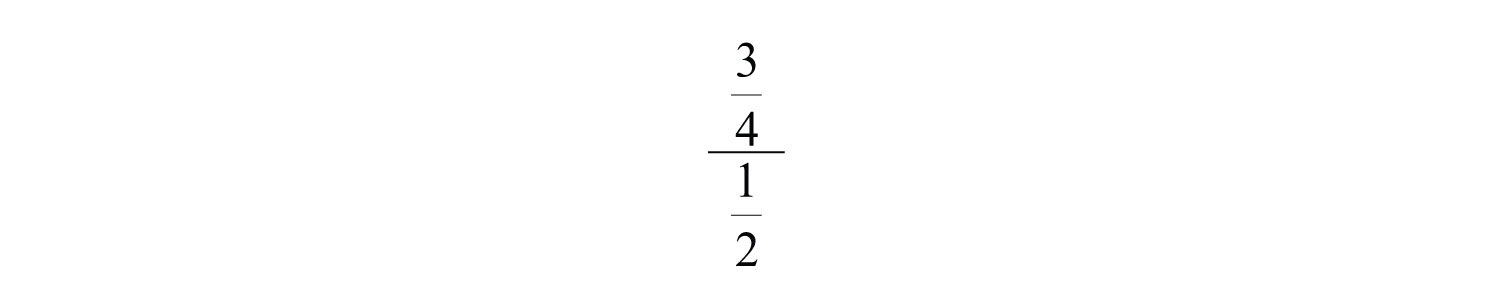
Simplifying such a fraction requires us to find an equivalent fraction with integer numerator and denominator. One way to do this is to divide. Recall that dividing fractions involves multiplying by the reciprocal of the divisor.

An alternative method for simplifying this complex fraction involves multiplying both the numerator and denominator by the LCD of all the given fractions. In this case, the LCD = 4.

A complex rational expressionA rational expression where the numerator or denominator consists of one or more rational expressions. is defined as a rational expression that contains one or more rational expressions in the numerator or denominator or both. For example,

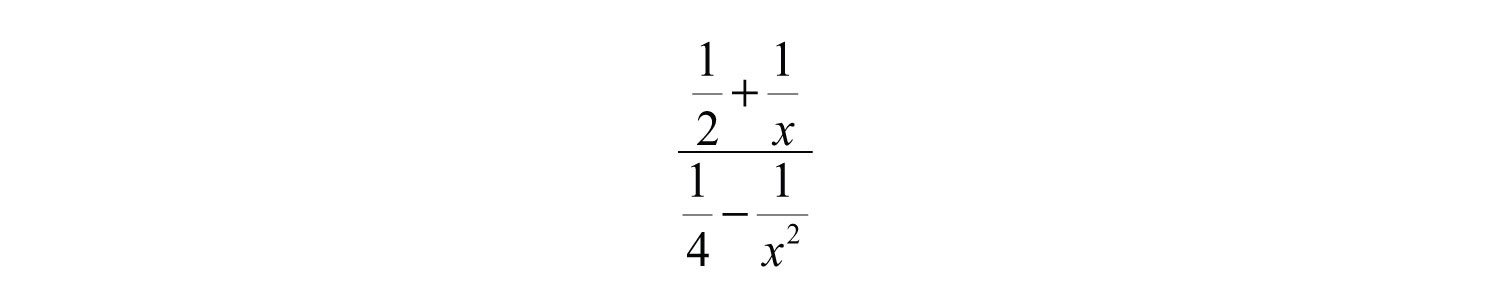
We simplify a complex rational expression by finding an equivalent fraction where the numerator and denominator are polynomials. As illustrated above, there are two methods for simplifying complex rational expressions, and we will outline the steps for both methods. For the sake of clarity, assume that variable expressions used as denominators are nonzero.

Method 1: Simplify Using Division

We begin our discussion on simplifying complex rational expressions using division. Before we can multiply by the reciprocal of the divisor, we must simplify the numerator and denominator separately. The goal is to first obtain single algebraic fractions in the numerator and the denominator. The steps for simplifying a complex algebraic fraction are illustrated in the following example.

Example 1: Simplify: $\frac{\frac{1}{2} + \frac{1}{x}}{\frac{1}{4} - \frac{1}{x^{2}}}$ .

Solution:

Step 1: Simplify the numerator and denominator. The goal is to obtain a single algebraic fraction divided by another single algebraic fraction. In this example, find equivalent terms with a common denominator in both the numerator and denominator before adding and subtracting.

At this point we have a single algebraic fraction divided by a single algebraic fraction.

Step 2: Multiply the numerator by the reciprocal of the divisor.

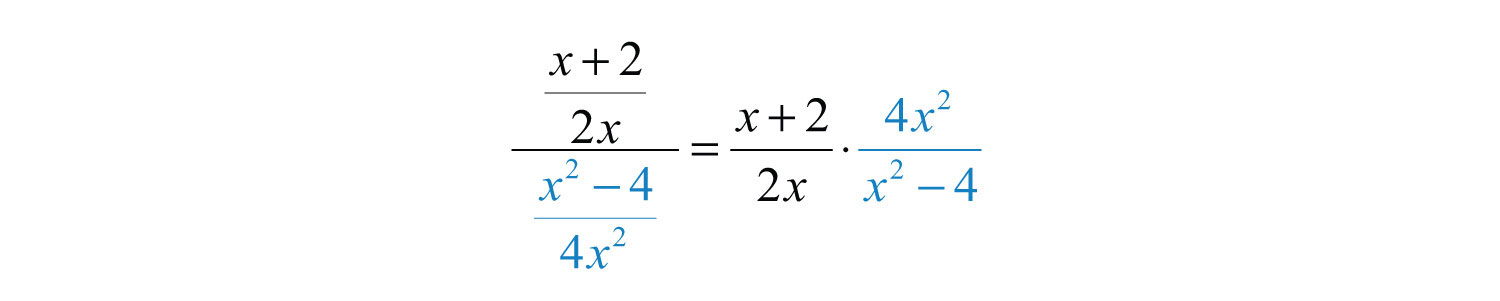
Step 3: Factor all numerators and denominators completely.

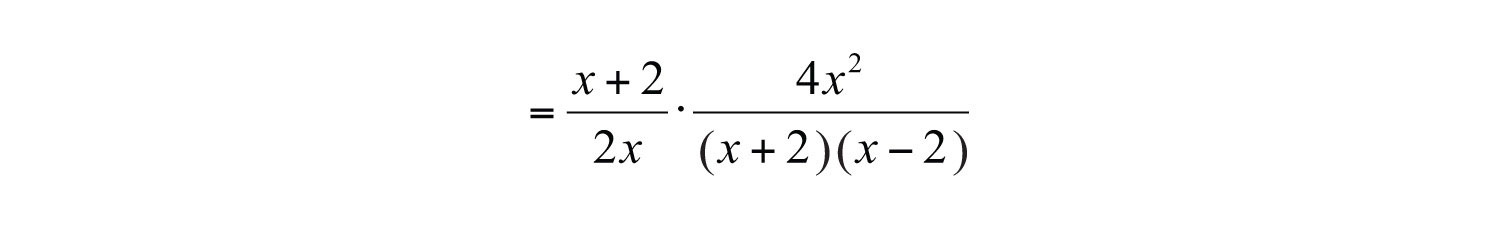
Step 4: Cancel all common factors.

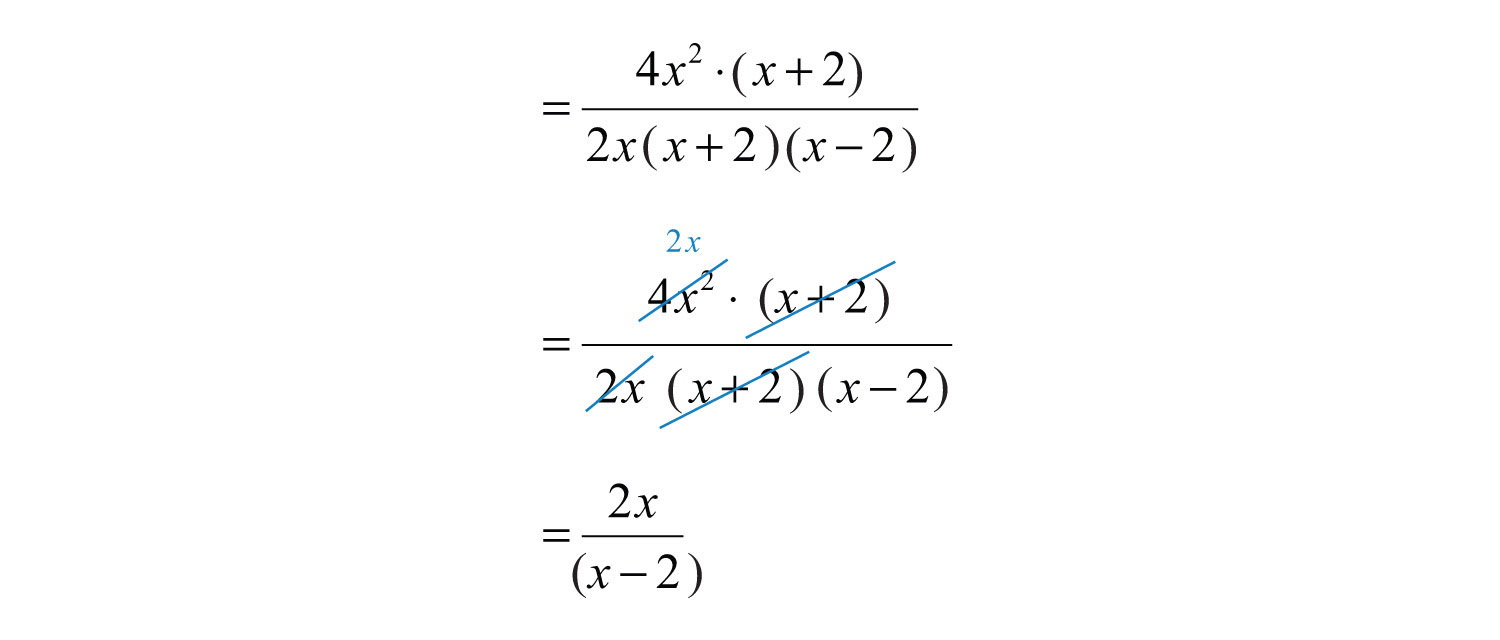
Answer: $\frac{2 x}{x - 2}$

Example 2: Simplify: $\frac{\frac{1}{x} - \frac{1}{x - 2}}{\frac{4}{x^{2} - 2 x}}$ .

Solution:

Answer: $- \frac{1}{2}$

Example 3: Simplify $\frac{1 - \frac{4}{x} - \frac{21}{x^{2}}}{1 - \frac{2}{x} - \frac{15}{x^{2}}}$ .

Solution: The LCD of the rational expressions in both the numerator and denominator is $x^{2}$ . Multiply by the appropriate factors to obtain equivalent terms with this as the denominator and then subtract.

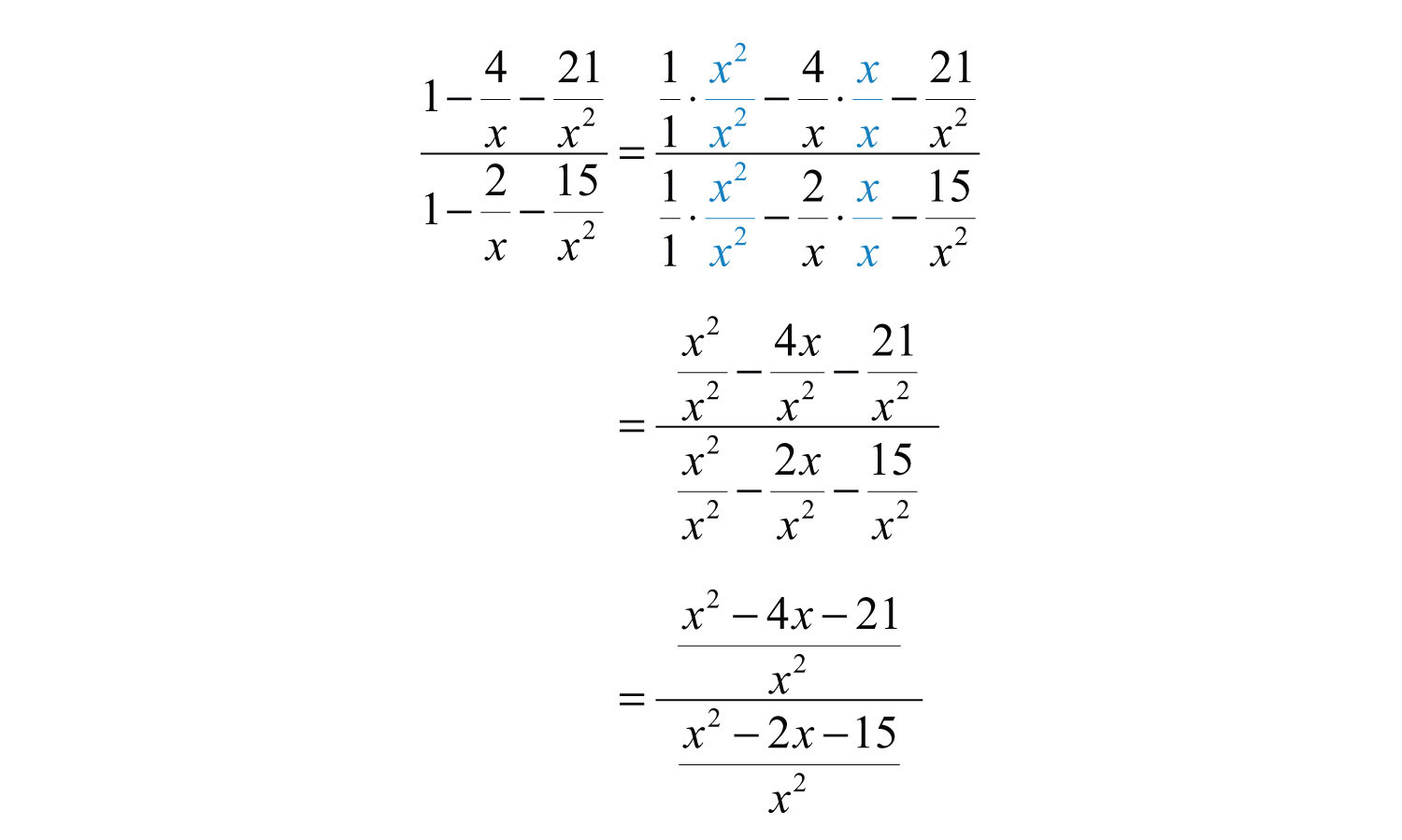
We now have a single rational expression divided by another single rational expression. Next, multiply the numerator by the reciprocal of the divisor and then factor and cancel.

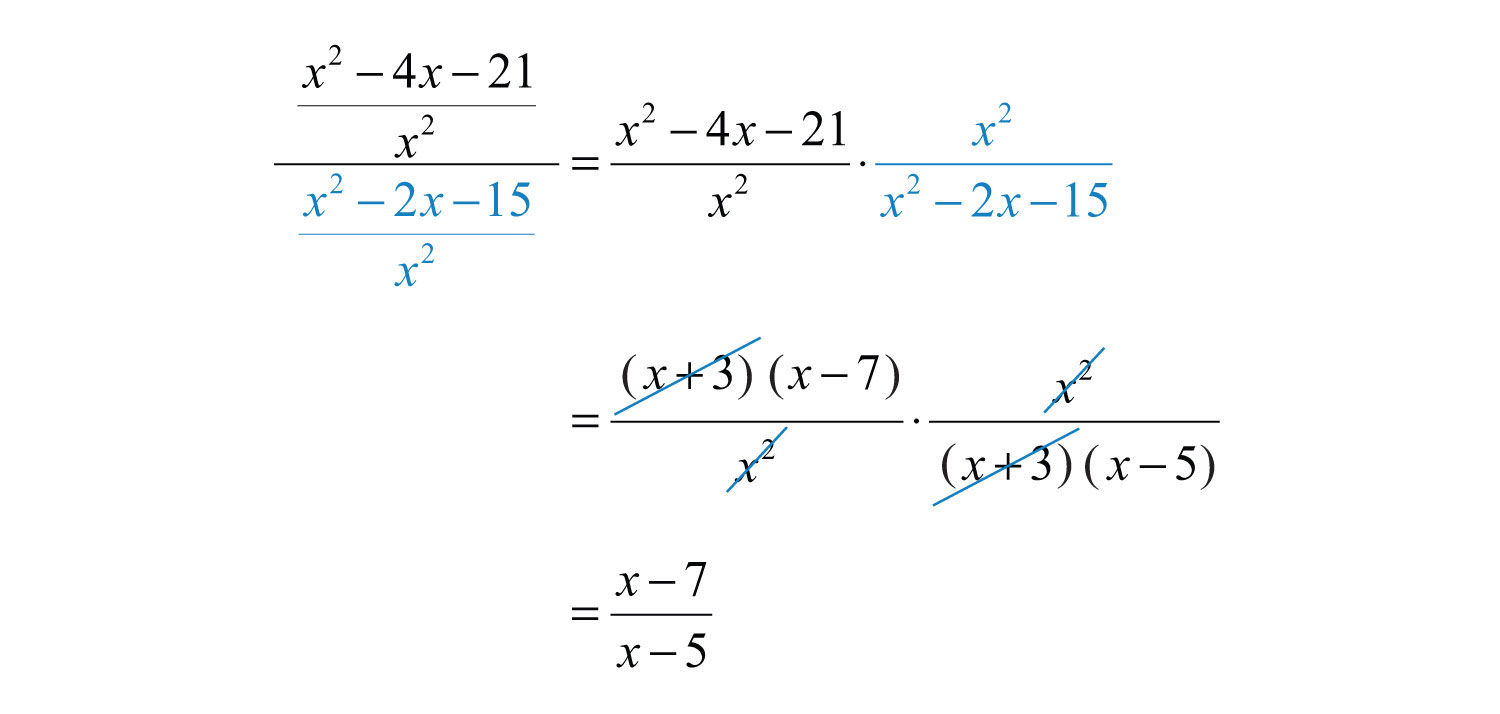
Answer: $\frac{x - 7}{x - 5}$

Example 4: Simplify: $\frac{1 - \frac{1}{x^{2}}}{\frac{1}{x} - 1}$ .

Solution:

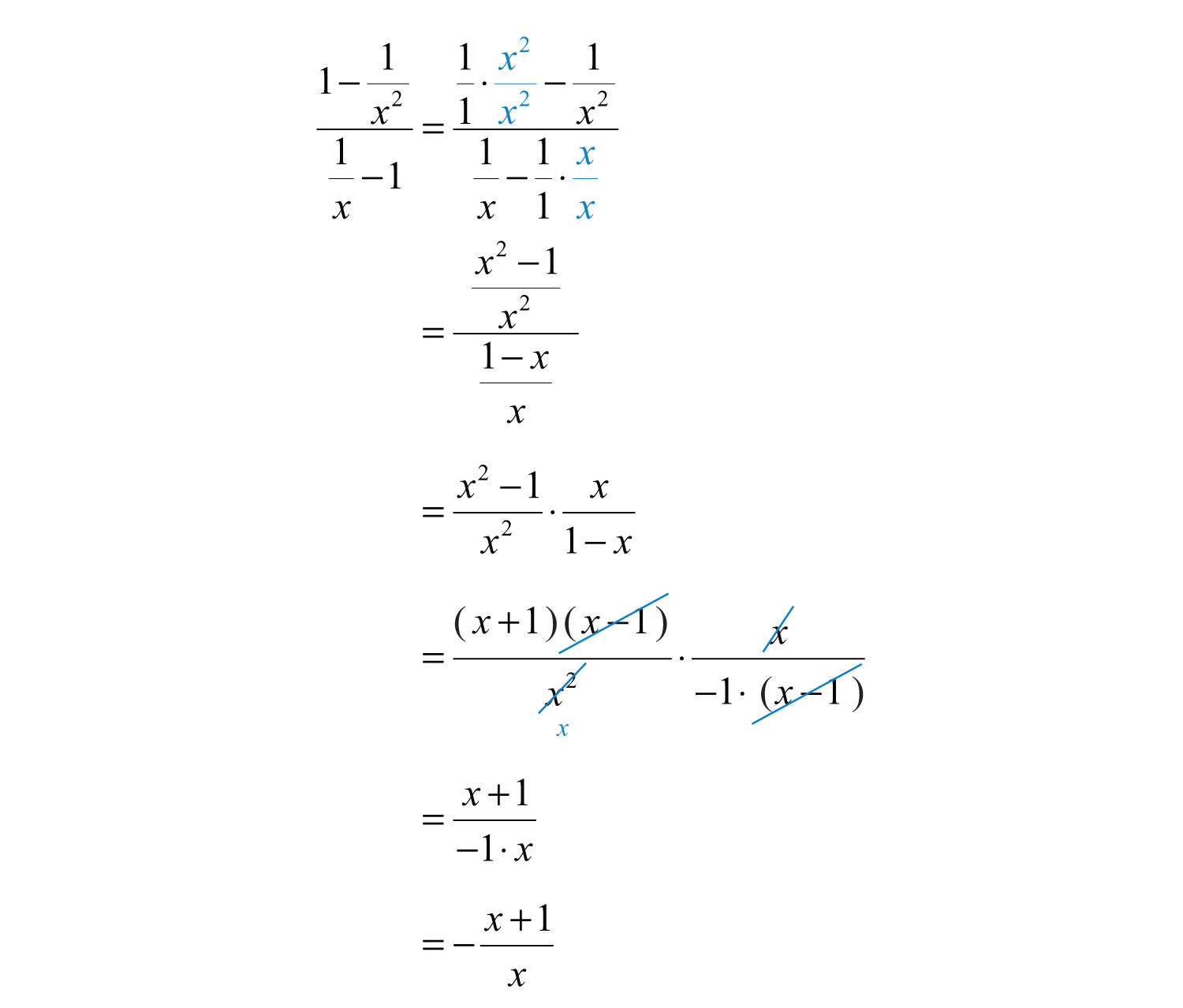
Answer: $- \frac{x + 1}{x}$

Try this! Simplify: $\frac{\frac{1}{81} - \frac{1}{x^{2}}}{\frac{1}{9} + \frac{1}{x}}$ .

Answer: $\frac{x - 9}{9 x}$

Video Solution

(click to see video)

Method 2: Simplify Using the LCD

An alternative method for simplifying complex rational expressions involves clearing the fractions by multiplying the expression by a special form of 1. In this method, multiply the numerator and denominator by the least common denominator (LCD) of all given fractions.

Example 5: Simplify: $\frac{\frac{1}{2} + \frac{1}{x}}{\frac{1}{4} - \frac{1}{x^{2}}}$ .

Solution:

Step 1: Determine the LCD of all the fractions in the numerator and denominator. In this case, the denominators of the given fractions are 2, $x$ , 4, and $x^{2}$ . Therefore, the $L C D is 4 x^{2}$ .

Step 2: Multiply the numerator and denominator by the LCD. This step should clear the fractions in both the numerator and denominator.

This leaves us with a single algebraic fraction with a polynomial in the numerator and in the denominator.

Step 3: Factor the numerator and denominator completely.

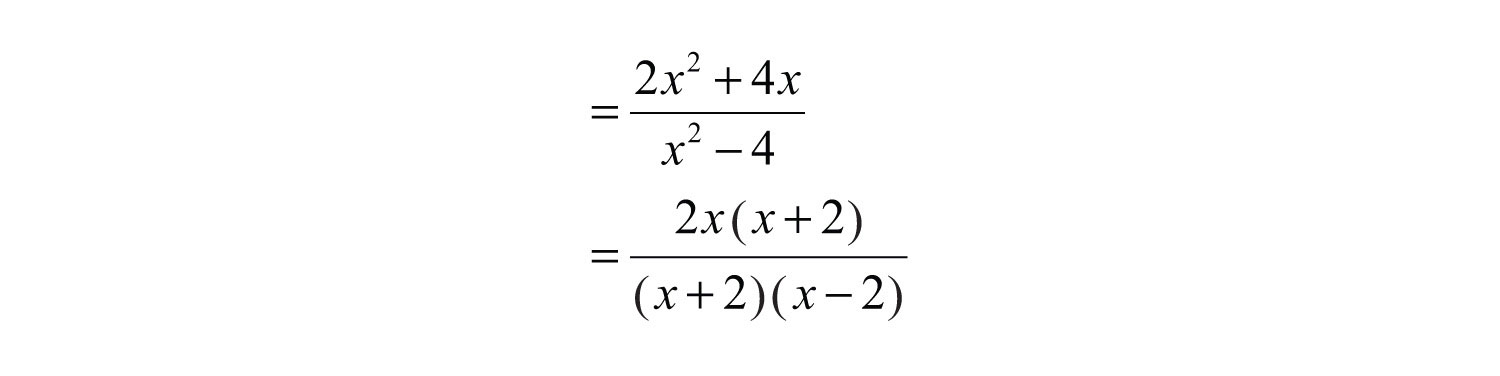
Step 4: Cancel all common factors.

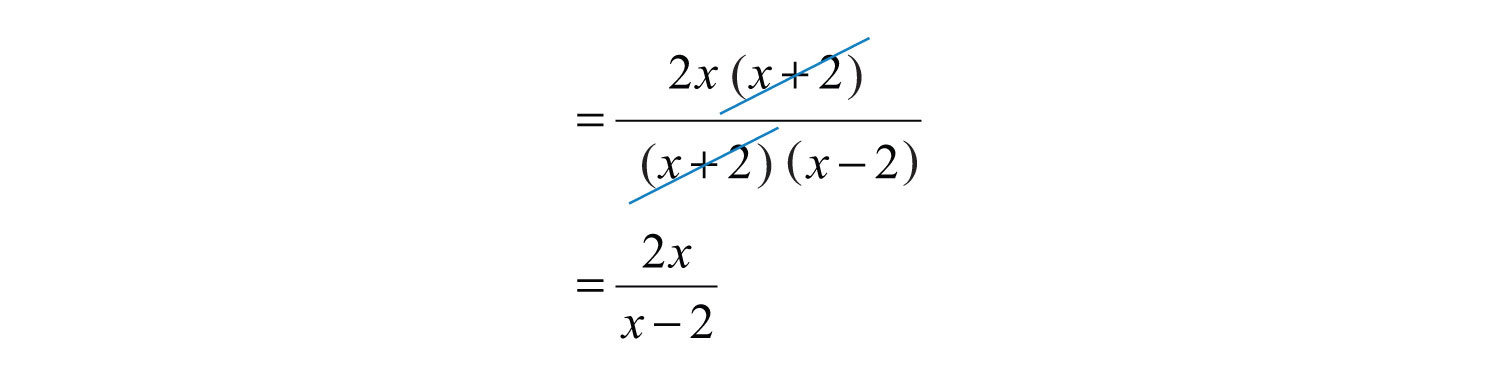
Answer: $\frac{2 x}{x - 2}$

Note

This was the same problem that we began this section with, and the results here are the same. It is worth taking the time to compare the steps involved using both methods on the same problem.

Example 6: Simplify: $\frac{1 - \frac{2}{x} - \frac{15}{x^{2}}}{3 - \frac{14}{x} - \frac{5}{x^{2}}}$ .

Solution: Considering all of the denominators, we find that the $LCD is x^{2}$ . Therefore, multiply the numerator and denominator by $x^{2}$ :

At this point, we have a rational expression that can be simplified by factoring and then canceling the common factors.

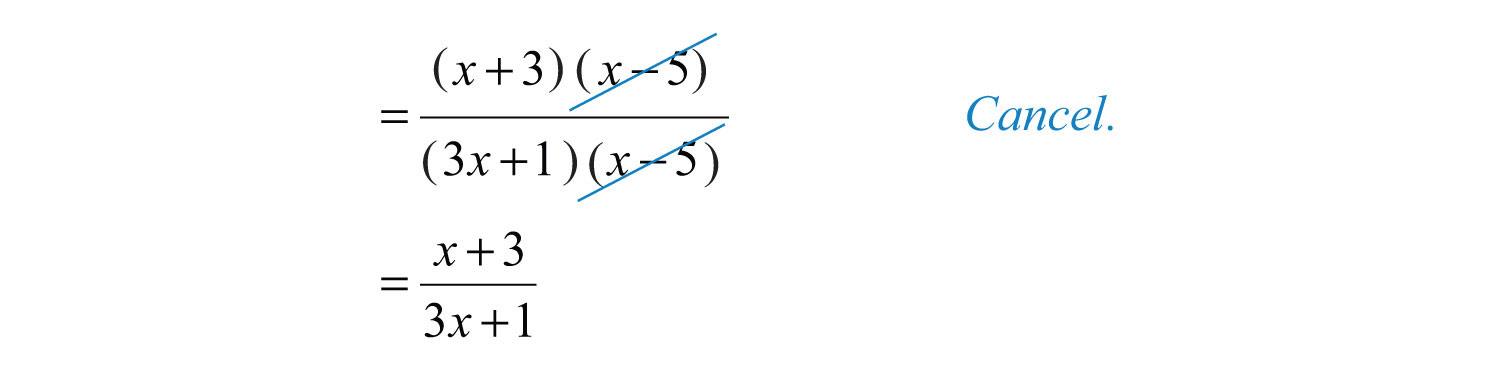
Answer: $\frac{x + 3}{3 x + 1}$

It is important to point out that multiplying the numerator and denominator by the same nonzero factor is equivalent to multiplying by 1 and does not change the problem. Because $\frac{x^{2}}{x^{2}} = 1$ , we can multiply the numerator and denominator by $x^{2}$ in the previous example and obtain an equivalent expression.

Example 7: Simplify: $\frac{\frac{1}{x + 1} + \frac{3}{x - 3}}{\frac{2}{x - 3} - \frac{1}{x + 1}}$ .

Solution: The LCM of all the denominators is $(x + 1) (x - 3)$ . Begin by multiplying the numerator and denominator by these factors.

Answer: $\frac{4 x}{x + 5}$

Try this! Simplify: $\frac{\frac{1}{y} - \frac{1}{4}}{\frac{1}{16} - \frac{1}{y^{2}}}$ .

Answer: $- \frac{4 y}{y + 4}$

Video Solution

(click to see video)

Key Takeaways

Complex rational expressions can be simplified into equivalent expressions with a polynomial numerator and polynomial denominator.
One method of simplifying a complex rational expression requires us to first write the numerator and denominator as a single algebraic fraction. Then multiply the numerator by the reciprocal of the divisor and simplify the result.
Another method for simplifying a complex rational expression requires that we multiply it by a special form of 1. Multiply the numerator and denominator by the LCM of all the denominators as a means to clear the fractions. After doing this, simplify the remaining rational expression.
An algebraic fraction is reduced to lowest terms if the numerator and denominator are polynomials that share no common factors other than 1.

Topic Exercises

Part A: Complex Rational Expressions

Simplify. (Assume all denominators are nonzero.)

1. $\frac{\frac{1}{2}}{\frac{5}{4}}$

2. $\frac{\frac{7}{8}}{\frac{5}{4}}$

3. $\frac{\frac{10}{3}}{\frac{20}{9}}$

4. $\frac{- \frac{4}{21}}{\frac{8}{7}}$

5. $\frac{\frac{2}{3}}{\frac{5}{6}}$

6. $\frac{\frac{7}{4}}{\frac{14}{3}}$

7. $\frac{1 - \frac{3}{2}}{\frac{5}{4} - \frac{1}{3}}$

8. $\frac{\frac{1}{2} - 5}{\frac{1}{2} + \frac{1}{3}}$

9. $\frac{1 + \frac{3}{2}}{1 - \frac{1}{4}}$

10. $\frac{2 - \frac{1}{2}}{1 + \frac{3}{4}}$

11. $\frac{\frac{5 x^{2}}{x + 1}}{\frac{25 x}{x + 1}}$

12. $\frac{\frac{7 + x}{7 x}}{\frac{x + 7}{14 x^{2}}}$

13. $\frac{\frac{3 y}{x}}{\frac{y^{2}}{x - 1}}$

14. $\frac{\frac{5 a^{2}}{b - 1}}{\frac{15 a^{3}}{{(b - 1)}^{2}}}$

15. $\frac{1 + \frac{1}{x}}{2 - \frac{1}{x}}$

16. $\frac{\frac{2}{x} + 1}{3 - \frac{1}{x}}$

17. $\frac{\frac{2}{3 y} - 4}{6 - \frac{1}{y}}$

18. $\frac{\frac{5}{y} - \frac{1}{2}}{\frac{10 - y}{y^{2}}}$

19. $\frac{\frac{1}{5} - \frac{1}{x}}{\frac{1}{25} - \frac{1}{x^{2}}}$

20. $\frac{\frac{1}{x} + \frac{1}{5}}{\frac{1}{25} - \frac{1}{x^{2}}}$

21. $\frac{\frac{1}{x} - \frac{1}{3}}{\frac{1}{9} - \frac{1}{x^{2}}}$

22. $\frac{\frac{1}{4} + \frac{1}{x}}{\frac{1}{x^{2}} - \frac{1}{16}}$

23. $\frac{16 - \frac{1}{x^{2}}}{\frac{1}{x} - 4}$

24. $\frac{2 - \frac{1}{y}}{1 - \frac{1}{4 y^{2}}}$

25. $\frac{\frac{1}{x} + \frac{1}{y}}{\frac{1}{y^{2}} - \frac{1}{x^{2}}}$

26. $\frac{\frac{1}{2 x} - \frac{4}{3}}{\frac{1}{4 x^{2}} - \frac{16}{9}}$

27. $\frac{\frac{2}{25} - \frac{1}{2 x^{2}}}{\frac{1}{5} - \frac{1}{2 x}}$

28. $\frac{\frac{4}{25} - \frac{1}{4 x^{2}}}{\frac{1}{5} + \frac{1}{4 x}}$

29. $\frac{\frac{1}{y} - \frac{1}{x}}{4 - \frac{2}{x y}}$

30. $\frac{\frac{1}{a b} + 2}{\frac{1}{a} + \frac{1}{b}}$

31. $\frac{\frac{1}{y} + \frac{1}{x}}{x y}$

32. $\frac{3 x}{\frac{1}{3} - \frac{1}{x}}$

33. $\frac{1 - \frac{4}{x} - \frac{21}{x^{2}}}{1 - \frac{2}{x} - \frac{15}{x^{2}}}$

34. $\frac{1 - \frac{3}{x} - \frac{4}{x^{2}}}{1 - \frac{16}{x^{2}}}$

35. $\frac{3 - \frac{1}{2 x} - \frac{1}{2 x^{2}}}{2 - \frac{2}{x} + \frac{1}{2 x^{2}}}$

36. $\frac{\frac{1}{2} - \frac{5}{x} + \frac{12}{x^{2}}}{\frac{1}{2} - \frac{6}{x} + \frac{18}{x^{2}}}$

37. $\frac{\frac{1}{x} - \frac{4}{3 x^{2}}}{3 - \frac{8}{x} + \frac{16}{3 x^{2}}}$

38. $\frac{1 + \frac{3}{10 x} - \frac{1}{10 x^{2}}}{\frac{3}{5} - \frac{1}{10 x} - \frac{1}{5 x^{2}}}$

39. $\frac{x - 1}{1 + \frac{4}{x} - \frac{5}{x^{2}}}$

40. $\frac{2 - \frac{5}{2 x} - \frac{3}{x^{2}}}{4 x + 3}$

41. $\frac{\frac{1}{x - 3} + \frac{2}{x}}{\frac{1}{x} - \frac{3}{x - 3}}$

42. $\frac{\frac{1}{4 x - 5} + \frac{1}{x^{2}}}{\frac{1}{x^{2}} + \frac{1}{3 x - 10}}$

43. $\frac{\frac{1}{x + 5} + \frac{4}{x - 2}}{\frac{2}{x - 2} - \frac{1}{x + 5}}$

44. $\frac{\frac{3}{x - 1} - \frac{2}{x + 3}}{\frac{2}{x + 3} + \frac{1}{x - 3}}$

45. $\frac{\frac{x}{x + 1} - \frac{2}{x + 3}}{\frac{x}{3 x + 4} + \frac{1}{x + 1}}$

46. $\frac{\frac{x}{x - 9} + \frac{2}{x + 1}}{\frac{x}{7 x - 9} - \frac{1}{x + 1}}$

47. $\frac{\frac{x}{3 x + 2} - \frac{1}{x + 2}}{\frac{x}{x + 2} - \frac{2}{x + 2}}$

48. $\frac{\frac{x}{x - 4} + \frac{1}{x + 2}}{\frac{x}{3 x + 4} + \frac{1}{x + 2}}$

49. $\frac{\frac{a^{3} - 8 b^{3}}{27}}{a - 2 b}$

50. $\frac{\frac{27 a^{3} + b^{3}}{a b}}{3 a + b}$

51. $\frac{\frac{1}{b^{3}} + \frac{1}{a^{3}}}{\frac{1}{b} + \frac{1}{a}}$

52. $\frac{\frac{1}{b^{3}} - \frac{1}{a^{3}}}{\frac{1}{a} - \frac{1}{b}}$

53. $\frac{\frac{x^{2} + y^{2}}{x y} + 2}{\frac{x^{2} - y^{2}}{2 x y}}$

54. $\frac{\frac{x}{y} + 4 + \frac{4 y}{x}}{\frac{x}{y} + 3 + \frac{2 y}{x}}$

55. $1 + \frac{1}{1 + \frac{1}{2}}$

56. $2 - \frac{1}{1 + \frac{1}{3}}$

57. $\frac{1}{1 + \frac{1}{1 + x}}$

58. $\frac{\frac{x + 1}{x}}{1 - \frac{1}{x + 1}}$

59. $\frac{1 - \frac{1}{x}}{x - \frac{1}{x}}$

60. $\frac{\frac{1}{x} - x}{\frac{x - 1}{x^{2}}}$

Part B: Discussion Board Topics

61. Choose a problem from this exercise set and clearly work it out on paper, explaining each step in words. Scan your page and post it on the discussion board.

62. Explain why we need to simplify the numerator and denominator to a single algebraic fraction before multiplying by the reciprocal of the divisor.

63. Two methods for simplifying complex rational expressions have been presented in this section. Which of the two methods do you feel is more efficient, and why?

Answers

1: $\frac{2}{5}$

3: $\frac{3}{2}$

5: 4/5

7: −6/11

9: $\frac{10}{3}$

11: $\frac{x}{5}$

13: $\frac{3 (x - 1)}{x y}$

15: $\frac{x + 1}{2 x - 1}$

17: $- \frac{2}{3}$

19: $\frac{5 x}{x + 5}$

21: $- \frac{3 x}{x + 3}$

23: $- \frac{4 x + 1}{x}$

25: $\frac{x y}{x - y}$

27: $\frac{2 x + 5}{5 x}$

29: $\frac{x - y}{4 x y - 2}$

31: $\frac{x + y}{x^{2} y^{2}}$

33: $\frac{x - 7}{x - 5}$

35: $\frac{3 x + 1}{2 x - 1}$

37: $\frac{1}{3 x - 4}$

39: $\frac{x^{2}}{x + 5}$

41: $- \frac{3 (x - 2)}{2 x + 3}$

43: $\frac{5 x + 18}{x + 12}$

45: $\frac{(x - 1) (3 x + 4)}{(x + 2) (x + 3)}$

47: $\frac{x + 1}{3 x + 2}$

49: $\frac{a^{2} + 2 a b + 4 b^{2}}{27}$

51: $\frac{a^{2} - a b + b^{2}}{a^{2} b^{2}}$

53: $\frac{2 (x + y)}{x - y}$

55: $\frac{5}{3}$

57: $\frac{x + 1}{x + 2}$

59: $\frac{1}{x + 1}$