Multiplying and Dividing Rational Expressions

7.2 Multiplying and Dividing Rational Expressions

Learning Objectives

Multiply rational expressions.
Divide rational expressions.
Multiply and divide rational functions.

Multiplying Rational Expressions

When multiplying fractions, we can multiply the numerators and denominators together and then reduce, as illustrated:

Multiplying rational expressions is performed in a similar manner. For example,

In general, given polynomials P, Q, R, and S, where $Q \neq 0$ and $S \neq 0$ , we have

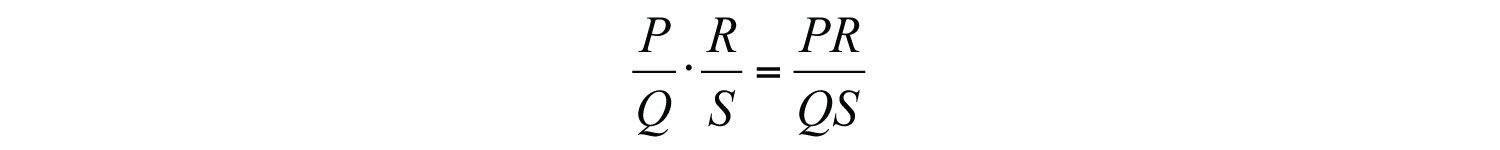
In this section, assume that all variable expressions in the denominator are nonzero unless otherwise stated.

Example 1: Multiply: $\frac{12 x^{2}}{5 y^{3}} \cdot \frac{20 y^{4}}{6 x^{3}}$ .

Solution: Multiply numerators and denominators and then cancel common factors.

Answer: $\frac{8 y}{x}$

Example 2: Multiply: $\frac{x - 3}{x + 5} \cdot \frac{x + 5}{x + 7}$ .

Solution: Leave the product in factored form and cancel the common factors.

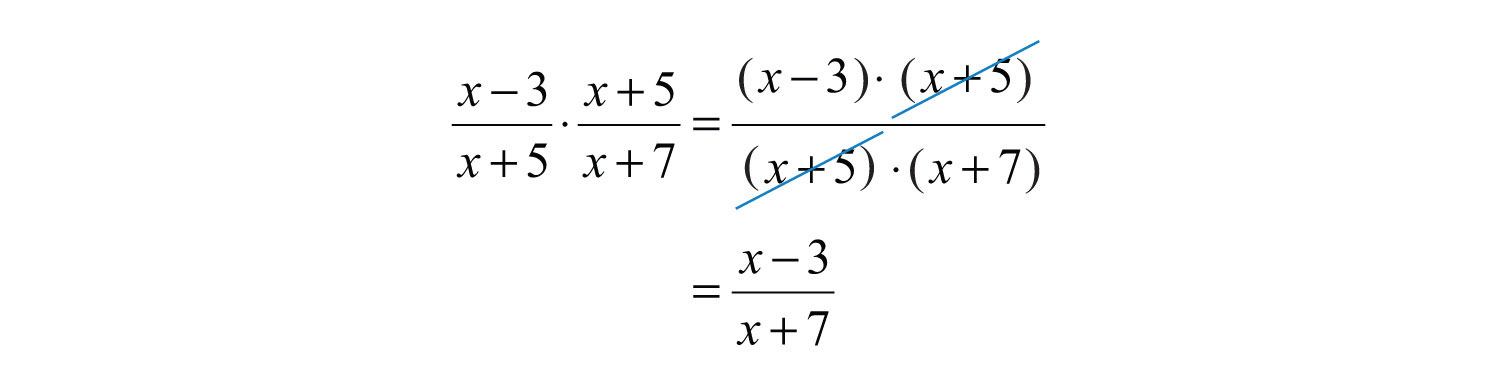
Answer: $\frac{x - 3}{x + 7}$

Example 3: Multiply: $\frac{15 x^{2} y^{3}}{(2 x - 1)} \cdot \frac{x (2 x - 1)}{3 x^{2} y (x + 3)}$ .

Solution: Leave the polynomials in the numerator and denominator factored so that we can cancel the factors. In other words, do not apply the distributive property.

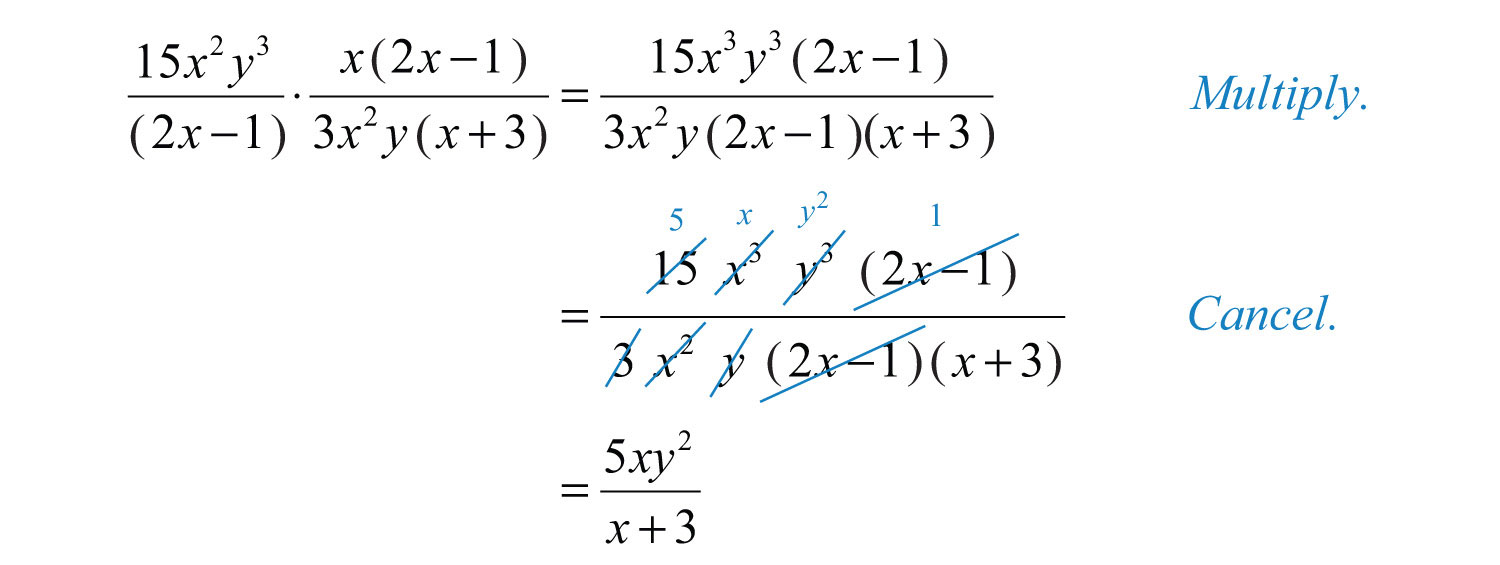
Answer: $\frac{5 x y^{2}}{x + 3}$

Typically, rational expressions will not be given in factored form. In this case, first factor all numerators and denominators completely. Next, multiply and cancel any common factors, if there are any.

Example 4: Multiply: $\frac{x + 5}{x - 5} \cdot \frac{x - 5}{x^{2} - 25}$ .

Solution: Factor the denominator $x^{2} - 25$ as a difference of squares. Then multiply and cancel.

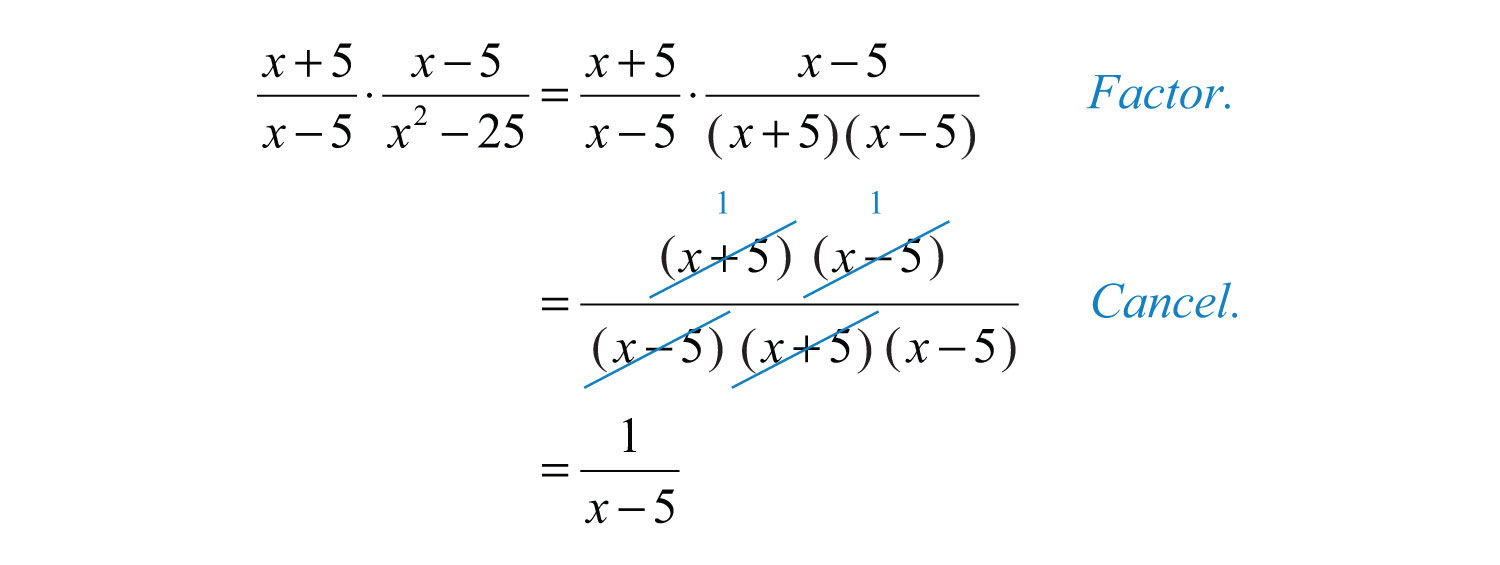
Keep in mind that 1 is always a factor; so when the entire numerator cancels out, make sure to write the factor 1.

Answer: $\frac{1}{x - 5}$

Example 5: Multiply: $\frac{x^{2} + 3 x + 2}{x^{2} - 5 x + 6} \cdot \frac{x^{2} - 7 x + 12}{x^{2} + 8 x + 7}$ .

Solution:

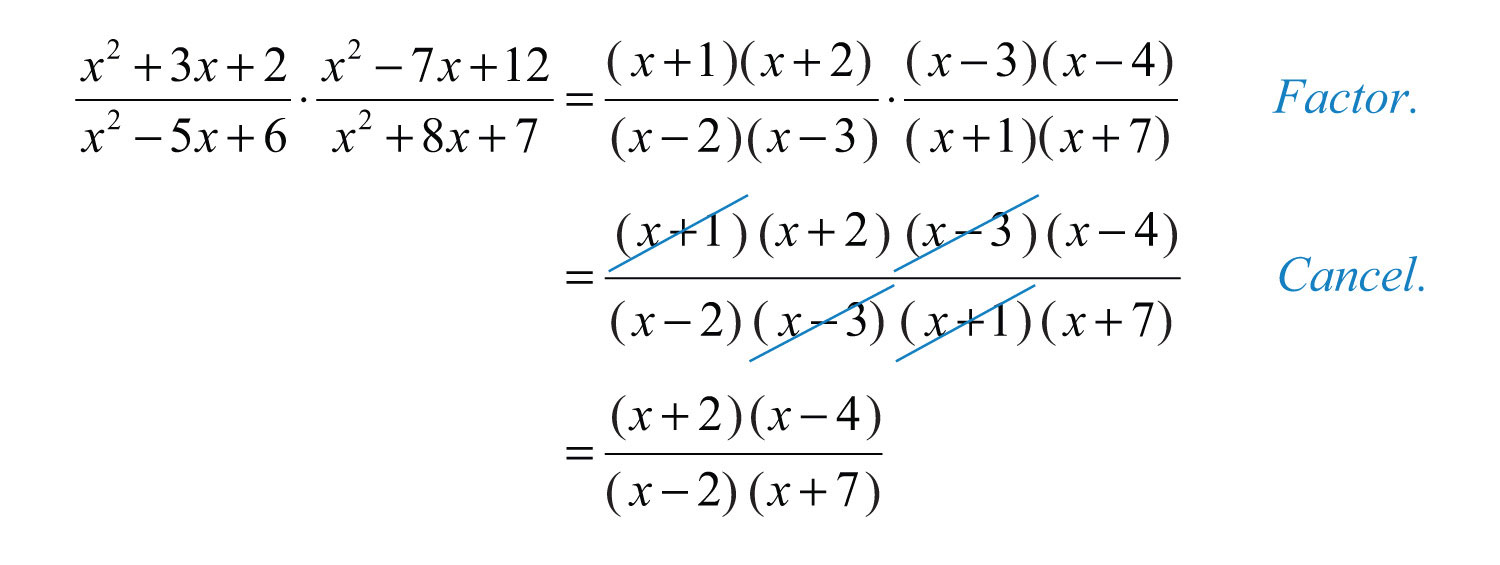
It is a best practice to leave the final answer in factored form.

Answer: $\frac{(x + 2) (x - 4)}{(x - 2) (x + 7)}$

Example 6: Multiply: $\frac{- 2 x^{2} + x + 3}{x^{2} + 2 x - 8} \cdot \frac{3 x - 6}{x^{2} + x}$ .

Solution: The trinomial $- 2 x^{2} + x + 3$ in the numerator has a negative leading coefficient. Recall that it is a best practice to first factor out a −1 and then factor the resulting trinomial.

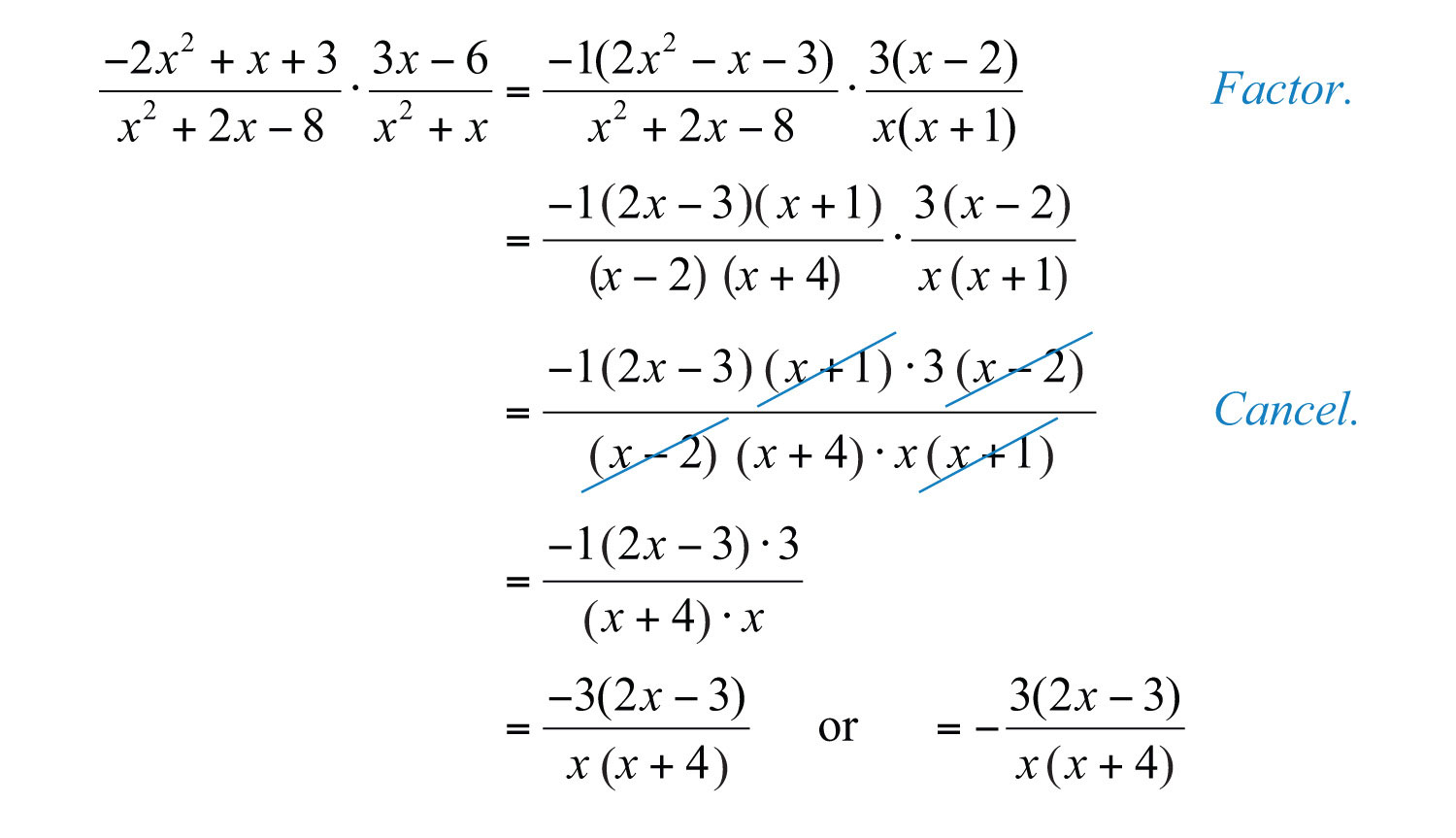
Answer: $- \frac{3 (2 x - 3)}{x (x + 4)}$

Example 7: Multiply: $\frac{7 - x}{x^{2} + 3 x} \cdot \frac{x^{2} + 10 x + 21}{x^{2} - 49}$ .

Solution: We replace $7 - x$ with $- 1 (x - 7)$ so that we can cancel this factor.

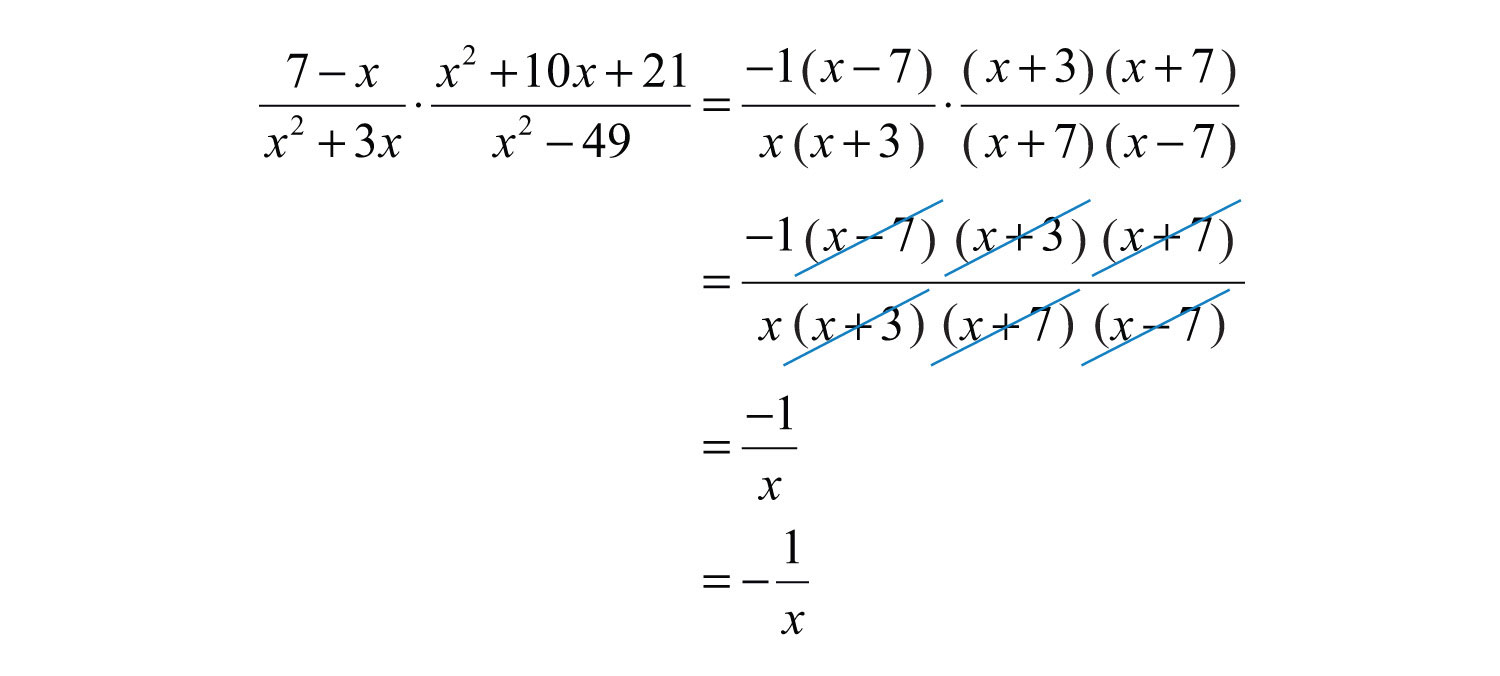
Answer: $- \frac{1}{x}$

Try this! Multiply: $\frac{x^{2} - 64}{8 - x} \cdot \frac{x + x^{2}}{x^{2} + 9 x + 8}$ .

Answer: $- x$

Video Solution

(click to see video)

Dividing Rational Expressions

To divide two fractions, we multiply by the reciprocal of the divisor, as illustrated:

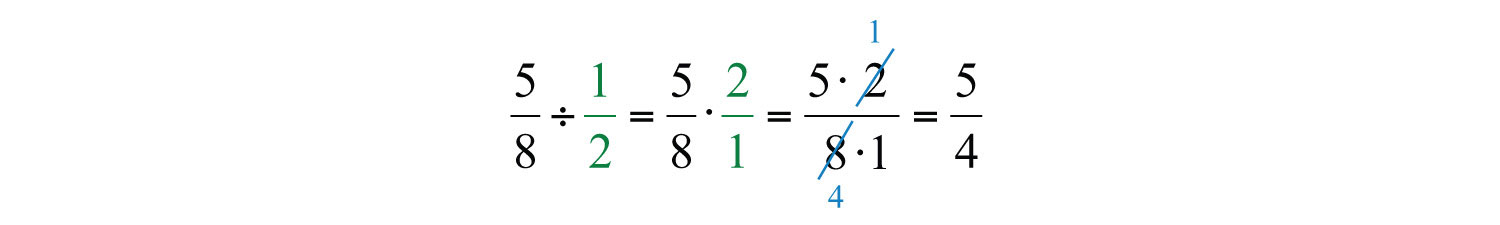
Dividing rational expressions is performed in a similar manner. For example,

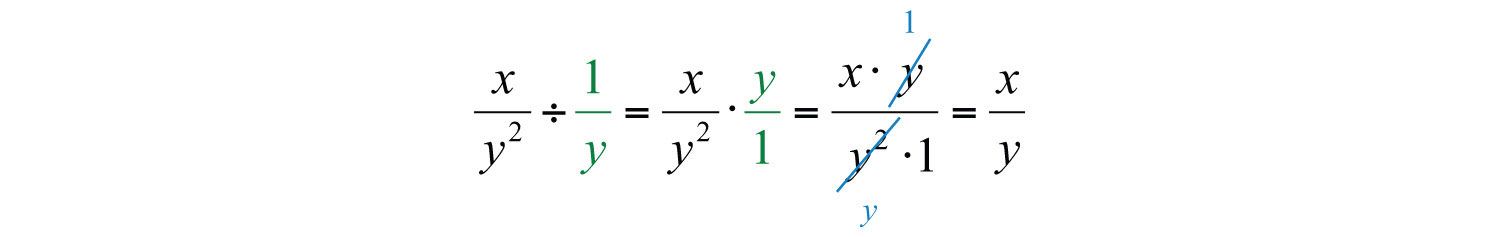
In general, given polynomials P, Q, R, and S, where $Q \neq 0$ , $R \neq 0$ , and $S \neq 0$ , we have

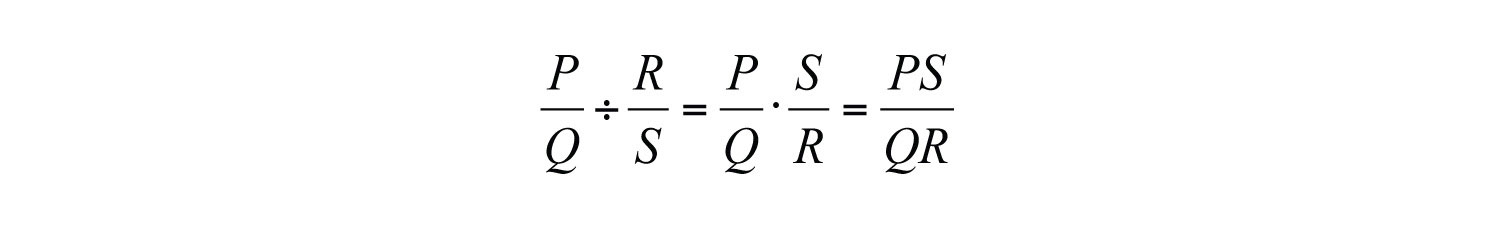
Example 8: Divide: $\frac{8 x^{5} y}{25 z^{6}} \div \frac{20 x y^{4}}{15 z^{3}}$ .

Solution: First, multiply by the reciprocal of the divisor and then cancel.

Answer: $\frac{6 x^{4}}{25 y^{3} z^{3}}$

Example 9: Divide: $\frac{x + 2}{x^{2} - 4} \div \frac{x + 3}{x - 2}$ .

Solution: After multiplying by the reciprocal of the divisor, factor and cancel.

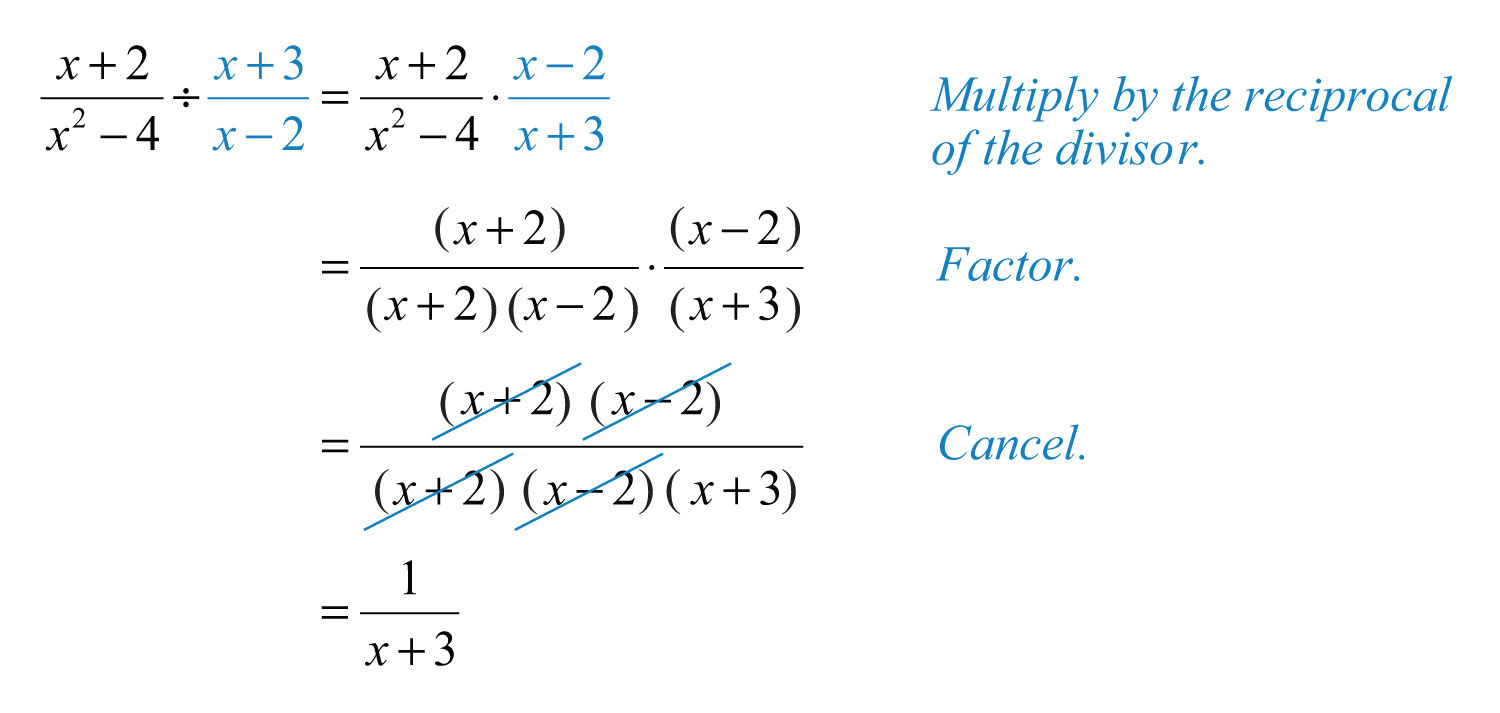
Answer: $\frac{1}{x + 3}$

Example 10: Divide: $\frac{x^{2} - 6 x - 16}{x^{2} + 4 x - 21} \div \frac{x^{2} + 9 x + 14}{x^{2} - 8 x + 15}$ .

Solution: Begin by multiplying by the reciprocal of the divisor. After doing so, factor and cancel.

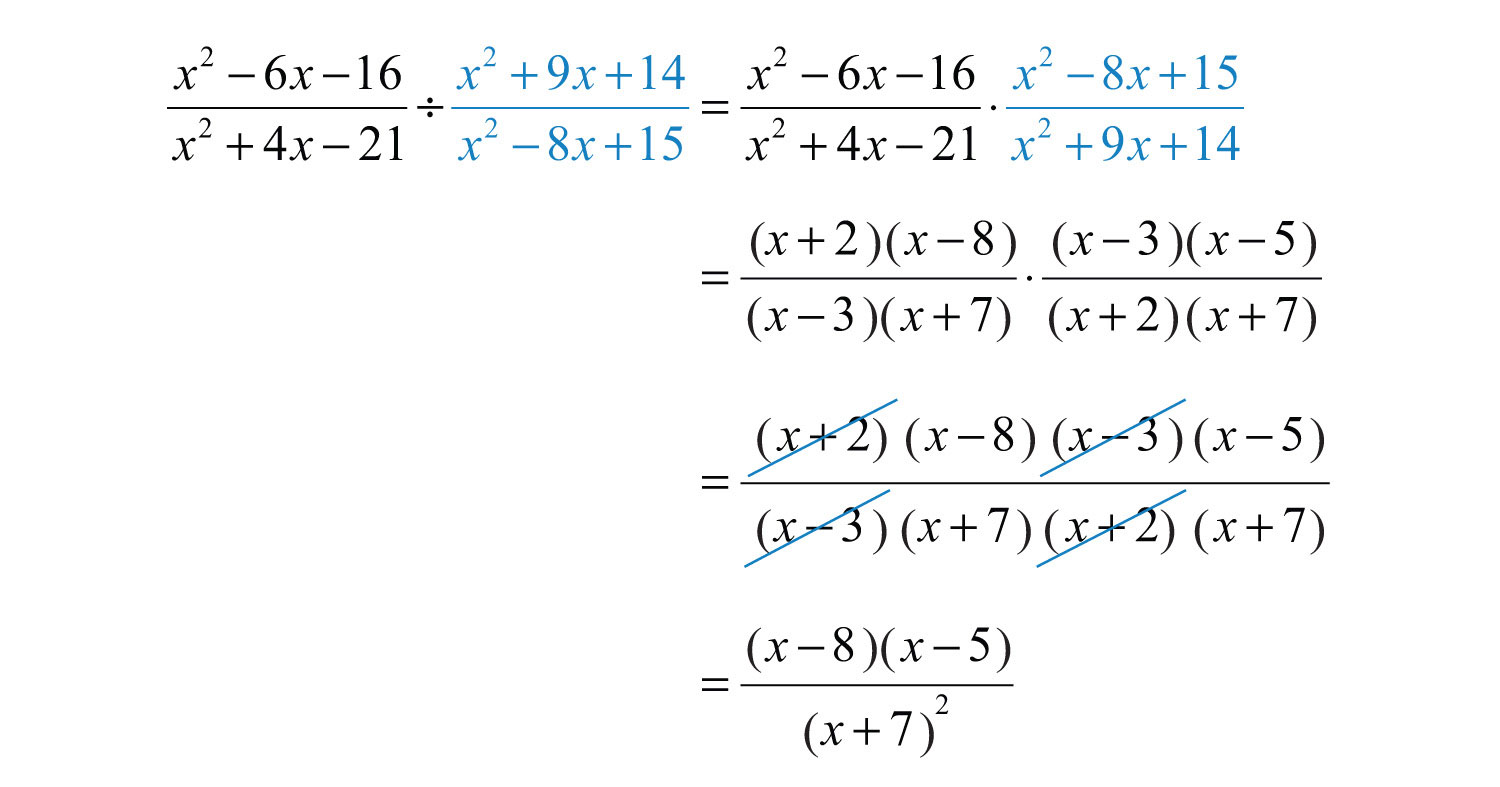
Answer: $\frac{(x - 8) (x - 5)}{{(x + 7)}^{2}}$

Example 11: Divide: $\frac{9 - 4 x^{2}}{x + 2} \div (2 x - 3)$ .

Solution: Just as we do with fractions, think of the divisor $(2 x - 3)$ as an algebraic fraction over 1.

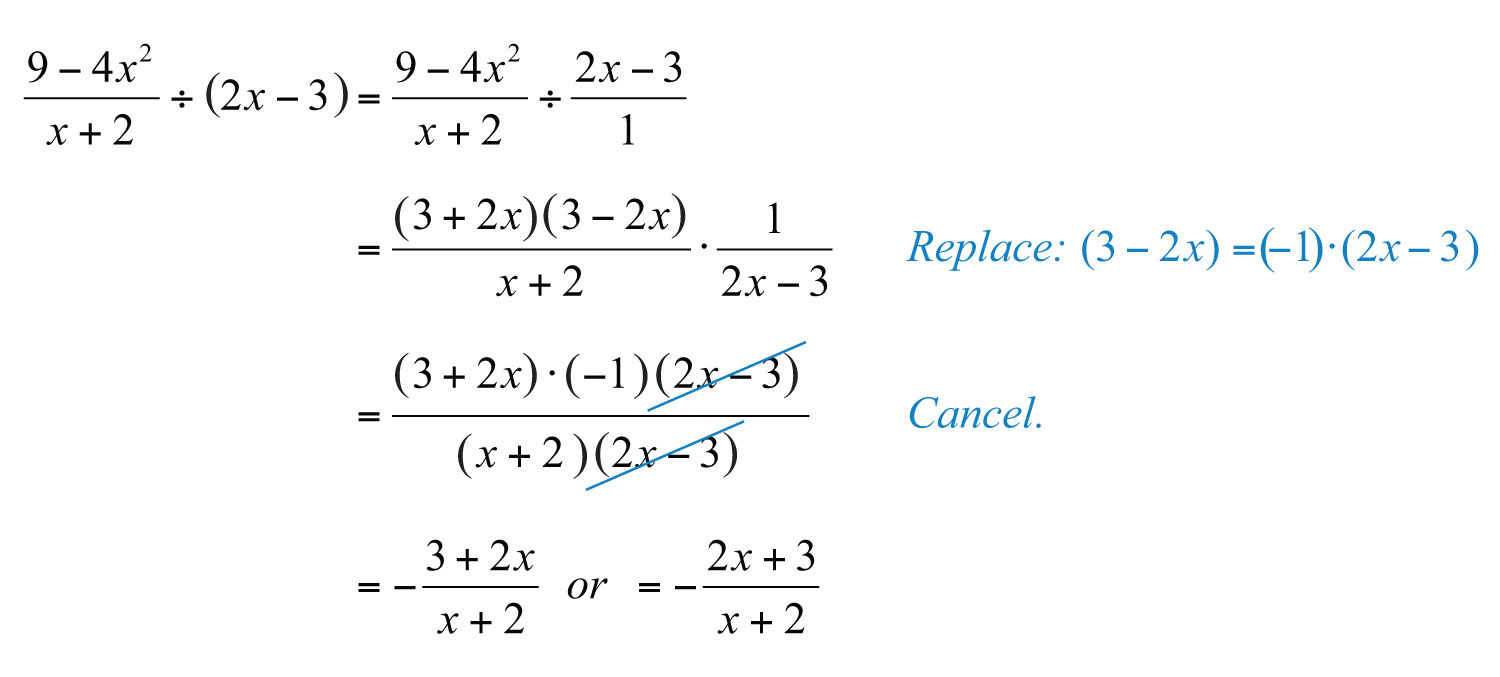
Answer: $- \frac{2 x + 3}{x + 2}$

Try this! Divide: $\frac{4 x^{2} + 7 x - 2}{25 x^{2}} \div \frac{1 - 4 x}{100 x^{4}}$ .

Answer: $- 4 x^{2} (x + 2)$

Video Solution

(click to see video)

Multiplying and Dividing Rational Functions

The product and quotient of two rational functions can be simplified using the techniques described in this section. The restrictions to the domain of a product consist of the restrictions of each function.

Example 12: Calculate $(f \cdot g) (x)$ and determine the restrictions to the domain.

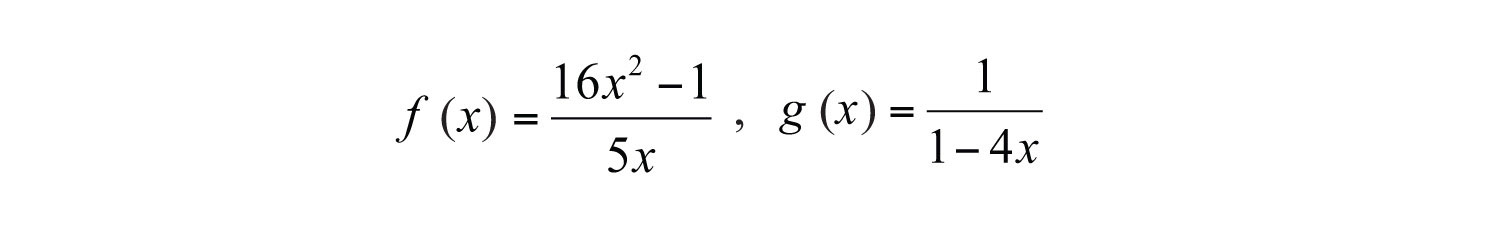
Solution: In this case, the domain of $f (x)$ consists of all real numbers except 0, and the domain of $g (x)$ consists of all real numbers except 1/4. Therefore, the domain of the product consists of all real numbers except 0 and 1/4. Multiply the functions and then simplify the result.

Answer: $(f \cdot g) (x) = - \frac{4 x + 1}{5 x}$ , where $x \neq 0, \frac{1}{4}$

The restrictions to the domain of a quotient will consist of the restrictions of each function as well as the restrictions on the reciprocal of the divisor.

Example 13: Calculate $(f / g) (x)$ and determine the restrictions.

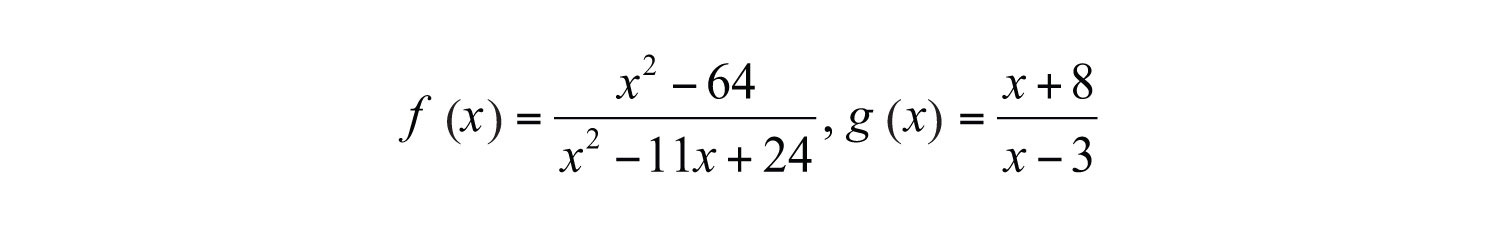
Solution:

In this case, the domain of $f (x)$ consists of all real numbers except 3 and 8, and the domain of $g (x)$ consists all real numbers except 3. In addition, the reciprocal of $g (x)$ has a restriction of −8. Therefore, the domain of this quotient consists of all real numbers except 3, 8, and −8.

Answer: $(f / g) (x) = 1$ , where $x \neq 3, 8, - 8$

Key Takeaways

After multiplying rational expressions, factor both the numerator and denominator and then cancel common factors. Make note of the restrictions to the domain. The values that give a value of 0 in the denominator are the restrictions.
To divide rational expressions, multiply by the reciprocal of the divisor.
The restrictions to the domain of a product consist of the restrictions to the domain of each factor.
The restrictions to the domain of a quotient consist of the restrictions to the domain of each rational expression as well as the restrictions on the reciprocal of the divisor.

Topic Exercises

Part A: Multiplying Rational Expressions

Multiply. (Assume all denominators are nonzero.)

1. $\frac{2 x}{3} \cdot \frac{9}{4 x^{2}}$

2. $\frac{- 5 x^{3}}{y} \cdot \frac{y^{2}}{25 x}$

3. $\frac{5 x^{2}}{2 y} \cdot \frac{4 y^{2}}{15 x^{3}}$

4. $\frac{16 a^{4}}{7 b^{2}} \cdot \frac{49 b}{32 a^{3}}$

5. $\frac{x - 6}{12 x^{3}} \cdot \frac{24 x^{2}}{x - 6}$

6. $\frac{x + 10}{2 x - 1} \cdot \frac{x - 2}{x + 10}$

7. $\frac{{(y - 1)}^{2}}{y + 1} \cdot \frac{1}{y - 1}$

8. $\frac{y^{2} - 9}{y + 3} \cdot \frac{2 y - 3}{y - 3}$

9. $\frac{2 a - 5}{a - 5} \cdot \frac{2 a + 5}{4 a^{2} - 25}$

10. $\frac{2 a^{2} - 9 a + 4}{a^{2} - 16} \cdot (a^{2} + 4 a)$

11. $\frac{2 x^{2} + 3 x - 2}{{(2 x - 1)}^{2}} \cdot \frac{2 x}{x + 2}$

12. $\frac{9 x^{2} + 19 x + 2}{4 - x^{2}} \cdot \frac{x^{2} - 4 x + 4}{9 x^{2} - 8 x - 1}$

13. $\frac{x^{2} + 8 x + 16}{16 - x^{2}} \cdot \frac{x^{2} - 3 x - 4}{x^{2} + 5 x + 4}$

14. $\frac{x^{2} - x - 2}{x^{2} + 8 x + 7} \cdot \frac{x^{2} + 2 x - 15}{x^{2} - 5 x + 6}$

15. $\frac{x + 1}{x - 3} \cdot \frac{3 - x}{x + 5}$

16. $\frac{2 x - 1}{x - 1} \cdot \frac{x + 6}{1 - 2 x}$

17. $\frac{9 + x}{3 x + 1} \cdot \frac{3}{x + 9}$

18. $\frac{1}{2 + 5 x} \cdot \frac{5 x + 2}{5 x}$

19. $\frac{100 - y^{2}}{y - 10} \cdot \frac{25 y^{2}}{y + 10}$

20. $\frac{3 y^{3}}{6 y - 5} \cdot \frac{36 y^{2} - 25}{5 + 6 y}$

21. $\frac{3 a^{2} + 14 a - 5}{a^{2} + 1} \cdot \frac{3 a + 1}{1 - 9 a^{2}}$

22. $\frac{4 a^{2} - 16 a}{4 a - 1} \cdot \frac{1 - 16 a^{2}}{4 a^{2} - 15 a - 4}$

23. $\frac{x + 9}{- x^{2} + 14 x - 45} \cdot (x^{2} - 81)$

24. $\frac{1}{2 + 5 x} \cdot (25 x^{2} + 20 x + 4)$

25. $\frac{x^{2} + x - 6}{3 x^{2} + 15 x + 18} \cdot \frac{2 x^{2} - 8}{x^{2} - 4 x + 4}$

26. $\frac{5 x^{2} - 4 x - 1}{5 x^{2} - 6 x + 1} \cdot \frac{25 x^{2} - 10 x + 1}{3 - 75 x^{2}}$

Part B: Dividing Rational Expressions

Divide. (Assume all denominators are nonzero.)

27. $\frac{5 x}{8} \div \frac{15 x^{2}}{4}$

28. $\frac{3}{8 y} \div \frac{- 15}{2 y^{2}}$

29. $\frac{\frac{5 x^{9}}{3 y^{3}}}{\frac{25 x^{10}}{9 y^{5}}}$

30. $\frac{\frac{12 x^{4} y^{2}}{21 z^{5}}}{\frac{6 x^{3} y^{2}}{7 z^{3}}}$

31. $\frac{{(x - 4)}^{2}}{30 x^{4}} \div \frac{x - 4}{15 x}$

32. $\frac{5 y^{4}}{10 {(3 y - 5)}^{2}} \div \frac{10 y^{5}}{2 {(3 y - 5)}^{3}}$

33. $\frac{x^{2} - 9}{5 x} \div (x - 3)$

34. $\frac{y^{2} - 64}{8 y} \div (8 + y)$

35. $\frac{{(a - 8)}^{2}}{2 a^{2} + 10 a} \div \frac{a - 8}{a}$

36. $24 a^{2} b^{3} (a - 2 b) \div \frac{12 a b (a - 2 b)}{5}$

37. $\frac{x^{2} + 7 x + 10}{x^{2} + 4 x + 4} \div \frac{1}{x^{2} - 4}$

38. $\frac{2 x^{2} - x - 1}{2 x^{2} - 3 x + 1} \div \frac{1}{4 x^{2} - 1}$

39. $\frac{y + 1}{y^{2} - 3 y} \div \frac{y^{2} - 1}{y^{2} - 6 y + 9}$

40. $\frac{9 - a^{2}}{a^{2} - 8 a + 15} \div \frac{2 a^{2} - 10 a}{a^{2} - 10 a + 25}$

41. $\frac{a^{2} - 3 a - 18}{2 a^{2} - 11 a - 6} \div \frac{a^{2} + a - 6}{2 a^{2} - a - 1}$

42. $\frac{\frac{y^{2} - 7 y + 10}{y^{2} + 5 y - 14}}{\frac{2 y^{2} - 9 y - 5}{y^{2} + 14 y + 49}}$

43. $\frac{\frac{6 y^{2} + y - 1}{4 y^{2} + 4 y + 1}}{\frac{3 y^{2} + 2 y - 1}{2 y^{2} - 7 y - 4}}$

44. $\frac{x^{2} - 7 x - 18}{x^{2} + 8 x + 12} \div \frac{x^{2} - 81}{x^{2} + 12 x + 36}$

45. $\frac{4 a^{2} - b^{2}}{b + 2 a} \div {(b - 2 a)}^{2}$

46. $\frac{x^{2} - y^{2}}{y + x} \div {(y - x)}^{2}$

47. $\frac{5 y^{2} (y - 3)}{4 x^{3}} \div \frac{25 y (3 - y)}{2 x^{2}}$

48. $\frac{15 x^{3}}{3 (y + 7)} \div \frac{25 x^{6}}{9 {(7 + y)}^{2}}$

49. $\frac{3 x + 4}{x - 8} \div \frac{7 x}{8 - x}$

50. $\frac{3 x - 2}{2 x + 1} \div \frac{2 - 3 x}{3 x}$

51. $\frac{{(7 x - 1)}^{2}}{4 x + 1} \div \frac{28 x^{2} - 11 x + 1}{1 - 4 x}$

52. $\frac{4 x}{{(x + 2)}^{2}} \div \frac{2 - x}{x^{2} - 4}$

53. $\frac{a^{2} - b^{2}}{a} \div {(b - a)}^{2}$

54. $\frac{{(a - 2 b)}^{2}}{2 b} \div (2 b^{2} + a b - a^{2})$

55. $\frac{x^{2} - 6 x + 9}{x^{2} + 7 x + 12} \div \frac{9 - x^{2}}{x^{2} + 8 x + 16}$

56. $\frac{2 x^{2} - 9 x - 5}{25 - x^{2}} \div \frac{1 - 4 x + 4 x^{2}}{- 2 x^{2} - 9 x + 5}$

57. $\frac{\frac{3 x^{2} - 16 x + 5}{100 - 4 x^{2}}}{\frac{9 x^{2} - 6 x + 1}{3 x^{2} + 14 x - 5}}$

58. $\frac{\frac{10 x^{2} - 25 x - 15}{x^{2} - 6 x + 9}}{\frac{9 - x^{2}}{x^{2} + 6 x + 9}}$

Recall that multiplication and division are to be performed in the order they appear from left to right. Simplify the following.

59. $\frac{1}{x^{2}} \cdot \frac{x - 1}{x + 3} \div \frac{x - 1}{x^{3}}$

60. $\frac{x - 7}{x + 9} \cdot \frac{1}{x^{3}} \div \frac{x - 7}{x}$

61. $\frac{x + 1}{x - 2} \div \frac{x}{x - 5} \cdot \frac{x^{2}}{x + 1}$

62. $\frac{x + 4}{2 x + 5} \div \frac{x - 3}{2 x + 5} \cdot \frac{x + 4}{x - 3}$

63. $\frac{2 x - 1}{x + 1} \div \frac{x - 4}{x^{2} + 1} \cdot \frac{x - 4}{2 x - 1}$

64. $\frac{4 x^{2} - 1}{3 x + 2} \div \frac{2 x - 1}{x + 5} \cdot \frac{3 x + 2}{2 x + 1}$

Part C: Multiplying and Dividing Rational Functions

Calculate $(f \cdot g) (x)$ and determine the restrictions to the domain.

65. $f (x) = \frac{1}{x}$ and $g (x) = \frac{1}{x - 1}$

66. $f (x) = \frac{x + 1}{x - 1}$ and $g (x) = x^{2} - 1$

67. $f (x) = \frac{3 x + 2}{x + 2}$ and $g (x) = \frac{x^{2} - 4}{{(3 x + 2)}^{2}}$

68. $f (x) = \frac{{(1 - 3 x)}^{2}}{x - 6}$ and $g (x) = \frac{{(x - 6)}^{2}}{9 x^{2} - 1}$

69. $f (x) = \frac{25 x^{2} - 1}{x^{2} + 6 x + 9}$ and $g (x) = \frac{x^{2} - 9}{5 x + 1}$

70. $f (x) = \frac{x^{2} - 49}{2 x^{2} + 13 x - 7}$ and $g (x) = \frac{4 x^{2} - 4 x + 1}{7 - x}$

Calculate $(f / g) (x)$ and state the restrictions.

71. $f (x) = \frac{1}{x}$ and $g (x) = \frac{x - 2}{x - 1}$

72. $f (x) = \frac{{(5 x + 3)}^{2}}{x^{2}}$ and $g (x) = \frac{5 x + 3}{6 - x}$

73. $f (x) = \frac{5 - x}{{(x - 8)}^{2}}$ and $g (x) = \frac{x^{2} - 25}{x - 8}$

74. $f (x) = \frac{x^{2} - 2 x - 15}{x^{2} - 3 x - 10}$ and $g (x) = \frac{2 x^{2} - 5 x - 3}{x^{2} - 7 x + 12}$

75. $f (x) = \frac{3 x^{2} + 11 x - 4}{9 x^{2} - 6 x + 1}$ and $g (x) = \frac{x^{2} - 2 x + 1}{3 x^{2} - 4 x + 1}$

76. $f (x) = \frac{36 - x^{2}}{x^{2} + 12 x + 36}$ and $g (x) = \frac{x^{2} - 12 x + 36}{x^{2} + 4 x - 12}$

Part D: Discussion Board Topics

77. In the history of fractions, who is credited for the first use of the fraction bar?

78. How did the ancient Egyptians use fractions?

79. Explain why $x = 7$ is a restriction to $\frac{1}{x} \div \frac{x - 7}{x - 2}$ .

Answers

1: $\frac{3}{2 x}$

3: $\frac{2 y}{3 x}$

5: $\frac{2}{x}$

7: $\frac{y - 1}{y + 1}$

9: $\frac{1}{a - 5}$

11: $\frac{2 x}{2 x - 1}$

13: −1

15: $- \frac{x + 1}{x + 5}$

17: $\frac{3}{3 x + 1}$

19: $- 25 y^{2}$

21: $- \frac{a + 5}{a^{2} + 1}$

23: $- \frac{{(x + 9)}^{2}}{x - 5}$

25: 2/3

27: $\frac{1}{6 x}$

29: $\frac{3 y^{2}}{5 x}$

31: $\frac{x - 4}{2 x^{3}}$

33: $\frac{x + 3}{5 x}$

35: $\frac{a - 8}{2 (a + 5)}$

37: $(x + 5) (x - 2)$

39: $\frac{y - 3}{y (y - 1)}$

41: $\frac{a - 1}{a - 2}$

43: $\frac{y - 4}{y + 1}$

45: $\frac{1}{2 a - b}$

47: $- \frac{y}{10 x}$

49: $- \frac{3 x + 4}{7 x}$

51: $- \frac{7 x - 1}{4 x + 1}$

53: $- \frac{a + b}{a (b - a)}$

55: $- \frac{(x - 3) (x + 4)}{{(x + 3)}^{2}}$

57: −1/4

59: $\frac{x}{x + 3}$

61: $\frac{x (x - 5)}{x - 2}$

63: $\frac{x^{2} + 1}{x + 1}$

65: $(f \cdot g) (x) = \frac{1}{x (x - 1)}$ ; $x \neq 0, 1$

67: $(f \cdot g) (x) = \frac{x - 2}{3 x + 2}$ ; $x \neq - 2, - \frac{2}{3}$

69: $(f \cdot g) (x) = \frac{(x - 3) (5 x - 1)}{x + 3}$ ; $x \neq - 3, - \frac{1}{5}$

71: $(f / g) (x) = \frac{x - 1}{x (x - 2)}$ ; $x \neq 0, 1, 2$

73: $(f / g) (x) = - \frac{1}{(x - 8) (x + 5)}$ ; $x \neq \pm 5, 8$

75: $(f / g) (x) = \frac{(x + 4)}{(x - 1)}$ ; $x \neq \frac{1}{3}, 1$