This is “General Guidelines for Factoring Polynomials”, section 6.5 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
6.5 General Guidelines for Factoring Polynomials
Learning Objective
- Develop a general strategy for factoring polynomials.
General Factoring Strategy
We have learned various techniques for factoring polynomials with up to four terms. The challenge is to identify the type of polynomial and then decide which method to apply. The following outlines a general guideline for factoring polynomials:
- Check for common factors. If the terms have common factors, then factor out the greatest common factor (GCF) and look at the resulting polynomial factors to factor further.
-
Determine the number of terms in the polynomial.
a. Factor four-term polynomials by grouping.
b. Factor trinomials (three terms) using “trial and error” or the AC method.
c. Factor binomials (two terms) using the following special products:
Difference of squares: Sum of squares: Difference of cubes: Sum of cubes: - Look for factors that can be factored further.
- Check by multiplying.
Note
- If a binomial is both a difference of squares and a difference of cubes, then first factor it as difference of squares and then as a sum and difference of cubes to obtain a more complete factorization.
- Not all polynomials with integer coefficients factor. When this is the case, we say that the polynomial is prime.
If an expression has a GCF, then factor this out first. Doing so is often overlooked and typically results in factors that are easier to work with. Also, look for the resulting factors to factor further; many factoring problems require more than one step. A polynomial is completely factored when none of the factors can be factored further.
Example 1: Factor: .
Solution: This four-term polynomial has a GCF of . Factor this out first.
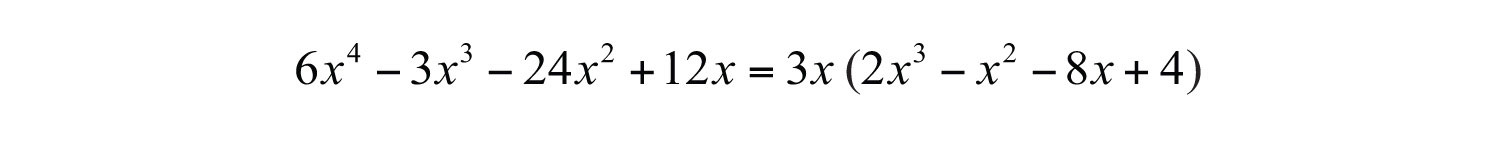
Now factor the resulting four-term polynomial by grouping.
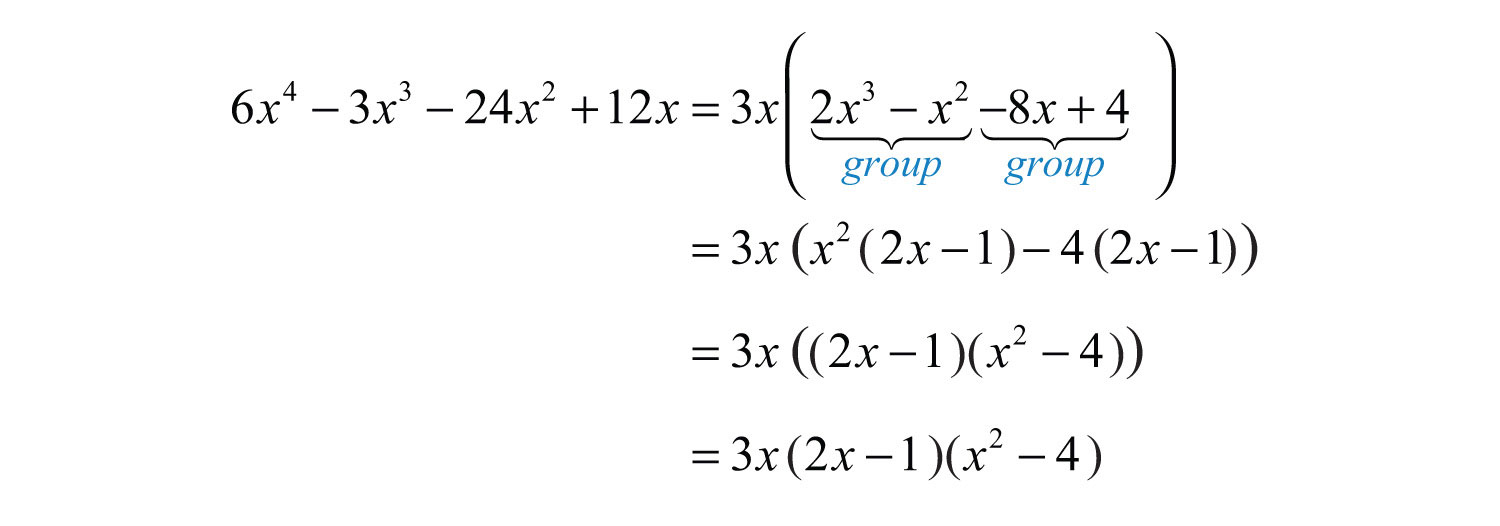
The factor is a difference of squares and can be factored further.
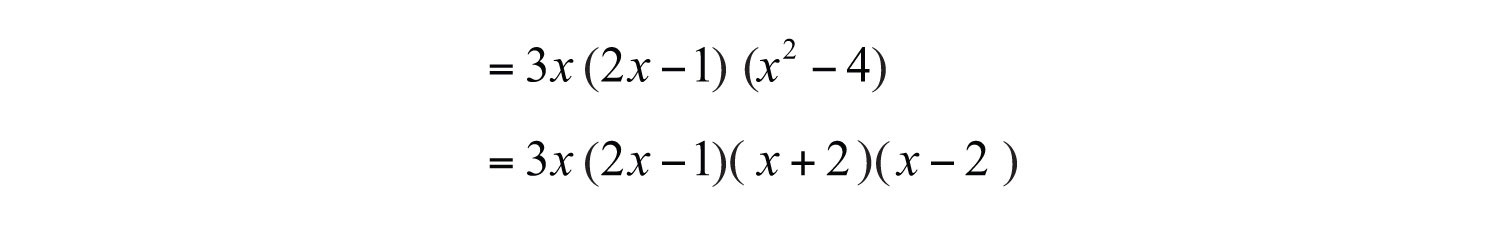
Answer:
Example 2: Factor: .
Solution: This trinomial has a GCF of . Factor this out first.
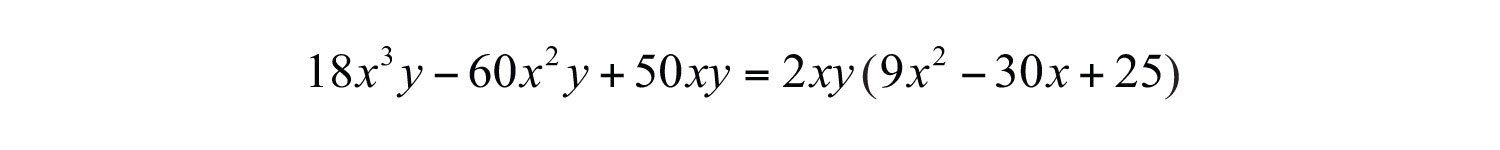
The trinomial factor can be factored further using the trial and error method. Use the factors and . These combine to generate the correct coefficient for the middle term: .

Check.

Answer:
Example 3: Factor: .
Solution: This trinomial has a GCF of . Factor this out first.
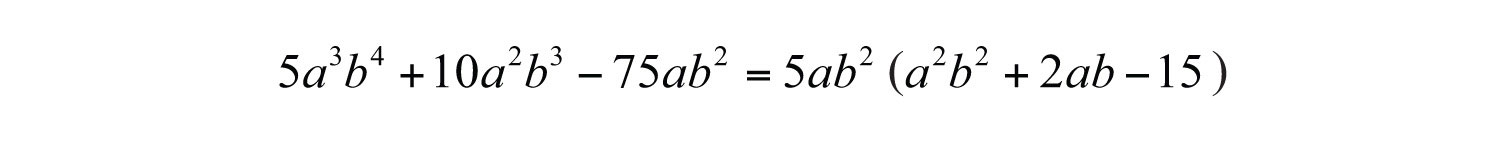
The resulting trinomial factor can be factored as follows:
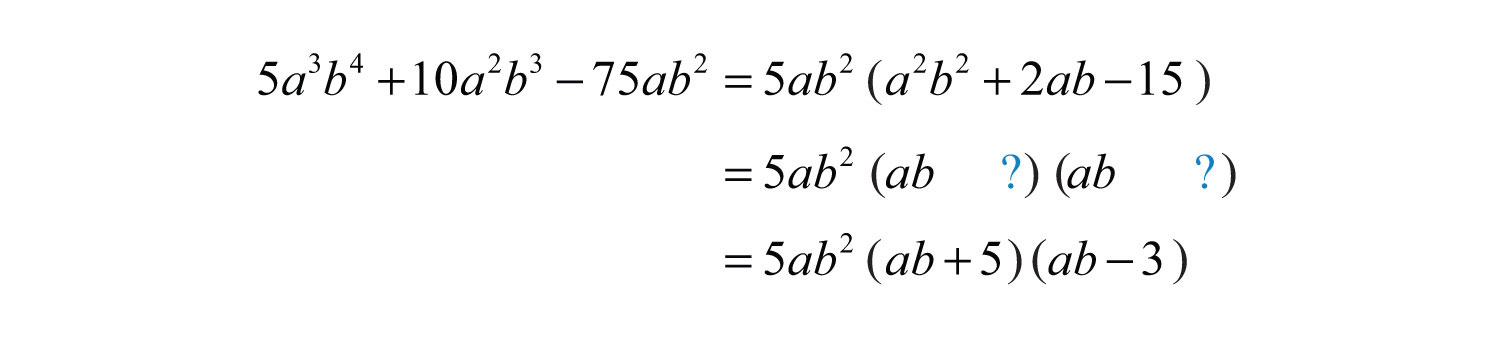
Answer:
Try this! Factor: .
Answer:
Video Solution
(click to see video)
Example 4: Factor: .
Solution: This binomial does not have a GCF. Therefore, begin factoring by identifying it as a difference of squares.
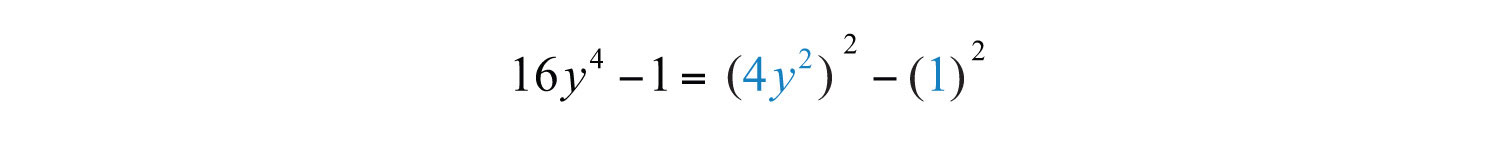
Here and b = 1. Substitute into the formula for difference of squares.
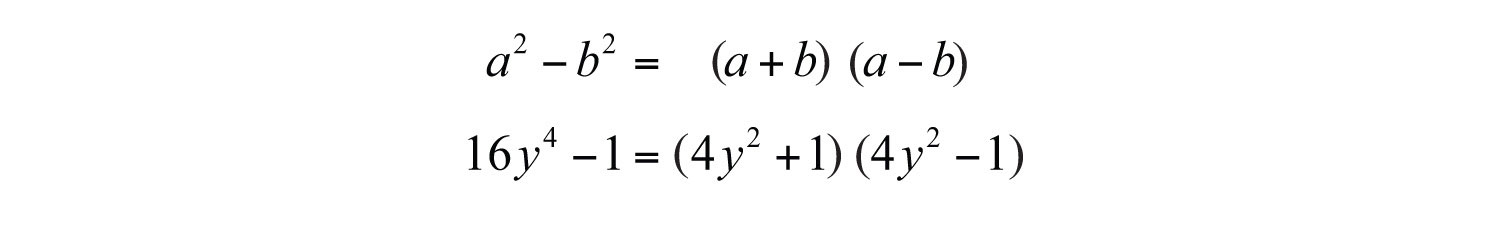
The factor is a sum of squares and is prime. However, is a difference of squares and can be factored further.
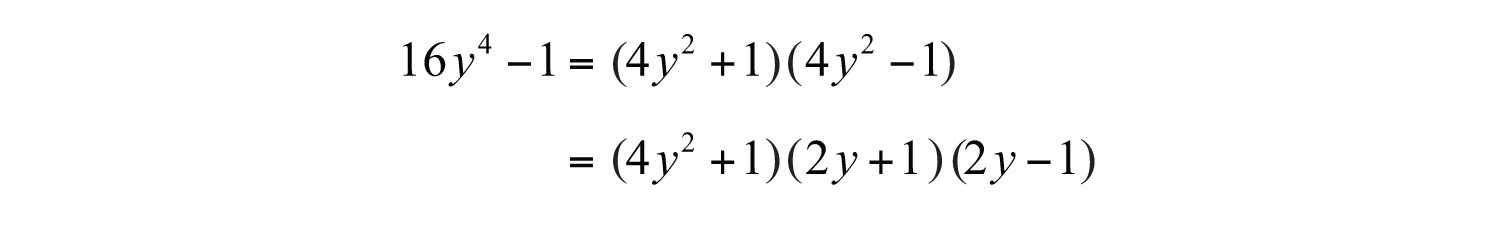
Answer:
Example 5: Factor: .
Solution: This binomial is a difference of squares and a difference of cubes. When this is the case, first factor it as a difference of squares.

We can write

Each factor can be further factored either as a sum or difference of cubes, respectively.
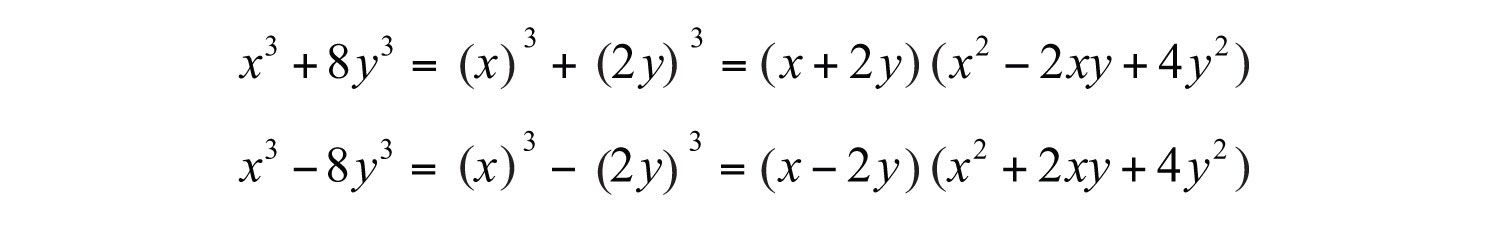
Therefore,
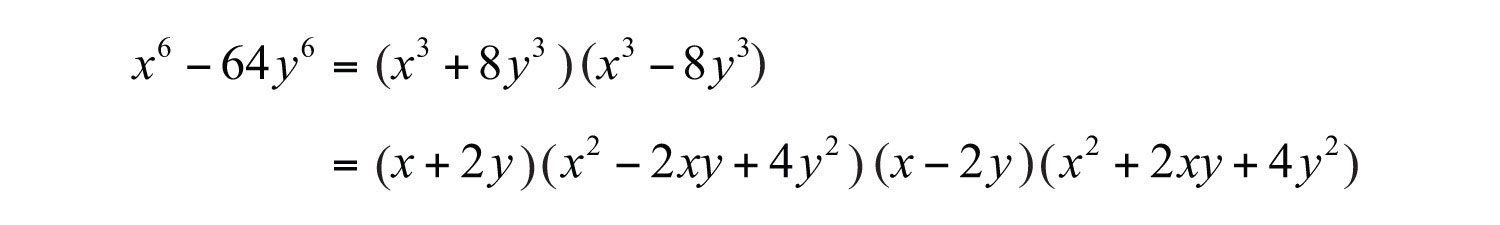
Answer:
Example 6: Factor: .
Solution: First, identify this expression as a difference of squares.
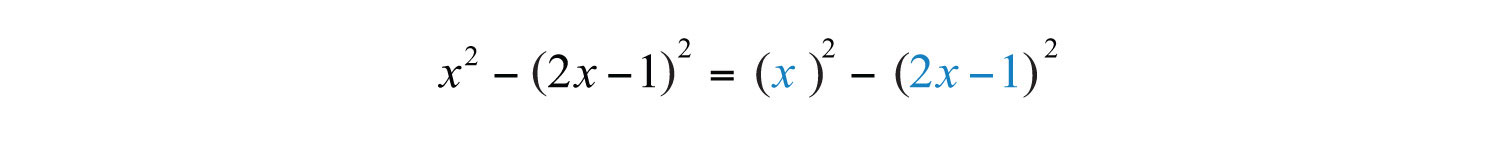
Here use and in the formula for a difference of squares.
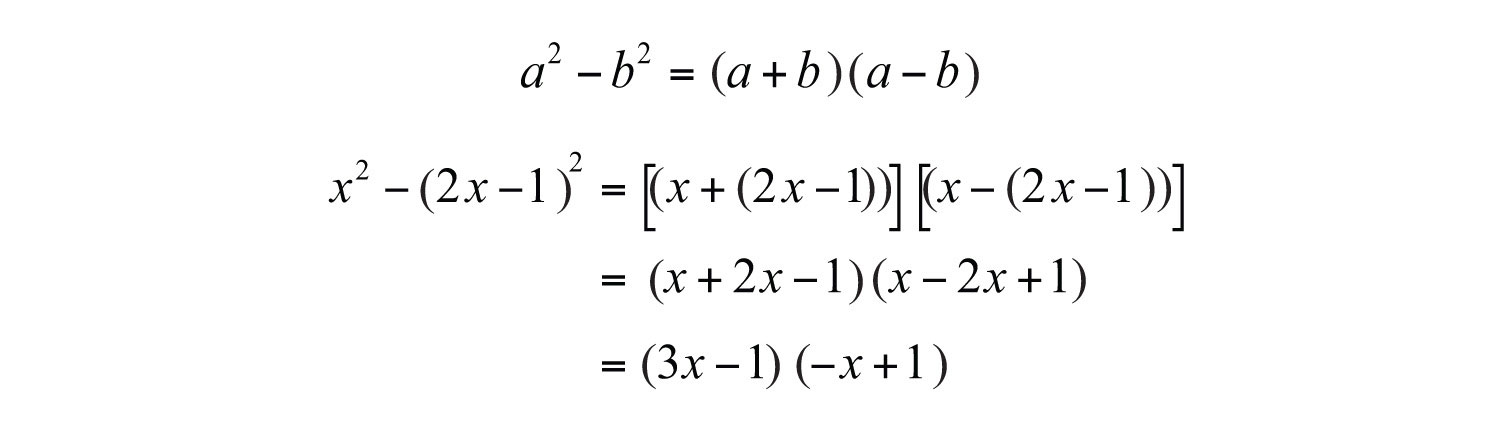
Answer:
Try this! Factor: .
Answer:
Video Solution
(click to see video)Key Takeaways
- Use the polynomial type to determine the method used to factor it.
- It is a best practice to look for and factor out the greatest common factor (GCF) first. This will facilitate further factoring and simplify the process. Be sure to include the GCF as a factor in the final answer.
- Look for resulting factors to factor further. It is often the case that factoring requires more than one step.
- If a binomial can be considered as both a difference of squares and a difference of cubes, then first factor it as a difference of squares. This results in a more complete factorization.
Topic Exercises
Part A: Mixed Factoring
Factor completely.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69. The volume of a certain rectangular solid is given by the function . Write the function in its factored form.
70. The volume of a certain right circular cylinder is given by the function . Write the function in its factored form.
Part B: Discussion Board
71. First, factor the trinomial . Then factor out the GCF. Discuss the significance of factoring out the GCF first. Do you obtain the same result?
72. Discuss a plan for factoring polynomial expressions on an exam. What should you be looking for and what should you be expecting?
Answers
1:
3:
5:
7:
9:
11:
13:
15:
17:
19: Prime
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41: Prime
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:




