This is “Review of Decimals and Percents”, section 1.5 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
1.5 Review of Decimals and Percents
Learning Objectives
- Convert fractions to decimals and back.
- Perform operations with decimals.
- Round off decimals to a given place.
- Define a percent.
- Convert percents to decimals and back.
- Convert fractions to percents and back.
Decimals
In this section, we provide a brief review of the decimal system. A real number in decimal form, a decimalA real number expressed using the decimal system. consists of a decimal point, digits (0 through 9) to the left of the decimal point representing the whole number part, and digits to the right of the decimal point representing the fractional part. The digits represent powers of 10 as shown in the set {…, 1,000, 100, 10, 1, 1/10, 1/100, 1/1,000, …} according to the following diagram:
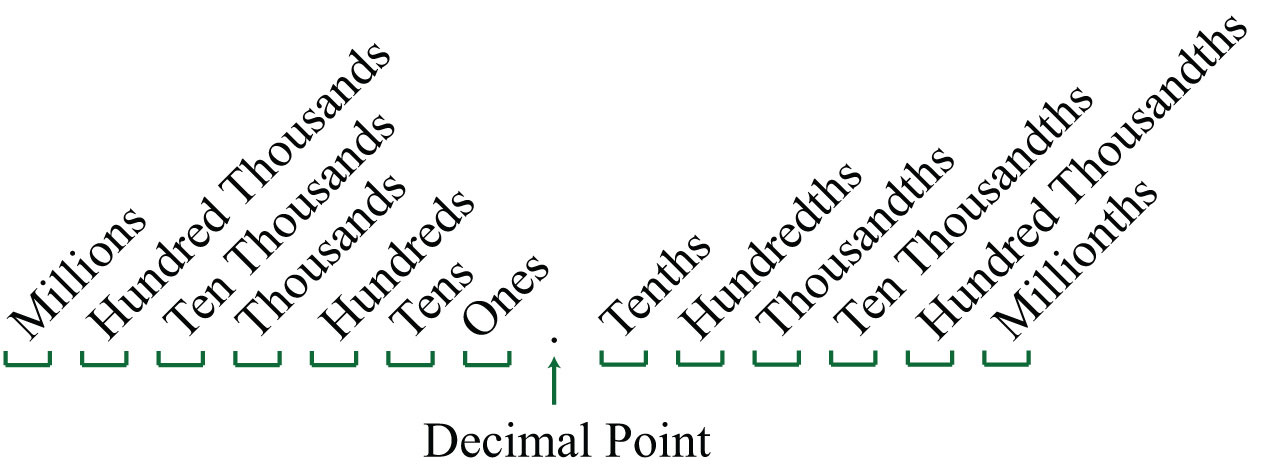
For example, the decimal 538.3 can be written in the following expanded form:
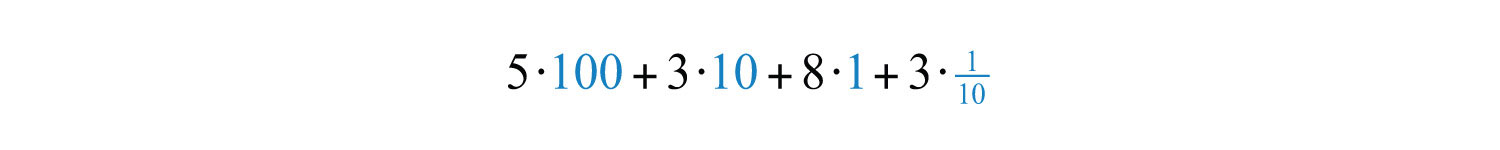
After simplifying, we obtain the mixed number . Use this process to convert decimals to mixed numbers.
Example 1: Write as a mixed number: 32.15.
Solution: In this example, 32 is the whole part and the decimal ends in the hundredths place. Therefore, the fractional part will be 15/100, and we can write
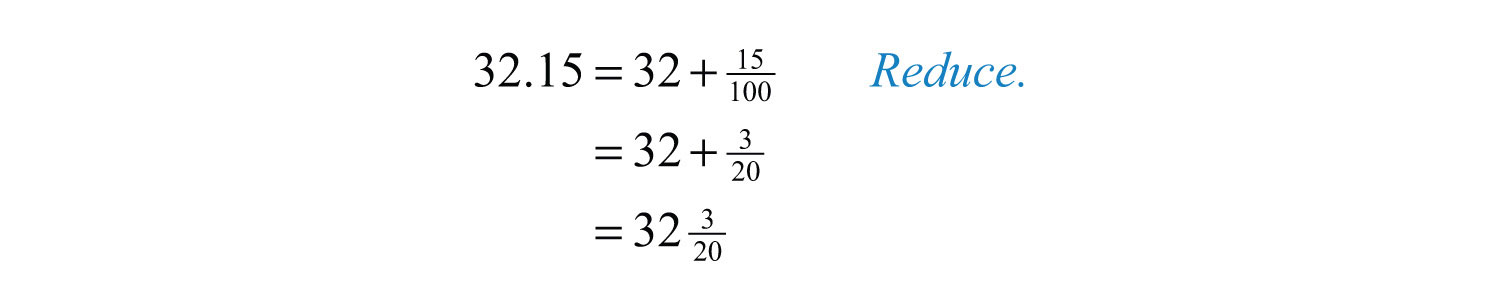
Answer:
To convert fractions to decimal equivalents, divide.
Example 2: Write as a decimal: .
Solution: Use long division to convert to a decimal.
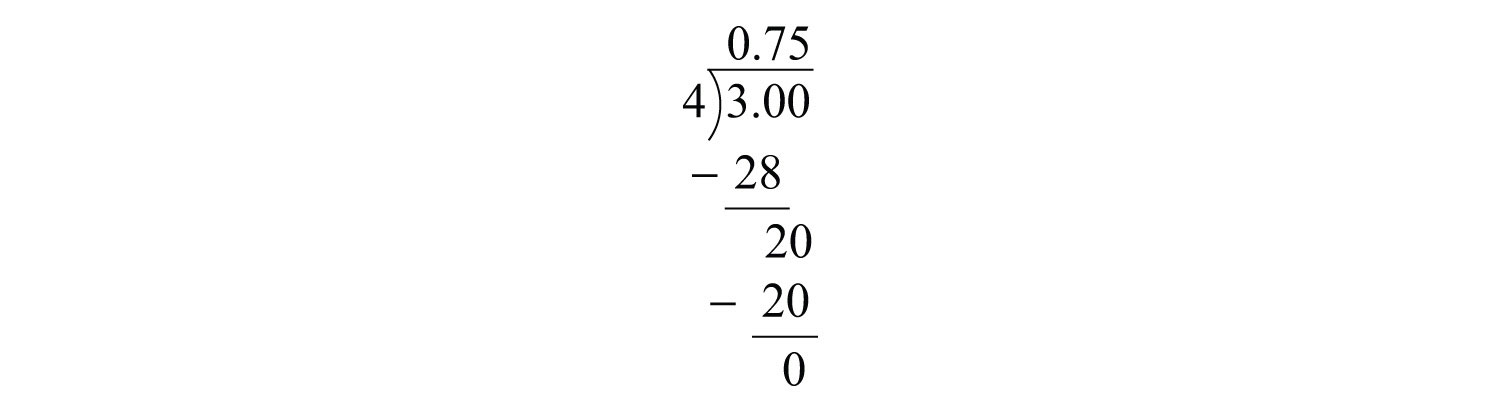
Answer:
If the division never ends, then use a bar over the repeating digit (or block of digits) to indicate a repeating decimal.
Example 3: Write as a decimal: .
Solution: Use long division to convert the fractional part to a decimal and then add the whole part.
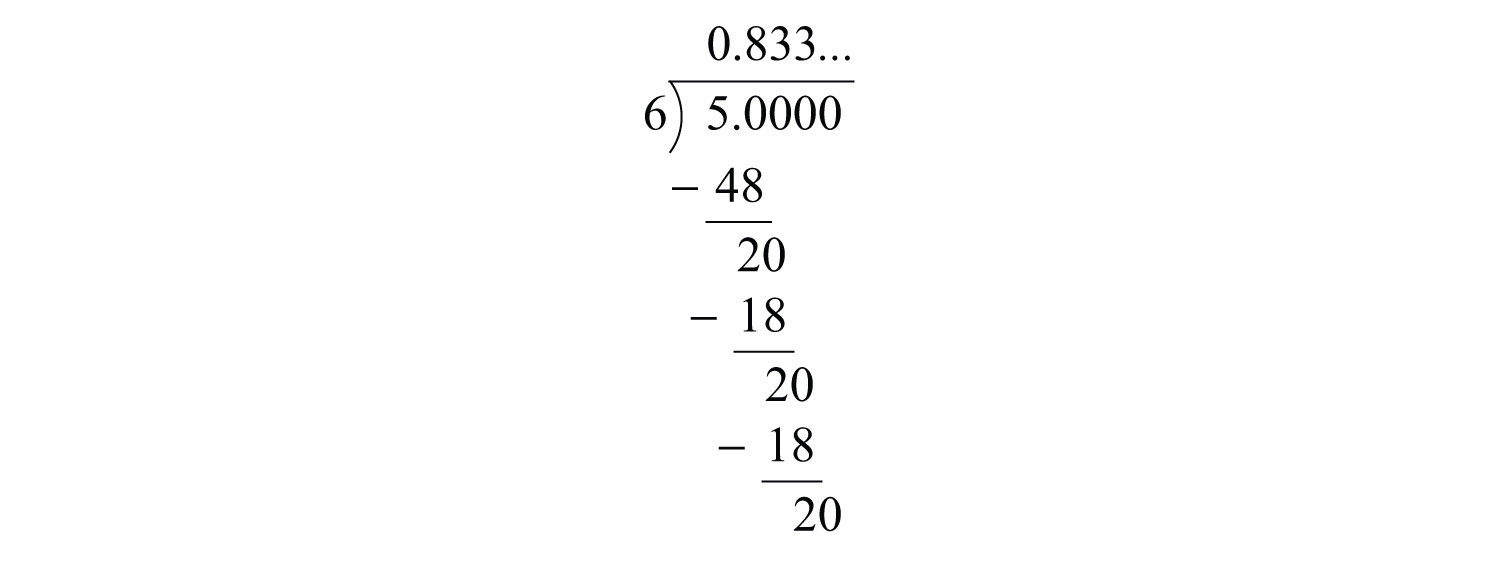
At this point, we can see that the long division will continue to repeat. When this is the case, use a bar over the repeating digit to indicate that it continues forever:
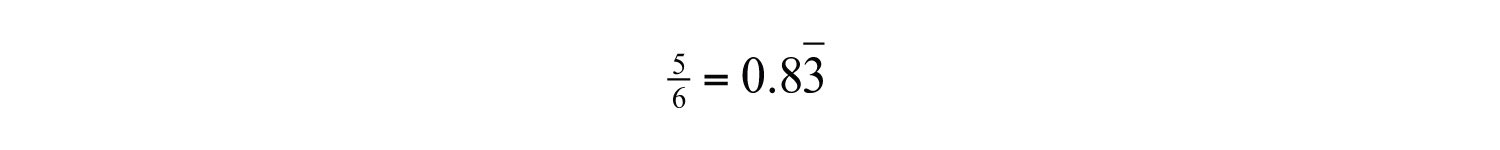
Then write
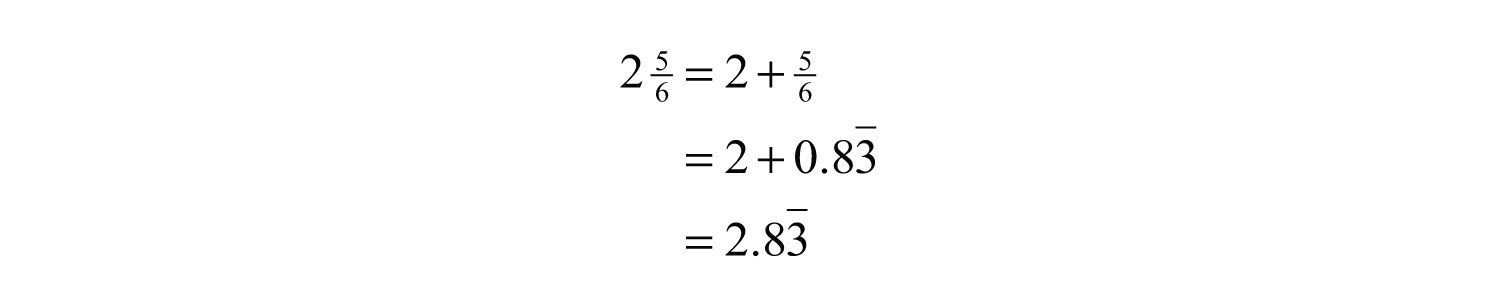
Answer:
To add or subtract decimals, align them vertically with the decimal point and add corresponding place values. Recall that sometimes you need to borrow from or carry over to the adjoining column (regrouping).
Example 4: Subtract: .
Solution: Note that trailing zeros to the right of the decimal point do not change the value of the decimal, 23.25 = 23.250. In this case, you need to borrow from the tenths place (regroup) to subtract the digits in the hundredths place.
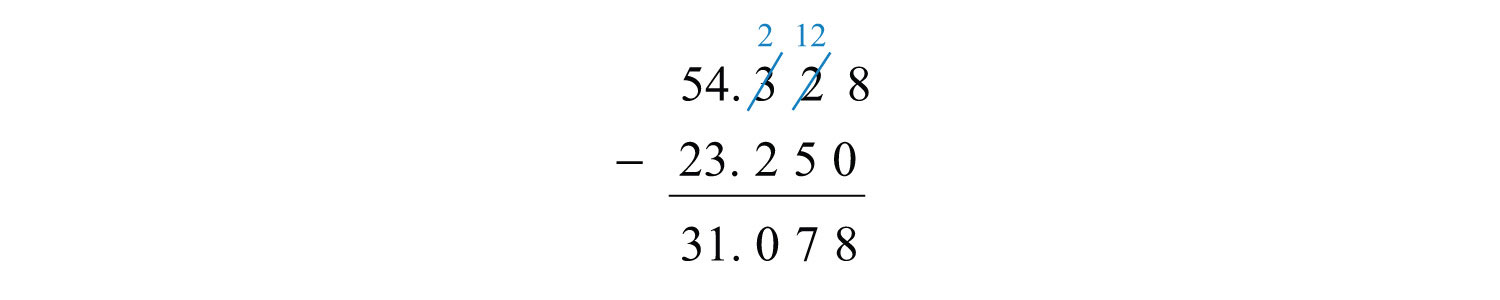
Answer: 31.078
Multiply decimals the same way you multiply whole numbers. The number of decimal places in the product will be the sum of the decimal places found in each of the factors.
Example 5: Multiply: .
Solution: The total number of decimal places of the two factors is 2 + 1 = 3. Therefore, the result has 3 decimal places.

Answer: 39.664
When dividing decimals, move the decimal points of both the dividend and the divisor so that the divisor is a whole number. Remember to move the decimal the same number of places for both the dividend and divisor.
Example 6: Divide: .
Solution: Move the decimal point to turn the divisor into a whole number: 624. Move the decimal points of both the divisor and dividend two places to the right.

Next, divide.
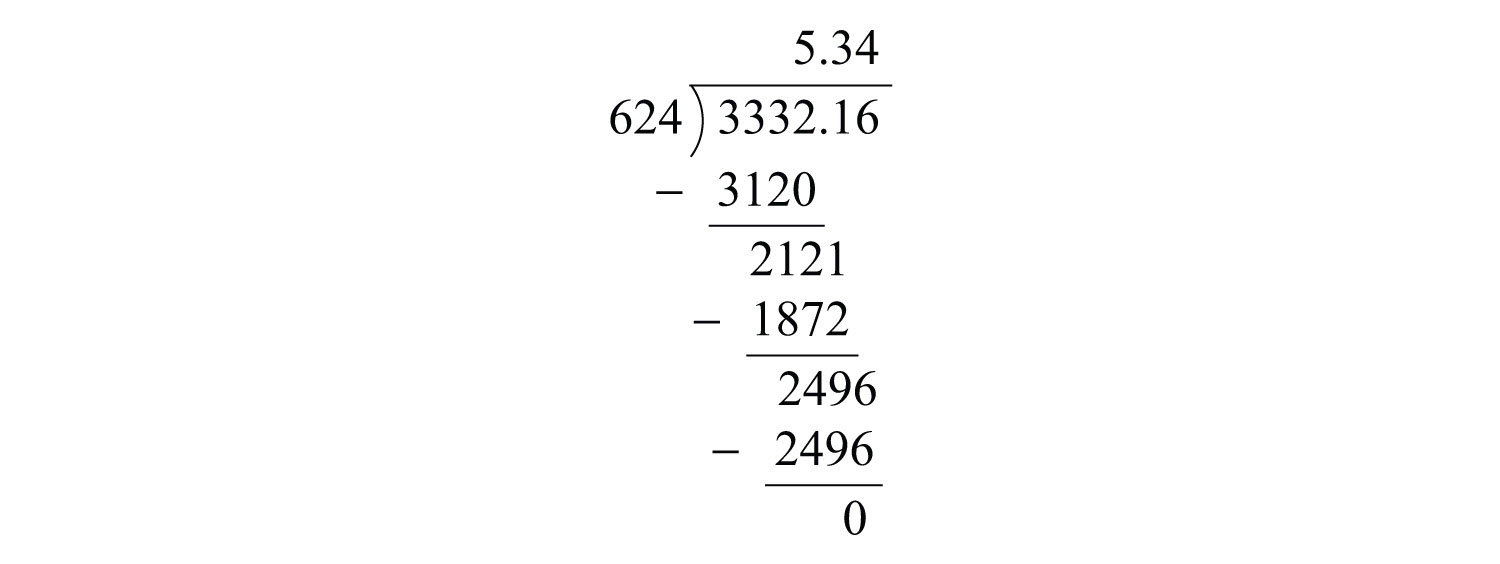
Answer: 5.34
It is often necessary to round offA means of approximating decimals with a specified number of significant digits. decimals to a specified number of decimal places. Rounding off allows us to approximate decimals with fewer significant digits. To do this, look at the digit to the right of the specified place value.
- If the digit to the right of the specified place is 4 or less, then leave the specified digit unchanged and drop all subsequent digits.
- If the digit to the right of the specified place is 5 or greater, then increase the value of the digit in the specified place by 1 and drop all subsequent digits.
Recall that decimals with trailing zeros to the right of the decimal point can be dropped. For example, round 5.635457 to the nearest thousandth:

Round the same number 5.635457 to the nearest hundredth:

After rounding off, be sure to use the appropriate notation ( ) to indicate that the number is now an approximation. When working with US currency, we typically round off to two decimal places, or the nearest hundredth.
Example 7: Calculate and round off to the nearest hundredth.
a. 1/3 of $10.25.
b. 1/4 of $10.25.
Solution: In this context, the key word “of” indicates that we should multiply.
a. Multiplying by is equivalent to dividing by 3.
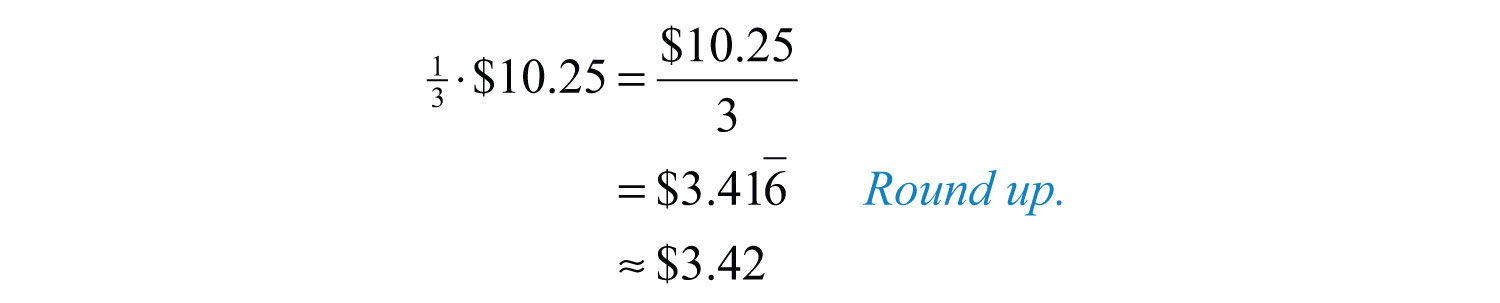
b. Multiplying by is equivalent to dividing by 4.
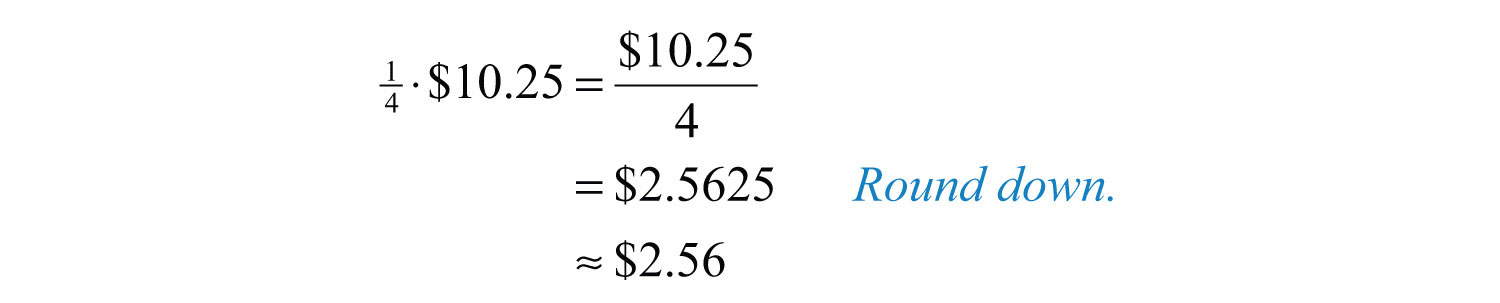
Answers: a. $3.42; b. $2.56
Definition of Percent
A percentA representation of a number as part of 100: . is a representation of a number as a part of one hundred. The word “percent” can be written “per cent” which means “per 100” or “/100.” We use the symbol ( % ) to denote a percentage:
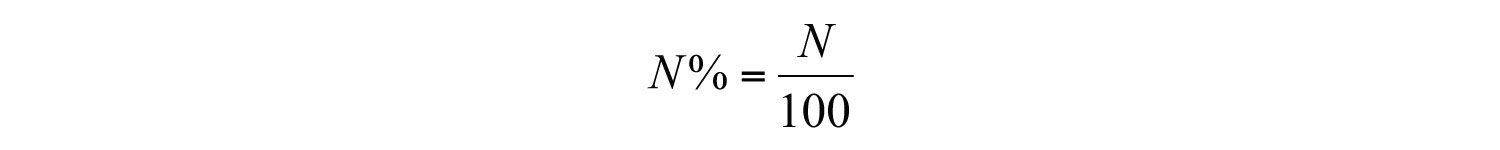
For example,
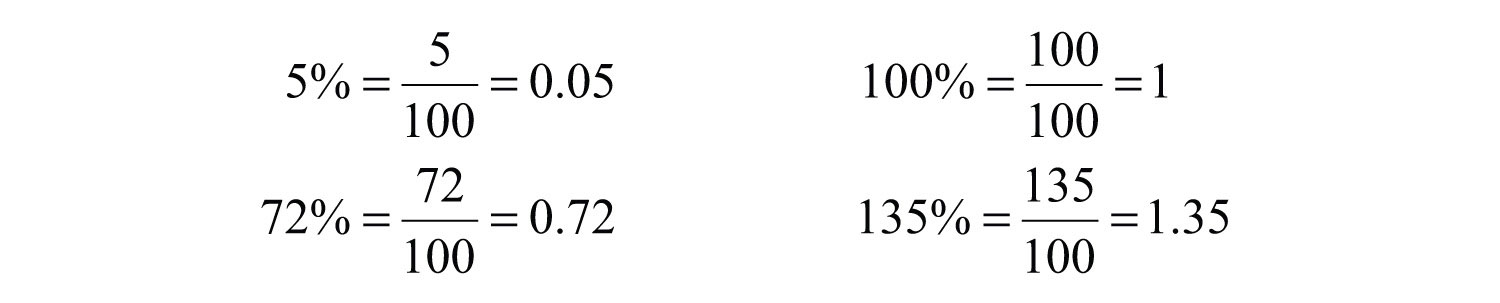
Percents are an important part of our everyday life and show up often in our study of algebra. Percents can be visualized using a pie chartA circular graph divided into sectors whose area is proportional to the relative size of the ratio of the part to the total. (or circle graph), where each sector gives a visual representation of a percentage of the whole. For example, the following pie chart shows the percentage of students in certain age categories of all US community colleges.
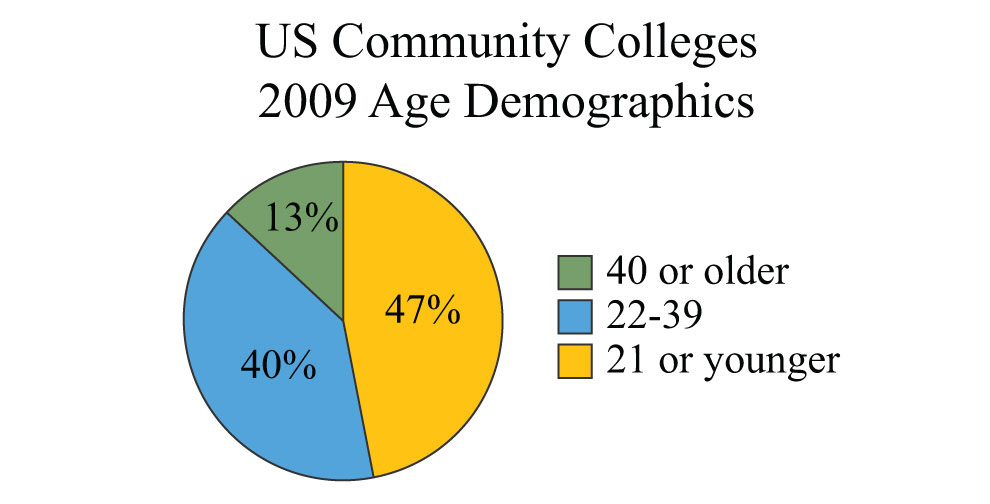
Source: American Association of Community Colleges.
Each sector is proportional to the size of the part out of the whole. The sum of the percentages presented in a pie chart must be 100%. To work with percentages effectively, you have to know how to convert percents to decimals or fractions and back again.
Percents to Decimals
Applying the definition of percent, you see that . The same result can be obtained by moving the decimal two places to the left. To convert percents to decimals, either apply the definition or move the decimal two places to the left.
Example 8: Convert to a decimal: 152%.
Solution: Treat and move the decimal two places to the left.
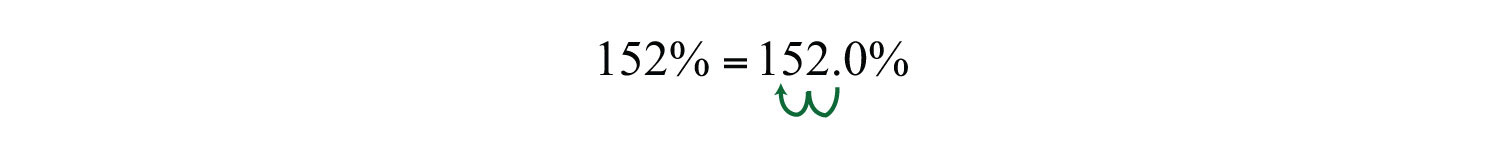
Answer: 1.52
Example 9: Convert to a decimal: .
Solution: First, write the decimal percent equivalent,
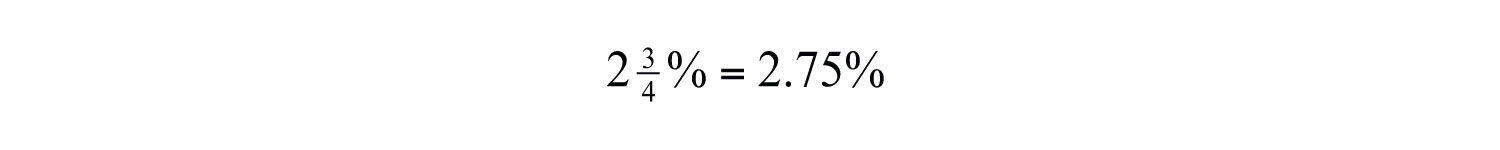
Next, move the decimal two places to the left,

At this point, fill in the tenths place with a zero.
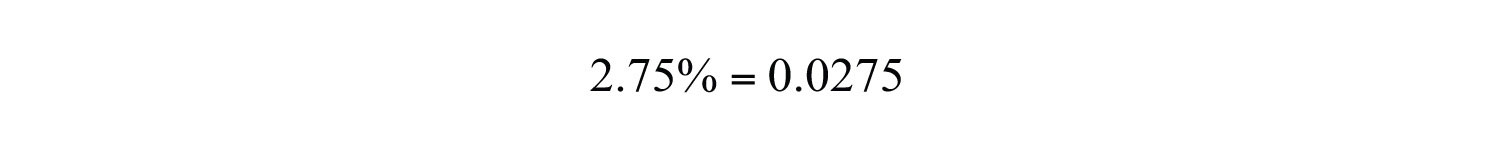
Answer: 0.0275
Try this! Convert to a decimal: 215%.
Answer: 2.15
Video Solution
(click to see video)Decimals and Fractions to Percents
To convert a decimal to a percent, convert the decimal to a fraction of 100 and apply the definition of percent, or equivalently, move the decimal to the right two places and add a percent sign.
Example 10: Convert 0.23 to a percent.
Solution: First, convert the decimal to a fraction of 100 and apply the definition.
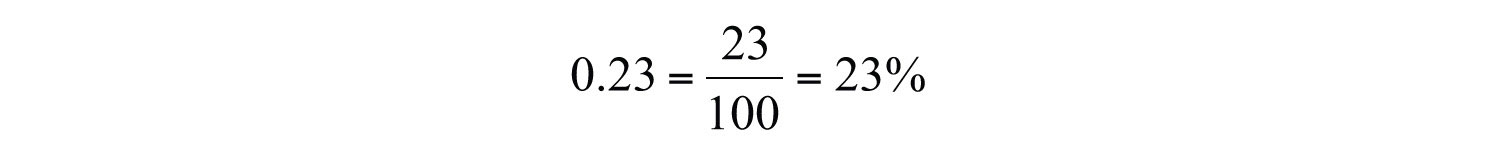
You can achieve the same result by moving the decimal two places to the right and adding a percent sign.
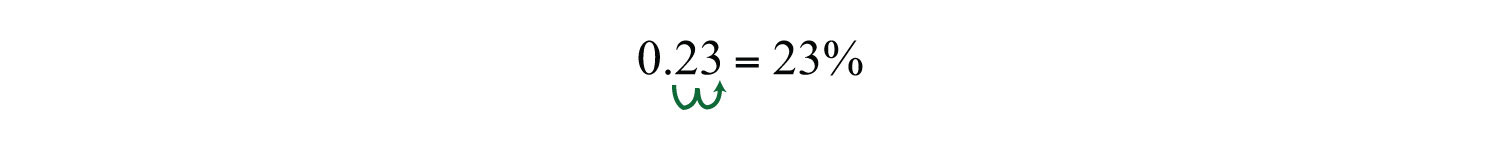
Answer: 23%.
Alternatively, you can multiply by 1 in the form of 100%.
Example 11: Convert 2.35 to a percent.
Solution: Recall that 1 = 100%.
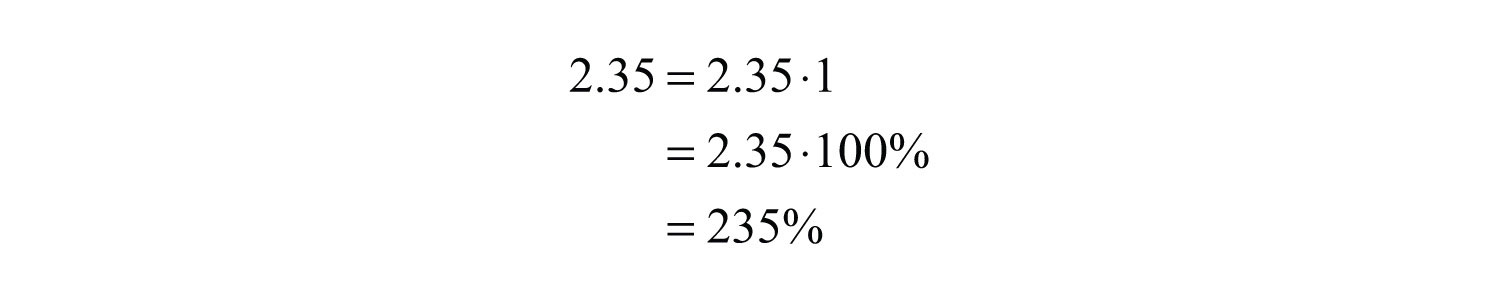
You can achieve the same result by moving the decimal two places to the right and adding a percent sign.
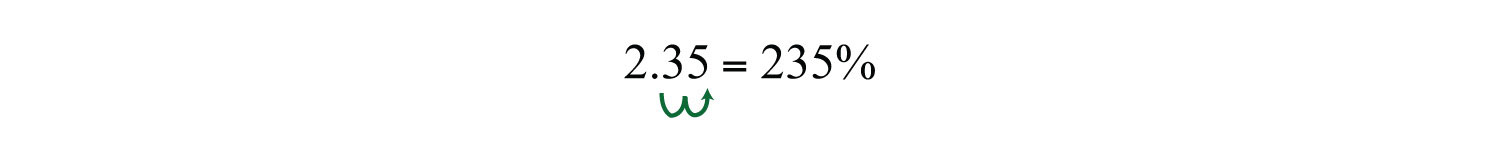
Answer: 235%
Example 12: Convert to a percent.
Solution:
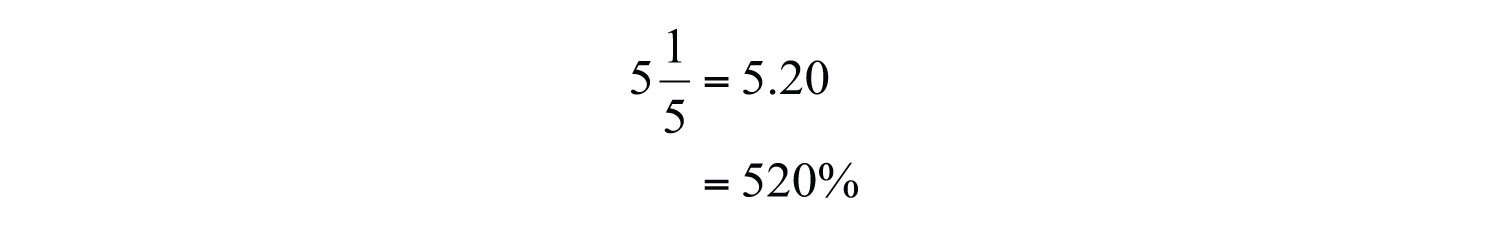
Answer: 520%
Sometimes we can use the definition of percent and find an equivalent fraction with a denominator of 100.
Example 13: Convert to a percent.
Solution: Notice that the denominator 25 is a factor of 100. Use the definition of percent by finding an equivalent fraction with 100 in the denominator.
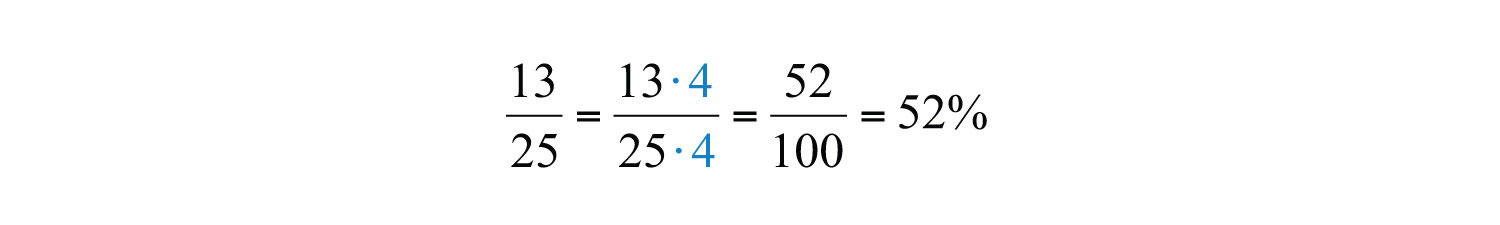
Answer: 52%
This is a very specialized technique because 100 may not be a multiple of the denominator.
Example 14: Convert to a percent.
Solution: Notice that the denominator 3 is not a factor of 100. In this case, it is best to multiply by 1 in the form of 100%.
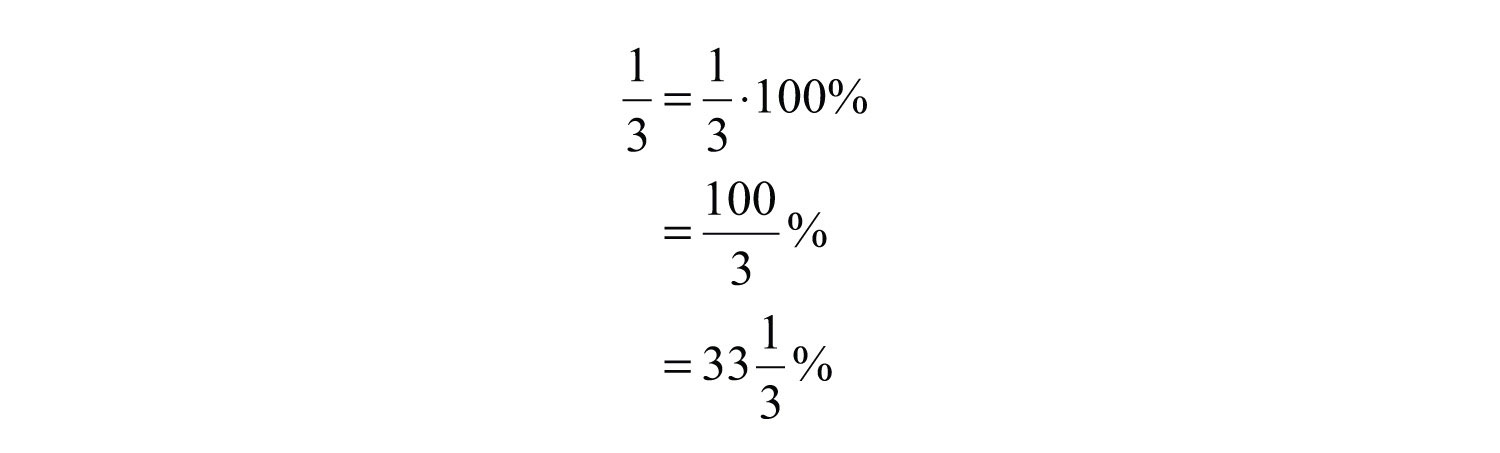
Answer:
Try this! Convert to a percent: .
Answer:
Video Solution
(click to see video)Percents to Fractions
When converting percents to fractions, apply the definition of percent and then reduce.
Example 15: Convert to a fraction: .
Solution:
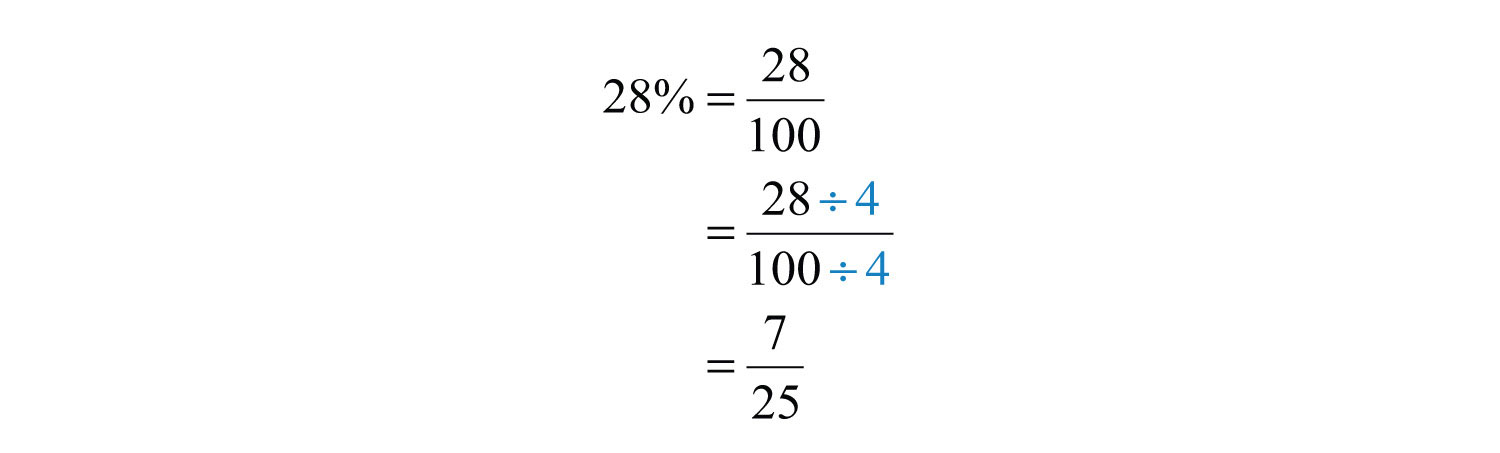
Answer:
Applying the definition of percent is equivalent to removing the percent sign and multiplying by .
Example 16: Convert to a fraction: .
Solution: First, convert to an improper fraction and then apply the definition of percent.
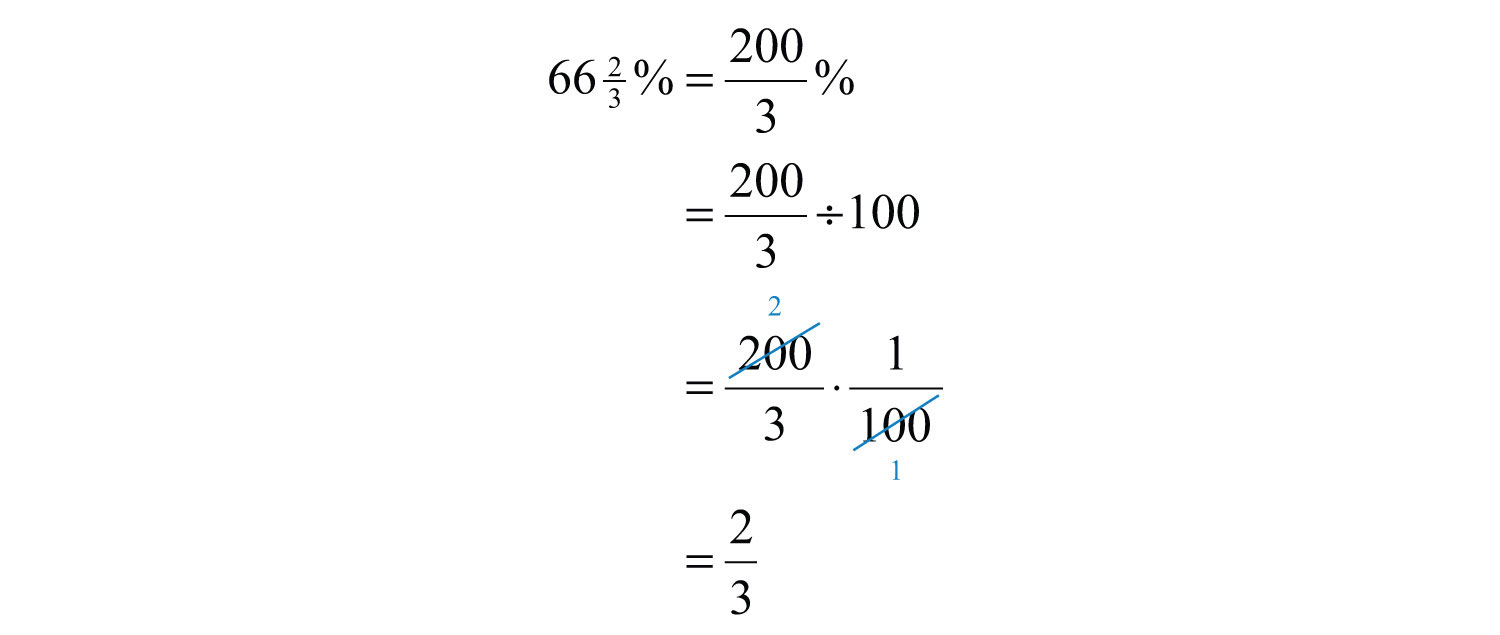
Answer:
Try this! Convert to a fraction: .
Answer:
Video Solution
(click to see video)
Example 17: Using the given pie chart, calculate the total number of students that were 21 years old or younger if the total US community college enrollment in 2009 was 11.7 million.
Solution: From the pie chart we can determine that 47% of the total 11.7 million students were 21 years old or younger.
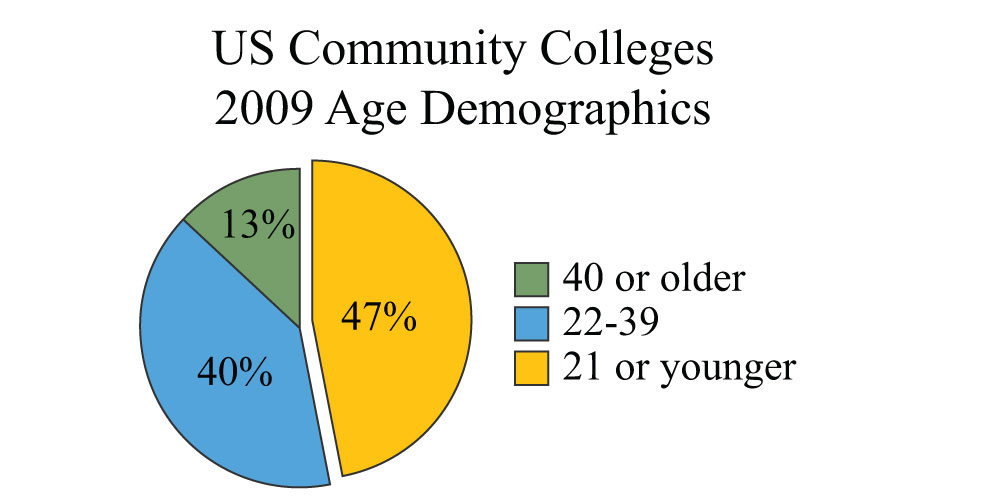
Source: American Association of Community Colleges.
Convert 47% to a decimal and multiply as indicated by the key word “of.”
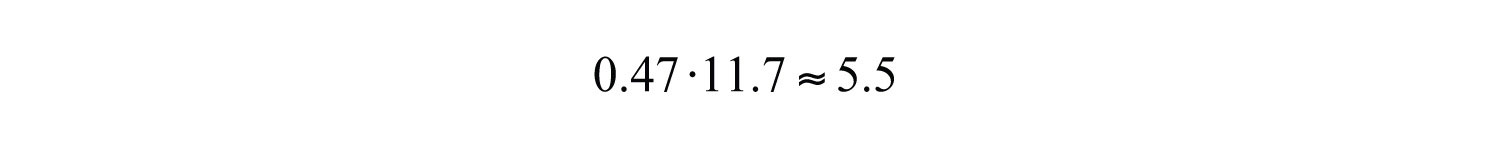
Answer: In 2009, approximately 5.5 million students enrolled in US community colleges were 21 years old or younger.
Key Takeaways
- To convert a decimal to a mixed number, add the appropriate fractional part indicated by the digits to the right of the decimal point to the whole part indicated by the digits to the left of the decimal point and reduce if necessary.
- To convert a mixed number to a decimal, convert the fractional part of the mixed number to a decimal using long division and then add it to the whole number part.
- To add or subtract decimals, align them vertically with the decimal point and add corresponding place values.
- To multiply decimals, multiply as usual for whole numbers and count the number of decimal places of each factor. The number of decimal places in the product will be the sum of the decimal places found in each of the factors.
- To divide decimals, move the decimal in both the divisor and dividend until the divisor is a whole number and then divide as usual.
- When rounding off decimals, look to the digit to the right of the specified place value. If the digit to the right is 4 or less, round down by leaving the specified digit unchanged and dropping all subsequent digits. If the digit to the right is 5 or more, round up by increasing the specified digit by one and dropping all subsequent digits.
- A percent represents a number as part of 100: .
- To convert a percent to a decimal, apply the definition of percent and write that number divided by 100. This is equivalent to moving the decimal two places to the left.
- To convert a percent to a fraction, apply the definition of percent and then reduce.
- To convert a decimal or fraction to a percent, multiply by 1 in the form of 100%. This is equivalent to moving the decimal two places to the right and adding a percent sign.
- Pie charts are circular graphs where each sector is proportional to the size of the part out of the whole. The sum of the percentages must total 100%.
Topic Exercises
Part A: Decimals
Write as a mixed number.
1. 45.8
2. 15.4
3. 1.82
4. 2.55
5. 4.72
6. 3.14
Write as a decimal.
7.
8.
9.
10.
11.
12.
13.
14.
Perform the operations. Round dollar amounts to the nearest hundredth.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27. Find of $20.00.
28. Find of $33.26.
29. Find of $15.25.
30. Find of $15.50.
31. A gymnast scores 8.8 on the vault, 9.3 on the uneven bars, 9.1 on the balance beam, and 9.8 on the floor exercise. What is her overall average?
32. To calculate a batting average, divide the player’s number of hits by the total number of at-bats and round off the result to three decimal places. If a player has 62 hits in 195 at-bats, then what is his batting average?
Part B: Percents to Decimals
Convert each percent to its decimal equivalent.
33. 43%
34. 25%
35. 33%
36. 100%
37. 150%
38. 215%
39.
40.
41.
42.
43.
44.
45. 1.75%
46.
47. 0%
48. 1%
49.
50.
51. Convert one-half of one percent to a decimal.
52. Convert three-quarter percent to a decimal.
53. What is 20% of zero?
54. What is 50% of one hundred?
55. What is 150% of 100?
56. What is 20% of $20.00?
57. What is 112% of $210?
58. What is of $1,200?
59. If the bill at a restaurant comes to $32.50, what is the amount of a 15% tip?
60. Calculate the total cost, including a 20% tip, of a meal totaling $37.50.
61. If an item costs $45.25, then what is the total after adding 8.25% for tax?
62. If an item costs $36.95, then what is the total after adding 9¼% tax?
63. A retail outlet is offering 15% off the original $29.99 price of branded sweaters. What is the price after the discount?
64. A solar technology distribution company expects a 12% increase in first quarter sales as a result of a recently implemented rebate program. If the first quarter sales last year totaled $350,000, then what are the sales projections for the first quarter of this year?
65. If a local mayor of a town with a population of 40,000 people enjoys a 72% favorable rating in the polls, then how many people view the mayor unfavorably?
66. If a person earning $3,200 per month spends 32% of his monthly income on housing, then how much does he spend on housing each month?
Part C: Decimals and Fractions to Percents
Convert the following decimals and fractions to percents.
67. 0.67
68. 0.98
69. 1.30
70. 2.25
71.
72.
73.
74.
75.
76.
77.
78.
79. 0.0023
80. 0.000005
81. 20
82. 100
Part D: Percents to Fractions
Use the definition of percent to convert to fractions.
83. 20%
84. 80%
85. 57%
86. 97%
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99. 0.7%
100. 0.05%
101. 1.2%
102. 12.5%
The course grade weighting for a traditional mathematics course with 1,200 total points is shown in the pie chart below. Use the chart to answer the following questions.
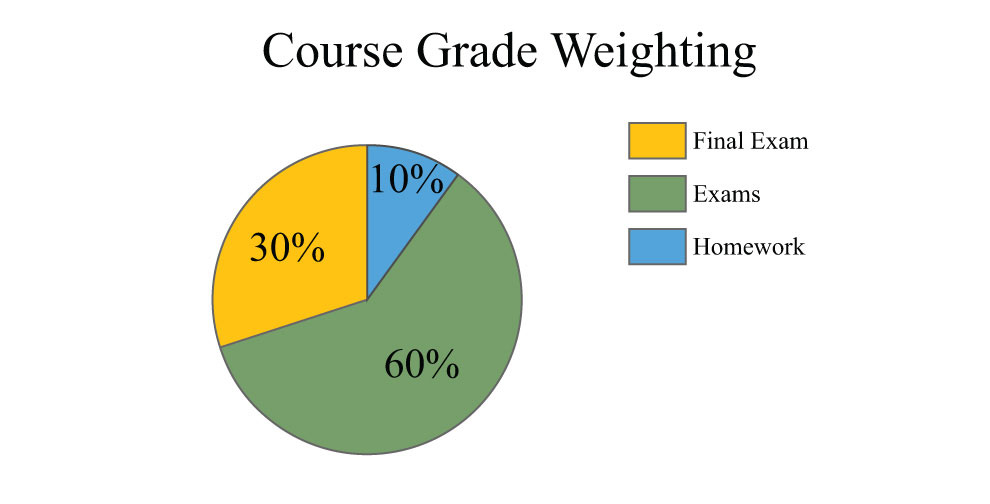
103. How many points will the final exam be worth?
104. How many points will the homework be worth?
105. How many points will each of the four regular exams be worth?
106. How many 10-point homework assignments can be assigned?
A website had 12,000 unique users in the fall of 2009. Answer the questions based on the pie chart below depicting total Web browser usage.
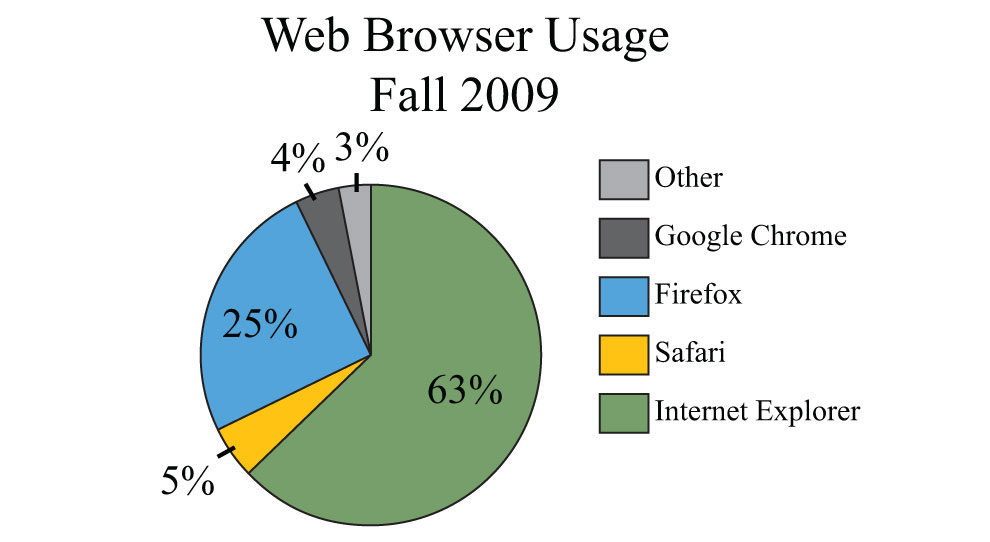
107. How many users used the Firefox Web browser?
108. How many users used a browser other than Internet Explorer?
109. How many users used either Firefox or Internet Explorer?
110. How many users used Google Chrome or Safari?
The 2009 employment status of 11.7 million full-time community college students is given in the following pie chart. Use the chart to answer the following questions. Round off each answer to the nearest hundredth.
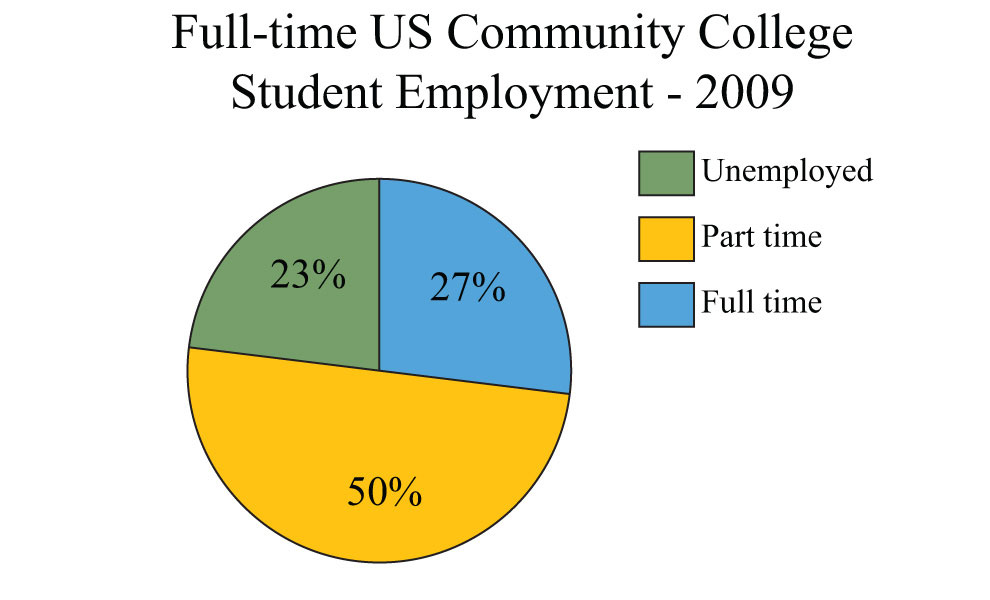
Source: American Association of Community Colleges.
111. How many full-time students were employed full time?
112. How many full-time students were employed part time?
113. How many full-time students were unemployed or employed part time?
114. How many full-time students also worked part time or full time?
The pie chart below depicts all US households categorized by income. The total number of households in 2007 was about 111,600,000. Use the chart to answer the following questions.
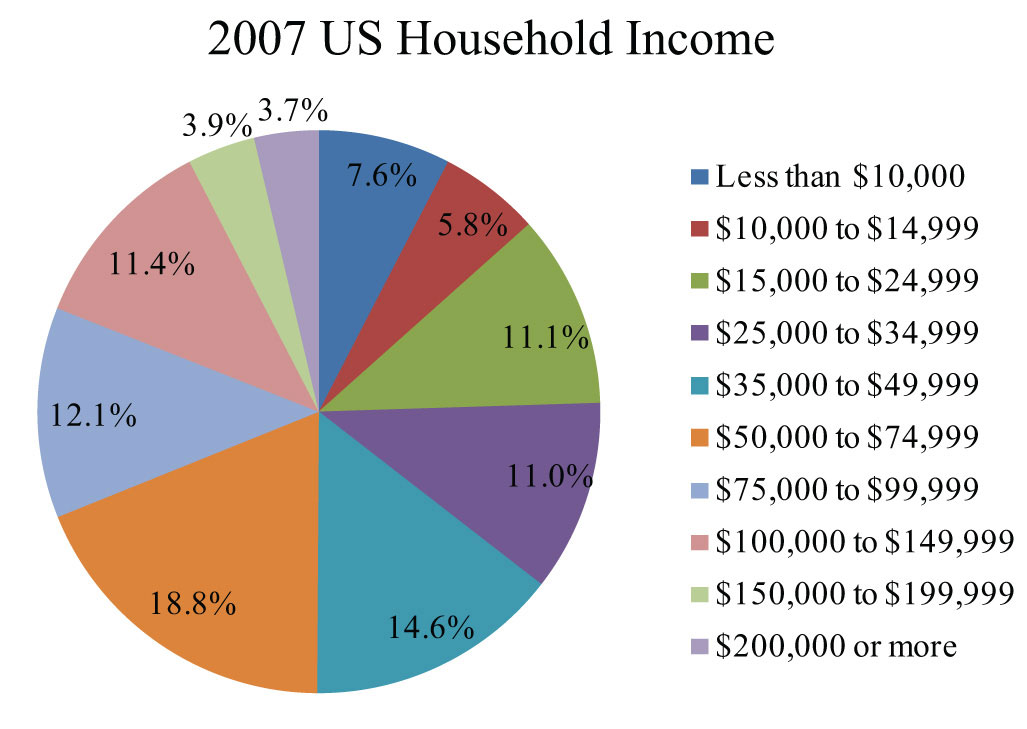
Source: US Census Bureau.
115. How many households reported an income from $50,000 to $74,999?
116. How many households reported an income from $75,000 to $99,999?
117. How many households reported an income of $100,000 or more?
118. How many households reported an income of less than $25,000?
Part E: Discussion Board Topics
119. The decimal system is considered a base-10 numeral system. Explain why. What other numeral systems are in use today?
120. Research and discuss the history of the symbol %.
121. Research and discuss simple interest and how it is calculated. Make up an example and share the solution.
122. Discuss methods for calculating tax and total bills.
123. Research and discuss the history of the pie chart.
124. Research and discuss the idea of a weighted average.
Answers
1:
3:
5:
7: 2.8
9: 3.125
11: 0.375
13:
15: 8.94
17: 53.451
19: 75.638
21: 0.6765
23: 7.23
25: 40.6
27: $3.33
29: $10.17
31: 9.25
33: 0.43
35: 0.33
37: 1.5
39: 0.005
41: 0.015
43: 0.00025
45: 0.0175
47: 0
49: 0.0305
51: 0.005
53: 0
55: 150
57: $235.20
59: $4.88
61: $48.98
63: $25.49
65: 11,200 people
67: 67%
69: 130%
71: 57%
73: 20%
75: 312.5%
77: 34%
79: 0.23%
81: 2,000%
83:
85:
87:
89:
91: 4
93: 1
95:
97:
99:
101:
103: 360 points
105: 180 points
107: 3,000 users
109: 10,560 users
111: 3.16 million
113: 8.54 million
115: 20,980,800 households
117: 21,204,000 households




