This is “Composition and Inverse Functions”, section 7.1 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
7.1 Composition and Inverse Functions
Learning Objectives
- Perform function composition.
- Determine whether or not given functions are inverses.
- Use the horizontal line test.
- Find the inverse of a one-to-one function algebraically.
Composition of Functions
In mathematics, it is often the case that the result of one function is evaluated by applying a second function. For example, consider the functions defined by and First, g is evaluated where and then the result is squared using the second function, f.

This sequential calculation results in 9. We can streamline this process by creating a new function defined by , which is explicitly obtained by substituting into
Therefore, and we can verify that when the result is 9.
The calculation above describes composition of functionsApplying a function to the results of another function., which is indicated using the composition operatorThe open dot used to indicate the function composition (). If given functions f and g,
The notation is read, “f composed with g.” This operation is only defined for values, x, in the domain of g such that is in the domain of f.

Example 1
Given and calculate:
Solution:
-
Substitute g into f.
-
Substitute f into g.
Answer:
The previous example shows that composition of functions is not necessarily commutative.
Example 2
Given and find
Solution:
Begin by finding
Next, substitute 4 in for x.
Answer:
Functions can be composed with themselves.
Example 3
Given find
Solution:
Answer:
Inverse Functions
Consider the function that converts degrees Fahrenheit to degrees Celsius: We can use this function to convert 77°F to degrees Celsius as follows.
Therefore, 77°F is equivalent to 25°C. If we wish to convert 25°C back to degrees Fahrenheit we would use the formula:
Notice that the two functions and each reverse the effect of the other.
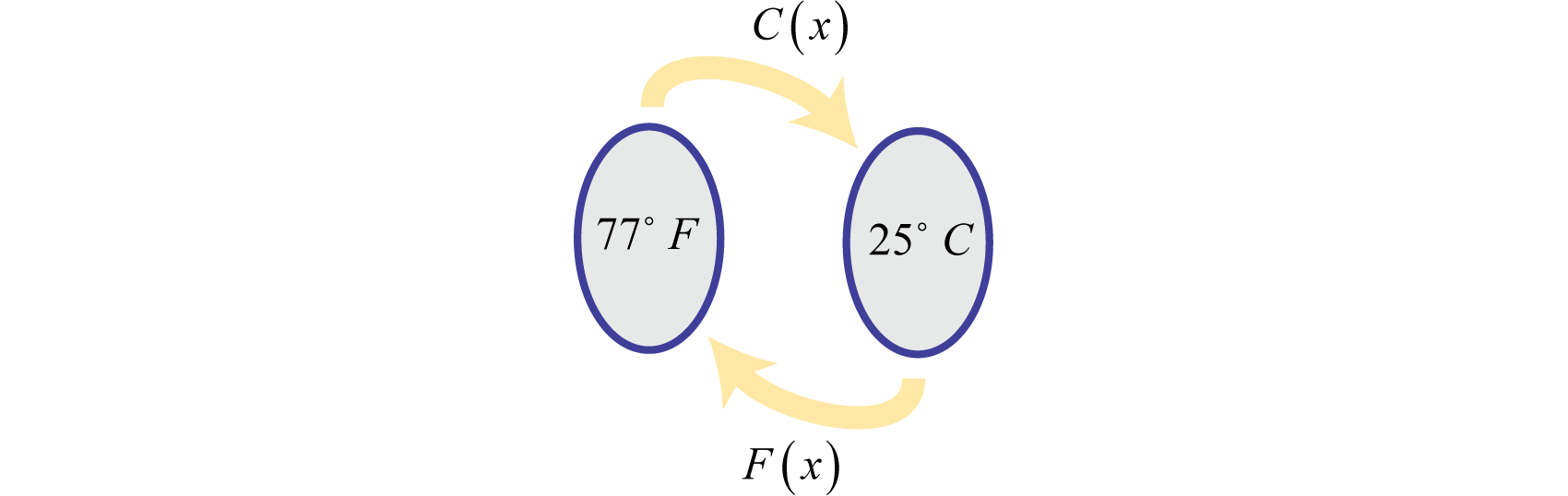
This describes an inverse relationship. In general, f and g are inverse functions if,
In this example,
Example 4
Verify algebraically that the functions defined by and are inverses.
Solution:
Compose the functions both ways and verify that the result is x.
Answer: Both ; therefore, they are inverses.
Next we explore the geometry associated with inverse functions. The graphs of both functions in the previous example are provided on the same set of axes below.
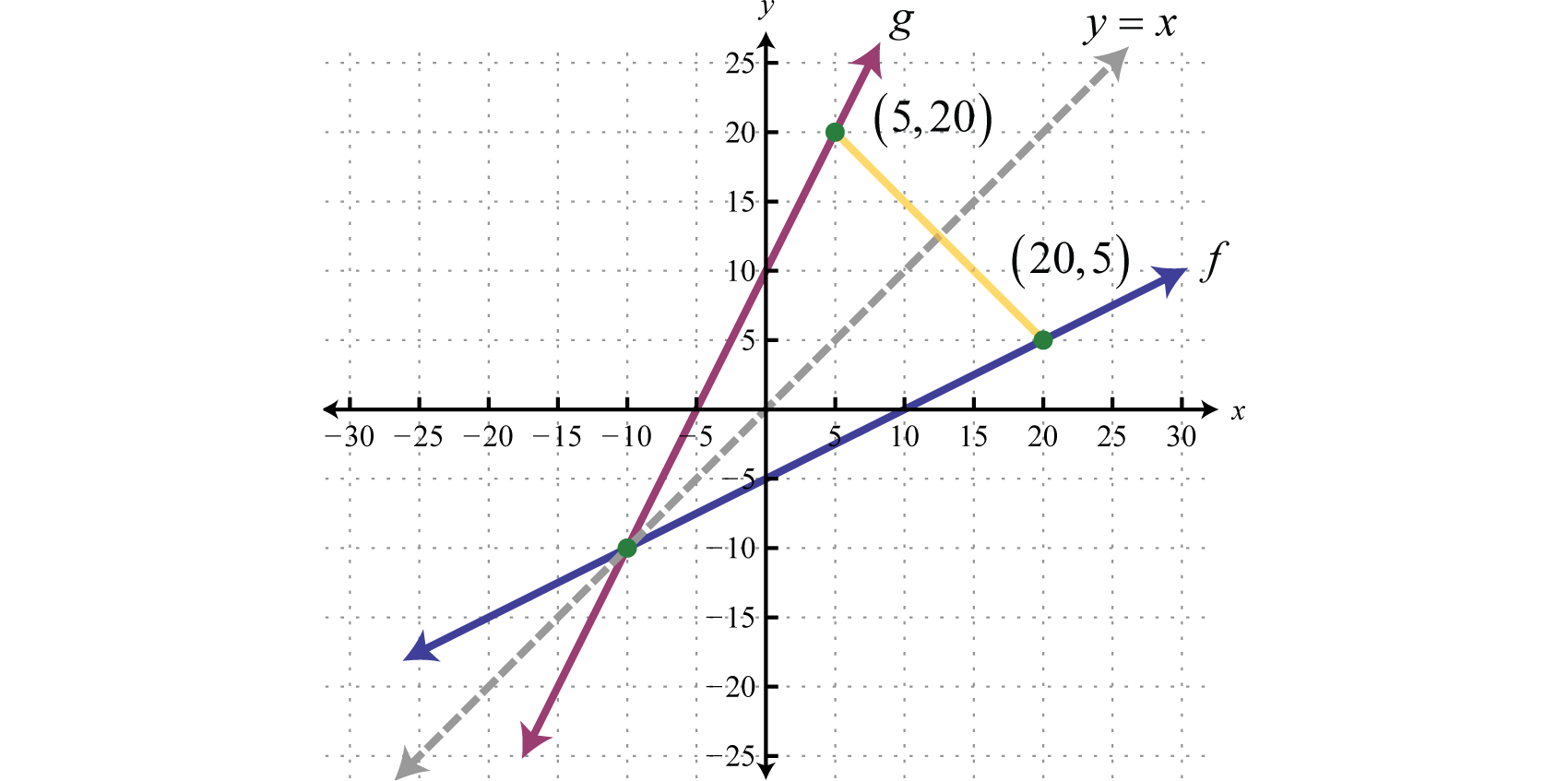
Note that there is symmetry about the line ; the graphs of f and g are mirror images about this line. Also notice that the point (20, 5) is on the graph of f and that (5, 20) is on the graph of g. Both of these observations are true in general and we have the following properties of inverse functions:
- The graphs of inverse functions are symmetric about the line
- If is on the graph of a function, then is on the graph of its inverse.
Furthermore, if g is the inverse of f we use the notation Here is read, “f inverse,” and should not be confused with negative exponents. In other words, and we have,
Example 5
Verify algebraically that the functions defined by and are inverses.
Solution:
Compose the functions both ways to verify that the result is x.
Answer: Since they are inverses.
Recall that a function is a relation where each element in the domain corresponds to exactly one element in the range. We use the vertical line test to determine if a graph represents a function or not. Functions can be further classified using an inverse relationship. One-to-one functionsFunctions where each value in the range corresponds to exactly one value in the domain. are functions where each value in the range corresponds to exactly one element in the domain. The horizontal line testIf a horizontal line intersects the graph of a function more than once, then it is not one-to-one. is used to determine whether or not a graph represents a one-to-one function. If a horizontal line intersects a graph more than once, then it does not represent a one-to-one function.
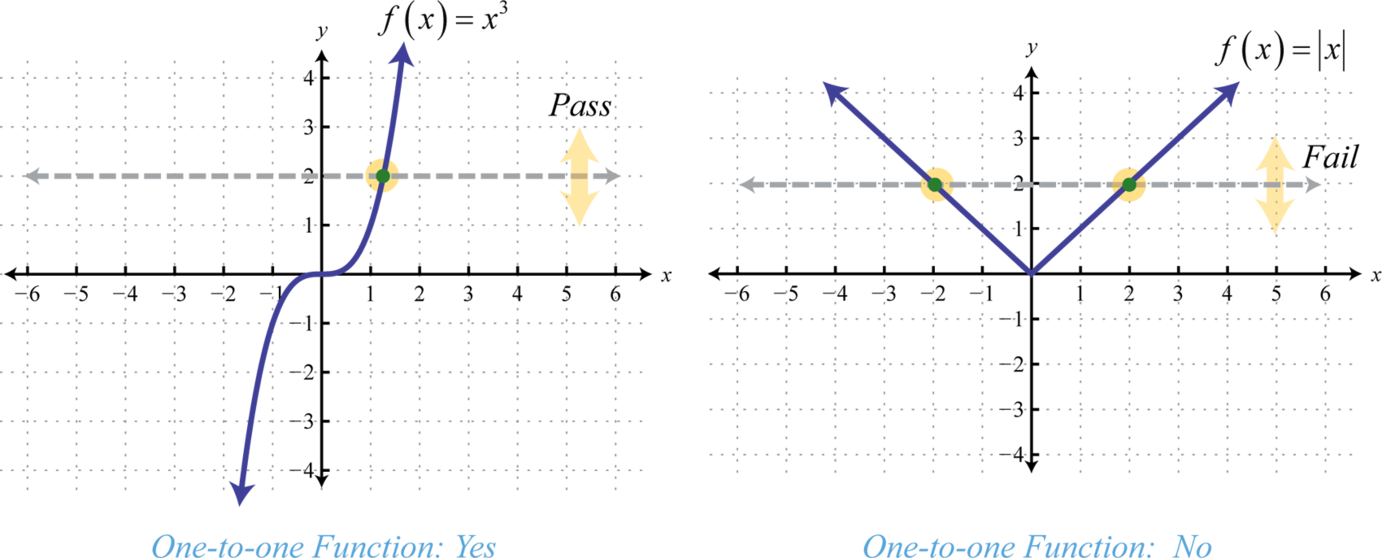
The horizontal line represents a value in the range and the number of intersections with the graph represents the number of values it corresponds to in the domain. The function defined by is one-to-one and the function defined by is not. Determining whether or not a function is one-to-one is important because a function has an inverse if and only if it is one-to-one. In other words, a function has an inverse if it passes the horizontal line test.
Note: In this text, when we say “a function has an inverse,” we mean that there is another function, , such that
Example 6
Determine whether or not the given function is one-to-one.

Solution:

Answer: The given function passes the horizontal line test and thus is one-to-one.
In fact, any linear function of the form where , is one-to-one and thus has an inverse. The steps for finding the inverse of a one-to-one function are outlined in the following example.
Example 7
Find the inverse of the function defined by
Solution:
Before beginning this process, you should verify that the function is one-to-one. In this case, we have a linear function where and thus it is one-to-one.
-
Step 1: Replace the function notation with y.
-
Step 2: Interchange x and y. We use the fact that if is a point on the graph of a function, then is a point on the graph of its inverse.
-
Step 3: Solve for y.
-
Step 4: The resulting function is the inverse of f. Replace y with
-
Step 5: Check.
Answer:
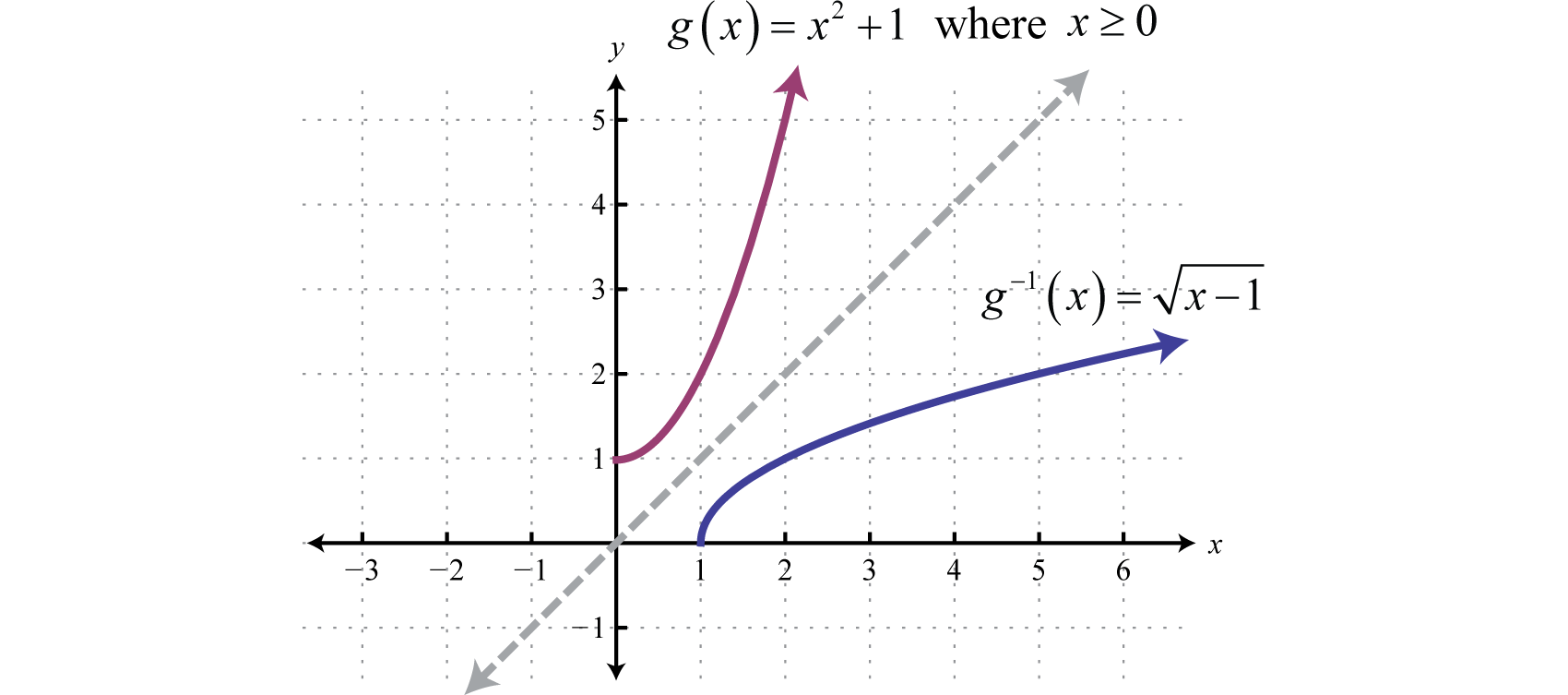
If a function is not one-to-one, it is often the case that we can restrict the domain in such a way that the resulting graph is one-to-one. For example, consider the squaring function shifted up one unit, Note that it does not pass the horizontal line test and thus is not one-to-one. However, if we restrict the domain to nonnegative values, , then the graph does pass the horizontal line test.
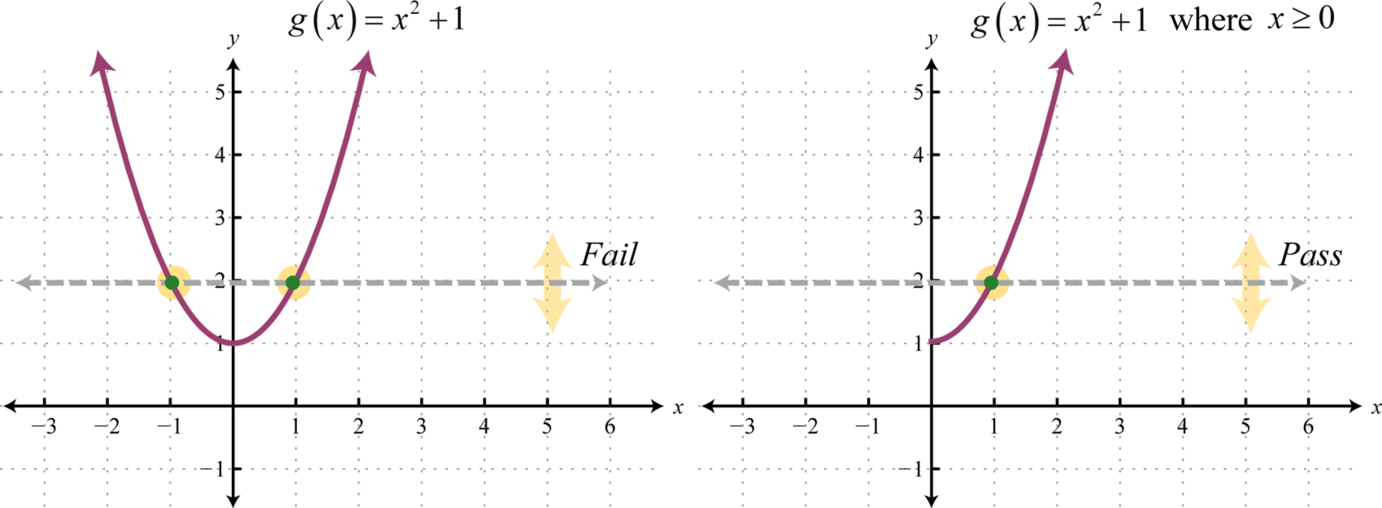
On the restricted domain, g is one-to-one and we can find its inverse.
Example 8
Find the inverse of the function defined by where
Solution:
Begin by replacing the function notation with y.
Interchange x and y.
Solve for y.
Since we only consider the positive result.
Answer: The check is left to the reader.
The graphs in the previous example are shown on the same set of axes below. Take note of the symmetry about the line
Example 9
Find the inverse of the function defined by
Solution:
Use a graphing utility to verify that this function is one-to-one. Begin by replacing the function notation with y.
Interchange x and y.
Solve for y.
Obtain all terms with the variable y on one side of the equation and everything else on the other. This will enable us to treat y as a GCF.
Answer: The check is left to the reader.
Key Takeaways
- The composition operator () indicates that we should substitute one function into another. In other words, indicates that we substitute into
- If two functions are inverses, then each will reverse the effect of the other. Using notation, and
- Inverse functions have special notation. If is the inverse of , then we can write This notation is often confused with negative exponents and does not equal one divided by
- The graphs of inverses are symmetric about the line If is a point on the graph of a function, then is a point on the graph of its inverse.
- If each point in the range of a function corresponds to exactly one value in the domain then the function is one-to-one. Use the horizontal line test to determine whether or not a function is one-to-one.
- A one-to-one function has an inverse, which can often be found by interchanging x and y, and solving for y. This new function is the inverse of the original function.
Topic Exercises
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Part A: Composition of Functions
Given the functions defined by f and g find and
Given the functions defined by , , and , calculate the following.
Given the functions defined by , , and , calculate the following.
Given the function, determine
-

-

-
-
-
-
-
-
-
-
-

-

-
-

-
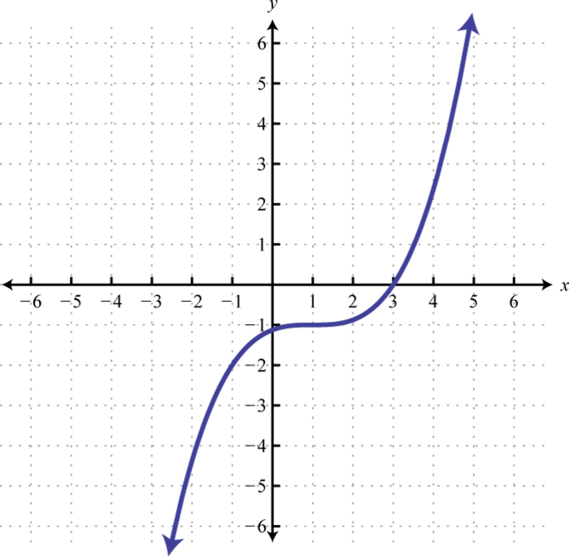
-
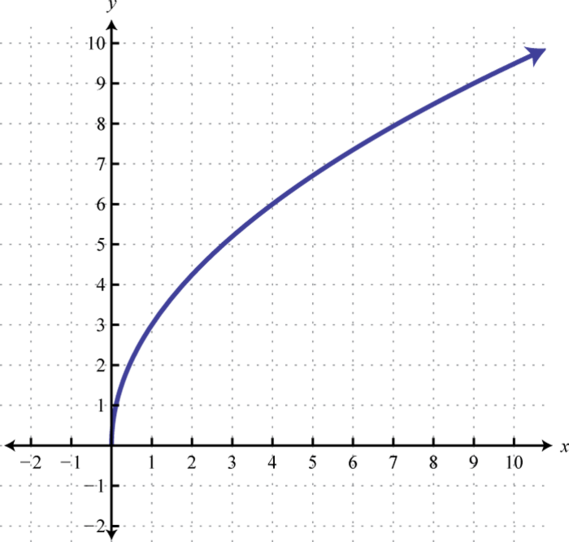
-
,
-
,
-
,
-
,
-
, ,
-
,
-
,
-
,
-
,
-
,
-
-
-
-
-
-
-
,
-
,
-
,
-
,
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
,
-
,
-
-
,
-
-
-
-
-
,
-
,
-
-
-
-
Part B: Inverse Functions
Are the given functions one-to-one? Explain.
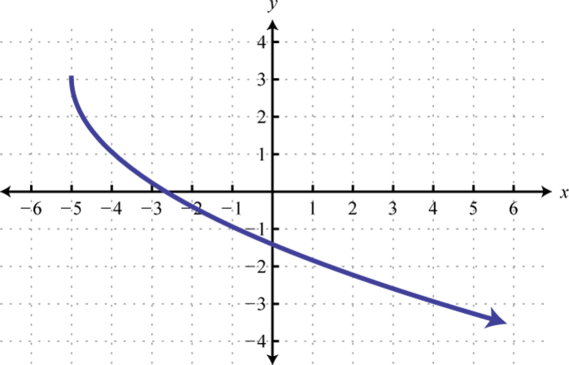
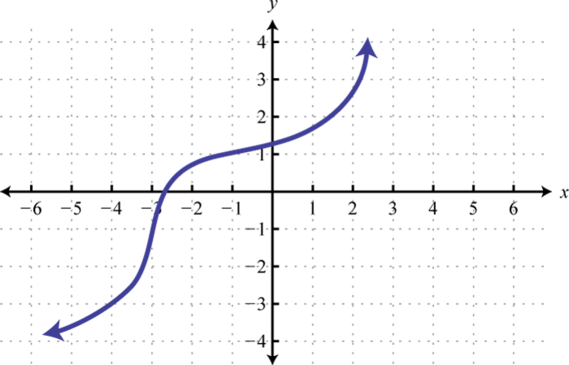
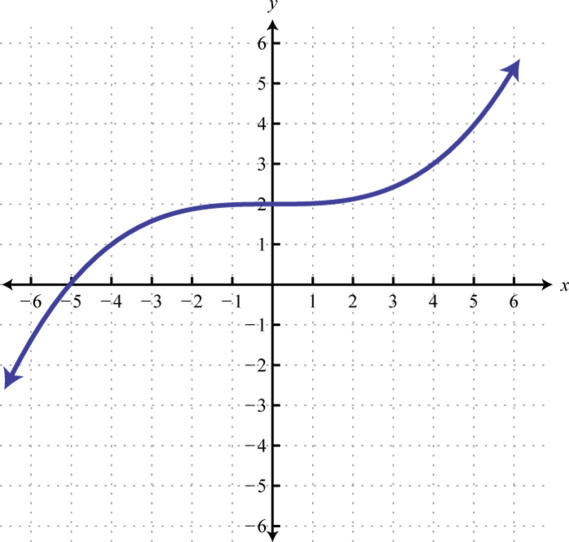
Given the graph of a one-to-one function, graph its inverse.
Verify algebraically that the two given functions are inverses. In other words, show that and
Find the inverses of the following functions.
Graph the function and its inverse on the same set of axes.
-
Is composition of functions associative? Explain.
-
Explain why and define inverse functions. Prove it algebraically.
-
Do the graphs of all straight lines represent one-to-one functions? Explain.
-
If the graphs of inverse functions intersect, then how can we find the point of intersection? Explain.
Part C: Discussion Board
Answers
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
-
-
;
-
-
361
-
-
−9
-
-
7
-
-
2
-
-
2
-
-
21
-
-
0
-
-
5
-
-
-
-
-
-
-
-
-
-
No, fails the HLT
-
-
Yes, passes the HLT
-
-
Yes, its graph passes the HLT.
-
-
No, its graph fails the HLT.
-
-
Yes, its graph passes the HLT.
-
-
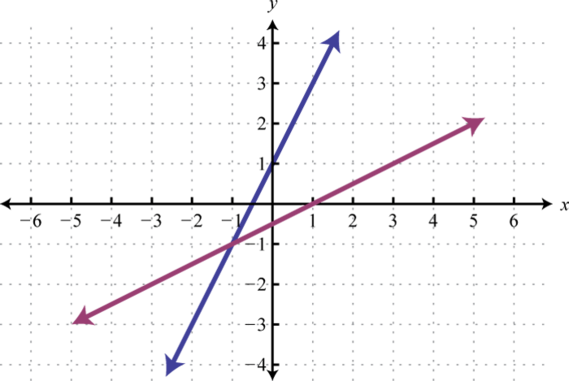
-
-

-
-
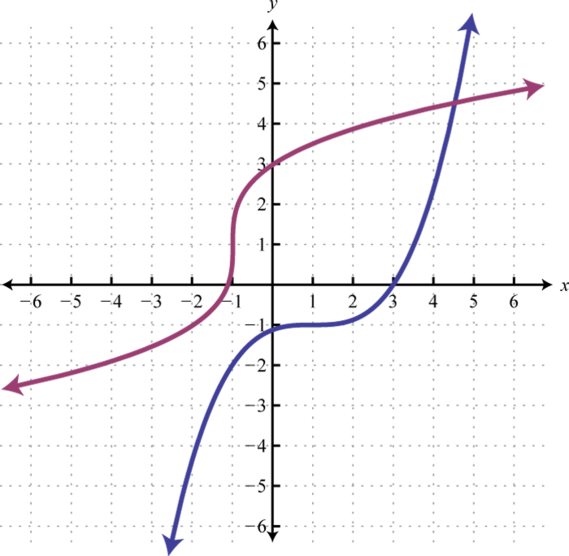
-
-
Proof
-
-
Proof
-
-
Proof
-
-
Proof
-
-
Proof
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-

-
-
-
-
-
-
-
-
-
-
Answer may vary
-
-
Answer may vary
-




