This is “Radical Functions and Equations”, chapter 5 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 5 Radical Functions and Equations
5.1 Roots and Radicals
Learning Objectives
- Identify and evaluate square and cube roots.
- Determine the domain of functions involving square and cube roots.
- Evaluate nth roots.
- Simplify radicals using the product and quotient rules for radicals.
Square and Cube Roots
Recall that a square rootA number that when multiplied by itself yields the original number. of a number is a number that when multiplied by itself yields the original number. For example, 5 is a square root of 25, because Since , we can say that −5 is a square root of 25 as well. Every positive real number has two square roots, one positive and one negative. For this reason, we use the radical sign to denote the principal (nonnegative) square rootThe positive square root of a positive real number, denoted with the symbol and a negative sign in front of the radical to denote the negative square root.
Zero is the only real number with one square root.
Example 1
Evaluate.
Solution:
If the radicandThe expression A within a radical sign, , the number inside the radical sign, can be factored as the square of another number, then the square root of the number is apparent. In this case, we have the following property:
Or more generally,
The absolute value is important because a may be a negative number and the radical sign denotes the principal square root. For example,
Make use of the absolute value to ensure a positive result.
Example 2
Simplify:
Solution:
Here the variable expression could be negative, zero, or positive. Since the sign depends on the unknown quantity x, we must ensure that we obtain the principal square root by making use of the absolute value.
Answer:
The importance of the use of the absolute value in the previous example is apparent when we evaluate using values that make the radicand negative. For example, when ,
Next, consider the square root of a negative number. To determine the square root of −25, you must find a number that when squared results in −25:
However, any real number squared always results in a positive number. The square root of a negative number is currently left undefined. For now, we will state that is not a real number. Therefore, the square root functionThe function defined by given by is not defined to be a real number if the x-values are negative. The smallest value in the domain is zero. For example, and Recall the graph of the square root function.
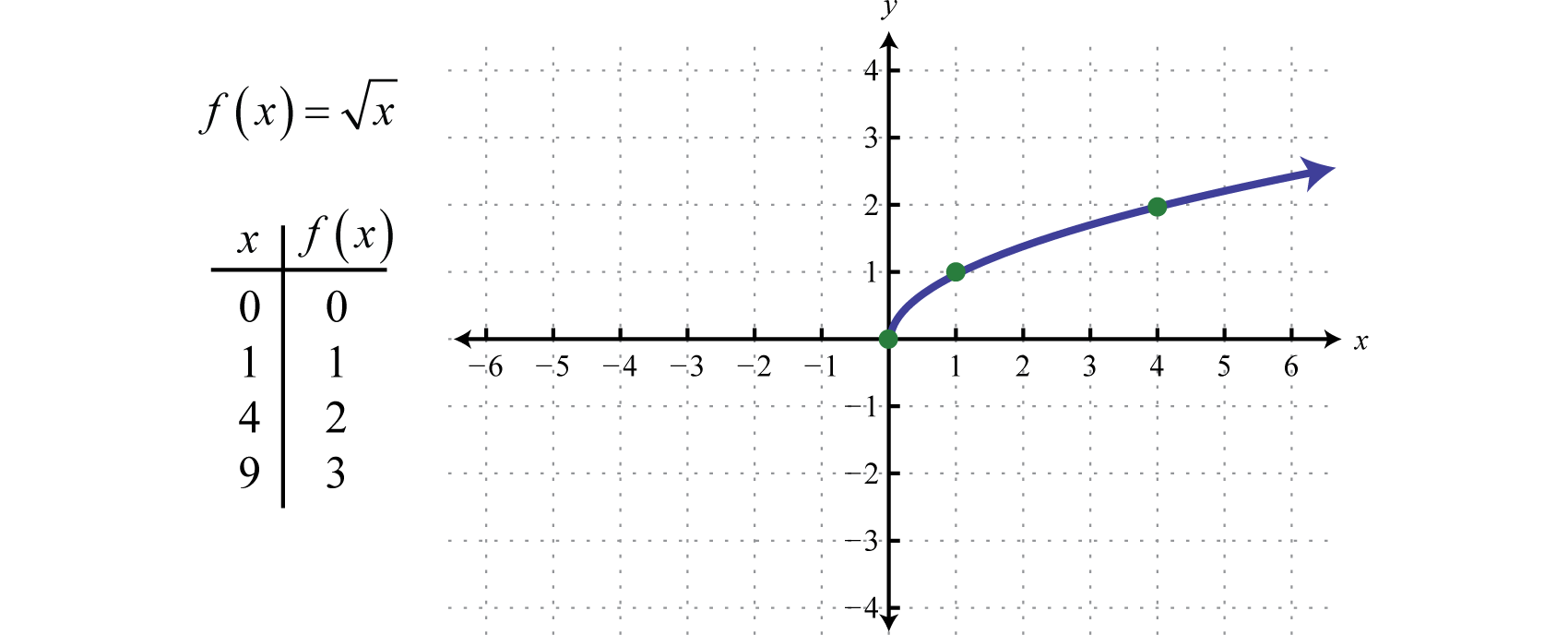
The domain and range both consist of real numbers greater than or equal to zero: To determine the domain of a function involving a square root we look at the radicand and find the values that produce nonnegative results.
Example 3
Determine the domain of the function defined by
Solution:
Here the radicand is This expression must be zero or positive. In other words,
Solve for x.
Answer: Domain:
A cube rootA number that when used as a factor with itself three times yields the original number, denoted with the symbol of a number is a number that when multiplied by itself three times yields the original number. Furthermore, we denote a cube root using the symbol , where 3 is called the indexThe positive integer n in the notation that is used to indicate an nth root.. For example,
The product of three equal factors will be positive if the factor is positive and negative if the factor is negative. For this reason, any real number will have only one real cube root. Hence the technicalities associated with the principal root do not apply. For example,
In general, given any real number a, we have the following property:
When simplifying cube roots, look for factors that are perfect cubes.
Example 4
Evaluate.
Solution:
It may be the case that the radicand is not a perfect square or cube. If an integer is not a perfect power of the index, then its root will be irrational. For example, is an irrational number that can be approximated on most calculators using the root button Depending on the calculator, we typically type in the index prior to pushing the button and then the radicand as follows:
Therefore, we have
Since cube roots can be negative, zero, or positive we do not make use of any absolute values.
Example 5
Simplify:
Solution:
The cube root of a quantity cubed is that quantity.
Answer:
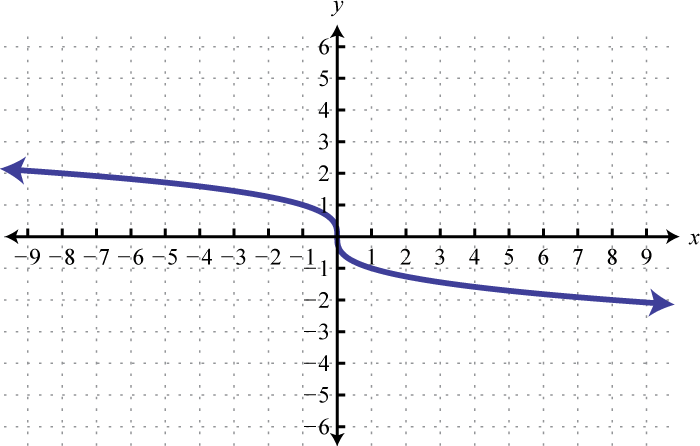
Next, consider the cube root functionThe function defined by :
Since the cube root could be either negative or positive, we conclude that the domain consists of all real numbers. Sketch the graph by plotting points. Choose some positive and negative values for x, as well as zero, and then calculate the corresponding y-values.
Plot the points and sketch the graph of the cube root function.
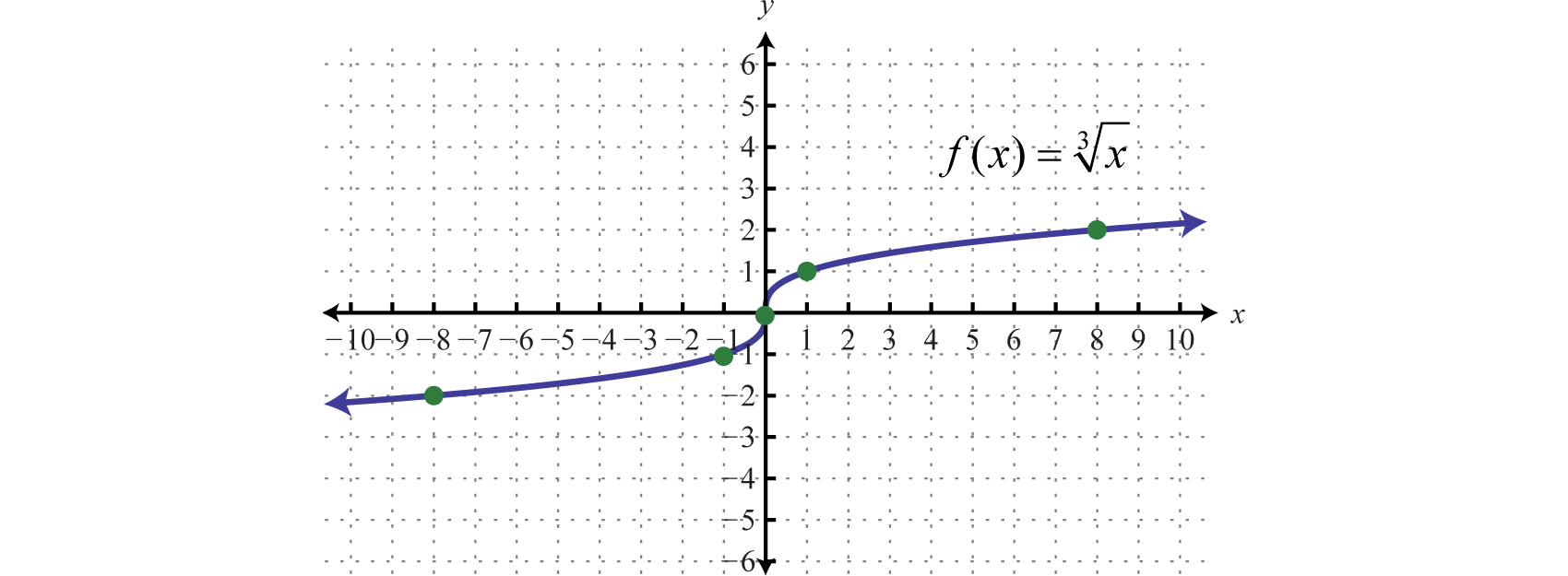
The graph passes the vertical line test and is indeed a function. In addition, the range consists of all real numbers.
Example 6
Given , find , , , and Sketch the graph of
Solution:
Replace x with the given values.
We can also sketch the graph using the following translations:
Answer:
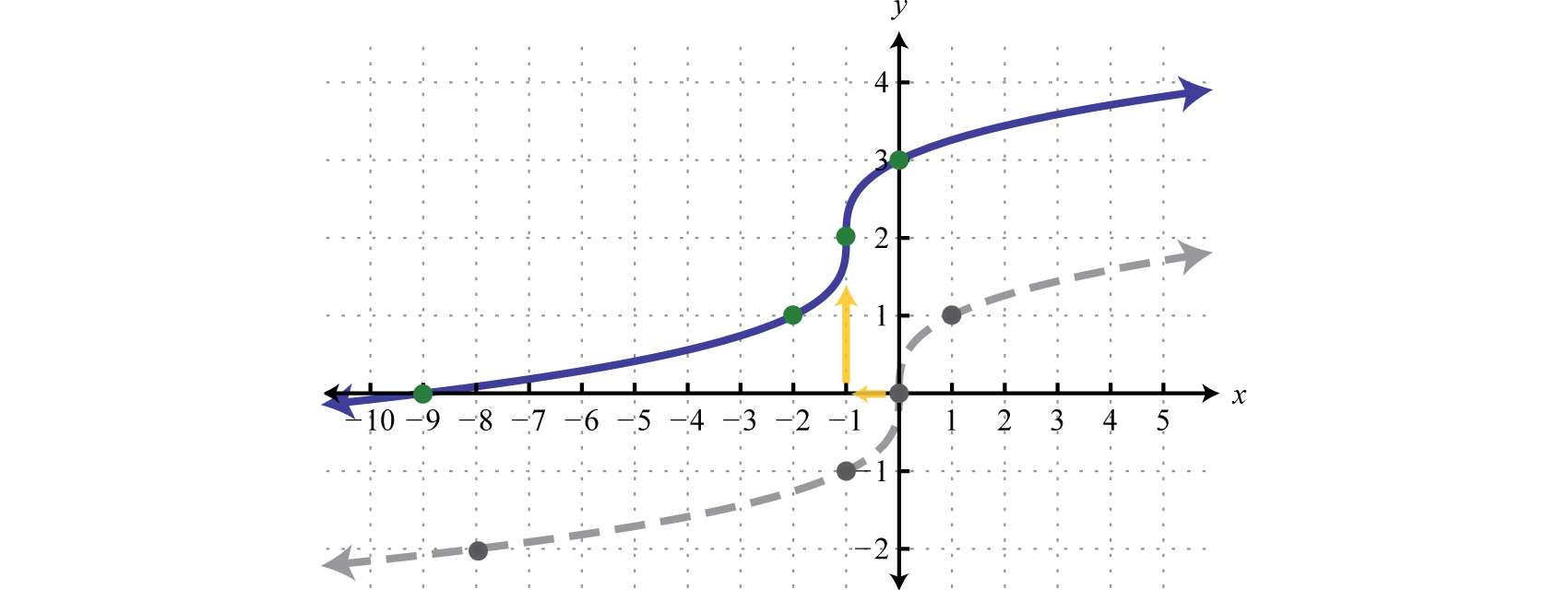
nth Roots
For any integer , we define an nth rootA number that when raised to the nth power yields the original number. of a positive real number as a number that when raised to the nth power yields the original number. Given any nonnegative real number a, we have the following property:
Here is called the index and is called the radicand. Furthermore, we can refer to the entire expression as a radicalUsed when referring to an expression of the form . When the index is an integer greater than or equal to 4, we say “fourth root,” “fifth root,” and so on. The nth root of any number is apparent if we can write the radicand with an exponent equal to the index.
Example 7
Simplify.
Solution:
Note: If the index is , then the radical indicates a square root and it is customary to write the radical without the index;
We have already taken care to define the principal square root of a real number. At this point, we extend this idea to nth roots when n is even. For example, 3 is a fourth root of 81, because And since , we can say that −3 is a fourth root of 81 as well. Hence we use the radical sign to denote the principal (nonnegative) nth rootThe positive nth root when n is even. when n is even. In this case, for any real number a, we use the following property:
For example,
The negative nth root, when n is even, will be denoted using a negative sign in front of the radical
We have seen that the square root of a negative number is not real because any real number that is squared will result in a positive number. In fact, a similar problem arises for any even index:
We can see that a fourth root of −81 is not a real number because the fourth power of any real number is always positive.
You are encouraged to try all of these on a calculator. What does it say?
Example 8
Simplify.
Solution:
Since the indices are even, use absolute values to ensure nonnegative results.
- is not a real number.
When the index n is odd, the same problems do not occur. The product of an odd number of positive factors is positive and the product of an odd number of negative factors is negative. Hence when the index n is odd, there is only one real nth root for any real number a. And we have the following property:
Example 9
Simplify.
Solution:
Since the indices are odd, the absolute value is not used.
In summary, for any real number a we have,
When n is odd, the nth root is positive or negative depending on the sign of the radicand.
When n is even, the nth root is positive or not real depending on the sign of the radicand.
Simplifying Radicals
It will not always be the case that the radicand is a perfect power of the given index. If it is not, then we use the product rule for radicalsGiven real numbers and , and the quotient rule for radicalsGiven real numbers and , where to simplify them. Given real numbers and ,
Product Rule for Radicals: |
|
Quotient Rule for Radicals: |
A radical is simplifiedA radical where the radicand does not consist of any factors that can be written as perfect powers of the index. if it does not contain any factors that can be written as perfect powers of the index.
Example 10
Simplify:
Solution:
Here 150 can be written as
We can verify our answer on a calculator:
Also, it is worth noting that
Answer:
Note: is the exact answer and 12.25 is an approximate answer. We present exact answers unless told otherwise.
Example 11
Simplify:
Solution:
Use the prime factorization of 160 to find the largest perfect cube factor:
Replace the radicand with this factorization and then apply the product rule for radicals.
We can verify our answer on a calculator.
Answer:
Example 12
Simplify:
Solution:
Here we note that the index is odd and the radicand is negative; hence the result will be negative. We can factor the radicand as follows:
Then simplify:
Answer:
Example 13
Simplify:
Solution:
In this case, consider the equivalent fraction with in the numerator and in the denominator and then simplify.
Answer:
Key Takeaways
- To simplify a square root, look for the largest perfect square factor of the radicand and then apply the product or quotient rule for radicals.
- To simplify a cube root, look for the largest perfect cube factor of the radicand and then apply the product or quotient rule for radicals.
- When working with nth roots, n determines the definition that applies. We use when n is odd and when n is even.
- To simplify nth roots, look for the factors that have a power that is equal to the index n and then apply the product or quotient rule for radicals. Typically, the process is streamlined if you work with the prime factorization of the radicand.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
-
-
-
-
-
-
-
-
-
-
-
Part A: Square and Cube Roots
Simplify.
Determine the domain of the given function.
Evaluate given the function definition.
Sketch the graph of the given function and give its domain and range.
Part B: nth Roots
Simplify.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Each side of a square has a length that is equal to the square root of the square’s area. If the area of a square is 72 square units, find the length of each of its sides.
-
Each edge of a cube has a length that is equal to the cube root of the cube’s volume. If the volume of a cube is 375 cubic units, find the length of each of its edges.
-
The current I measured in amperes is given by the formula where P is the power usage measured in watts and R is the resistance measured in ohms. If a 100 watt light bulb has 160 ohms of resistance, find the current needed. (Round to the nearest hundredth of an ampere.)
-
The time in seconds an object is in free fall is given by the formula where s represents the distance in feet the object has fallen. How long will it take an object to fall to the ground from the top of an 8-foot stepladder? (Round to the nearest tenth of a second.)
Part C: Simplifying Radicals
Simplify.
Simplify. Give the exact answer and the approximate answer rounded to the nearest hundredth.
Rewrite the following as a radical expression with coefficient 1.
-
Explain why there are two real square roots for any positive real number and one real cube root for any real number.
-
What is the square root of 1 and what is the cube root of 1? Explain why.
-
Explain why is not a real number and why is a real number.
-
Research and discuss the methods used for calculating square roots before the common use of electronic calculators.
Part D: Discussion Board
Answers
-
6
-
-
-
-
−4
-
-
5
-
-
Not a real number
-
-
−3
-
-
-
-
-
-
4
-
-
−6
-
-
−2
-
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
; ;
-
-
; ;
-
-
; ;
-
-
; ;
-
-
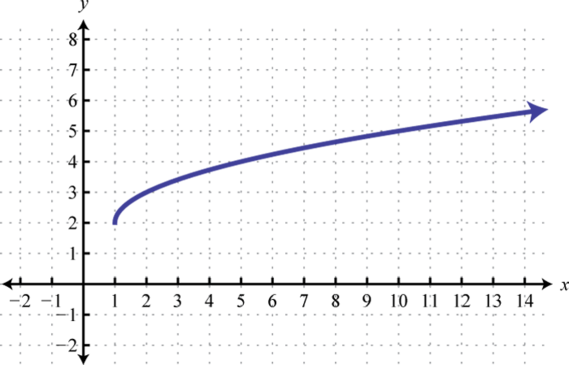
Domain: ; range:
-
-
Domain: ; range:
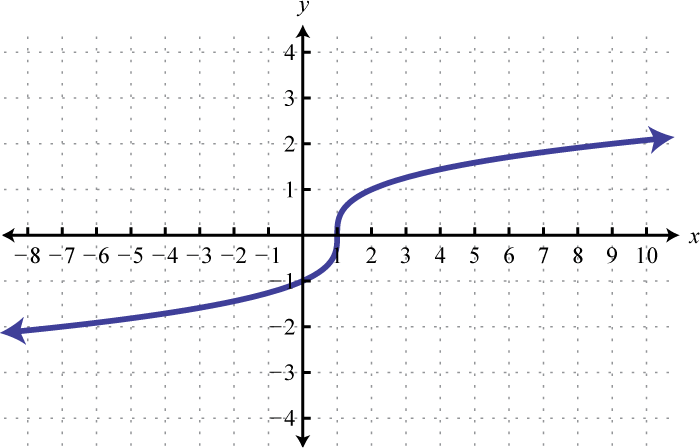
-
-
Domain: ; range:
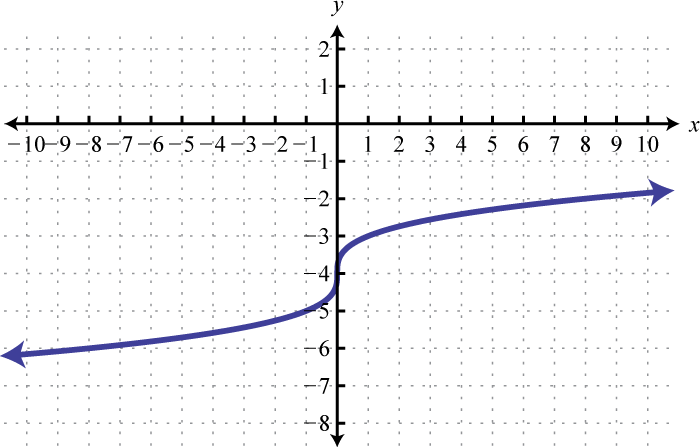
-
-
Domain: ; range:
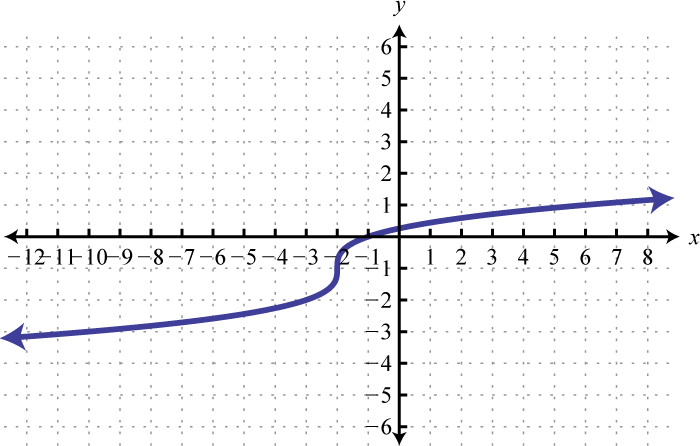
-
-
Domain: ; range:
-
-
Domain: ; range:
-
-
4
-
-
5
-
-
4
-
-
3
-
-
-
-
−2
-
-
−2
-
-
Not a real number
-
-
18
-
-
−20
-
-
Not a real number
-
-
-
-
3
-
-
-
-
20
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
; 7.75
-
-
; 1.40
-
-
; 6.21
-
-
; 1.32
-
-
; 4.70
-
-
-
-
-
-
-
-
-
-
units
-
-
Answer: 0.79 ampere
-
-
Answer may vary
-
-
Answer may vary
-
5.2 Simplifying Radical Expressions
Learning Objectives
- Simplify radical expressions using the product and quotient rule for radicals.
- Use formulas involving radicals.
Simplifying Radical Expressions
An algebraic expression that contains radicals is called a radical expressionAn algebraic expression that contains radicals.. We use the product and quotient rules to simplify them.
Example 1
Simplify:
Solution:
Use the fact that when n is odd.
Answer:
Example 2
Simplify:
Solution:
Use the fact that when n is even.
Since y is a variable, it may represent a negative number. Thus we need to ensure that the result is positive by including the absolute value.
Answer:
Important Note
Typically, at this point in algebra we note that all variables are assumed to be positive. If this is the case, then y in the previous example is positive and the absolute value operator is not needed. The example can be simplified as follows.
In this section, we will assume that all variables are positive. This allows us to focus on calculating nth roots without the technicalities associated with the principal nth root problem. For this reason, we will use the following property for the rest of the section,
When simplifying radical expressions, look for factors with powers that match the index.
Example 3
Simplify:
Solution:
Begin by determining the square factors of 12, , and
Make these substitutions, and then apply the product rule for radicals and simplify.
Answer:
Example 4
Simplify: .
Solution:
Begin by determining the square factors of 18, , and
Make these substitutions, apply the product and quotient rules for radicals, and then simplify.
Answer:
Example 5
Simplify:
Solution:
Begin by determining the cubic factors of 80, , and
Make these substitutions, and then apply the product rule for radicals and simplify.
Answer:
Example 6
Simplify .
Solution:
The coefficient , and thus does not have any perfect cube factors. It will be left as the only remaining radicand because all of the other factors are cubes, as illustrated below:
Replace the variables with these equivalents, apply the product and quotient rules for radicals, and then simplify.
Answer:
Example 7
Simplify:
Solution:
Determine all factors that can be written as perfect powers of 4. Here, it is important to see that Hence the factor will be left inside the radical.
Answer:
Example 8
Simplify:
Solution:
Notice that the variable factor x cannot be written as a power of 5 and thus will be left inside the radical. In addition, ; the factor y will be left inside the radical as well.
Answer:
Tip: To simplify finding an nth root, divide the powers by the index.
If the index does not divide into the power evenly, then we can use the quotient and remainder to simplify. For example,
The quotient is the exponent of the factor outside of the radical, and the remainder is the exponent of the factor left inside the radical.
Formulas Involving Radicals
Formulas often consist of radical expressions. For example, the period of a pendulum, or the time it takes a pendulum to swing from one side to the other and back, depends on its length according to the following formula.
Here T represents the period in seconds and L represents the length in feet of the pendulum.
Example 9
If the length of a pendulum measures feet, then calculate the period rounded to the nearest tenth of a second.
Solution:
Substitute for L and then simplify.
Answer: The period is approximately 1.36 seconds.
Frequently you need to calculate the distance between two points in a plane. To do this, form a right triangle using the two points as vertices of the triangle and then apply the Pythagorean theorem. Recall that the Pythagorean theorem states that if given any right triangle with legs measuring a and b units, then the square of the measure of the hypotenuse c is equal to the sum of the squares of the legs: In other words, the hypotenuse of any right triangle is equal to the square root of the sum of the squares of its legs.

Example 10
Find the distance between (−5, 3) and (1, 1).
Solution:
Form a right triangle by drawing horizontal and vertical lines though the two points. This creates a right triangle as shown below:
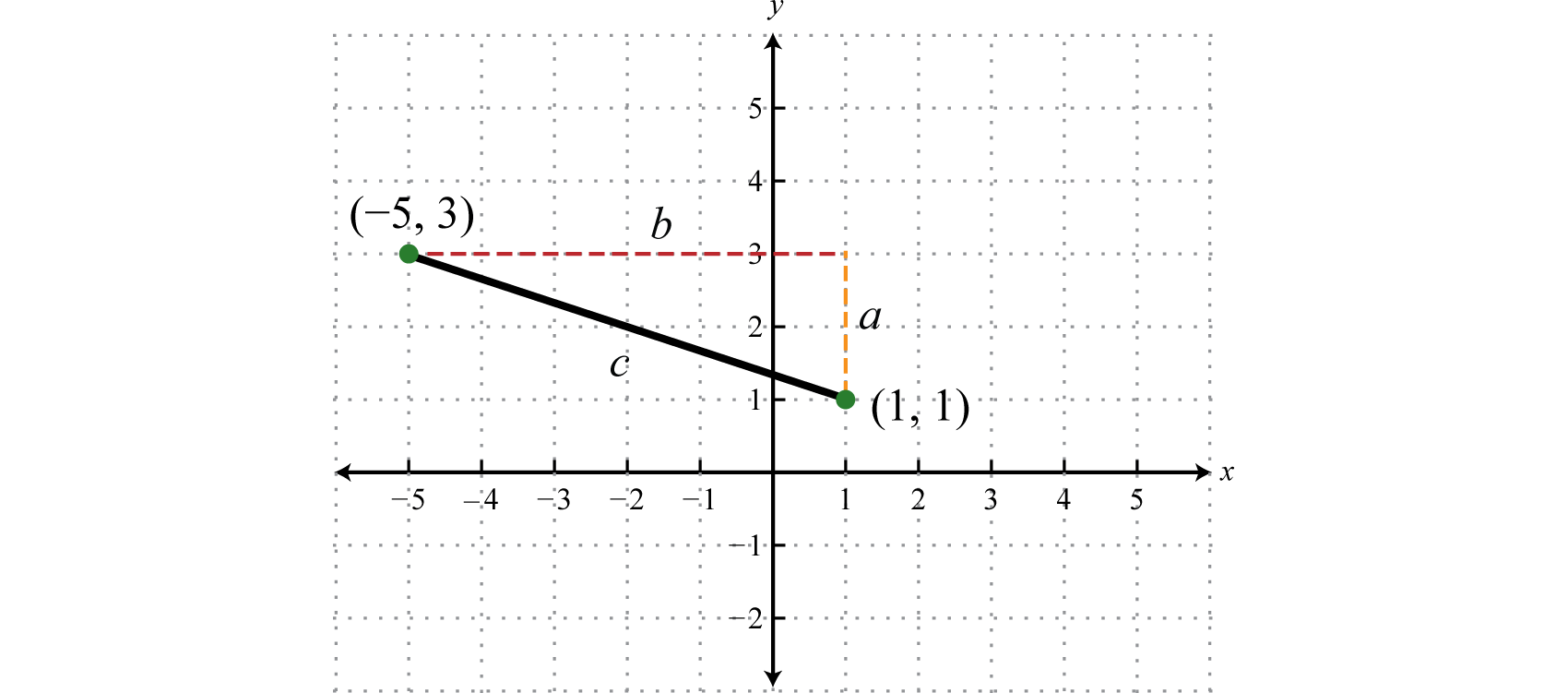
The length of leg b is calculated by finding the distance between the x-values of the given points, and the length of leg a is calculated by finding the distance between the given y-values.
Next, use the Pythagorean theorem to find the length of the hypotenuse.
Answer: The distance between the two points is units.
Generalize this process to produce a formula that can be used to algebraically calculate the distance between any two given points.

Given two points, and , the distance, d, between them is given by the distance formulaGiven two points and , calculate the distance d between them using the formula ,
Example 11
Calculate the distance between (−4, 7) and (2, 1).
Solution:
Use the distance formula with the following points.
It is a good practice to include the formula in its general form before substituting values for the variables; this improves readability and reduces the probability of making errors.
Answer: The distance between the two points is units.
Example 12
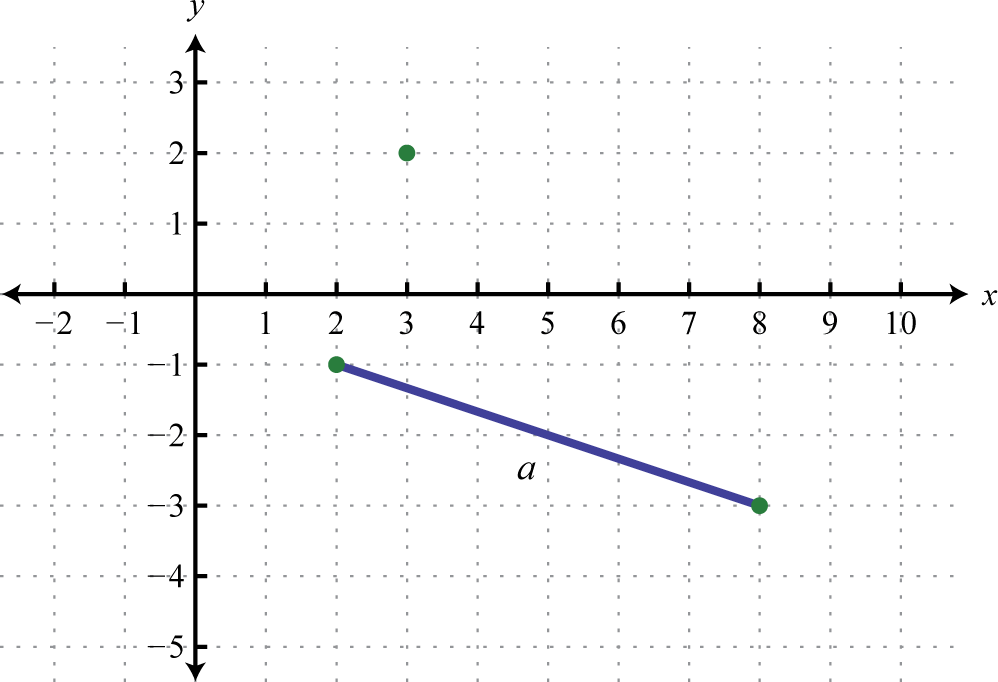
Do the three points (2, −1), (3, 2), and (8, −3) form a right triangle?
Solution:
The Pythagorean theorem states that having side lengths that satisfy the property is a necessary and sufficient condition of right triangles. In other words, if you can show that the sum of the squares of the leg lengths of the triangle is equal to the square of the length of the hypotenuse, then the triangle must be a right triangle. First, calculate the length of each side using the distance formula.
Geometry |
Calculation |
|---|---|
|
|
Points: (2, −1) and (8, −3)
|
|
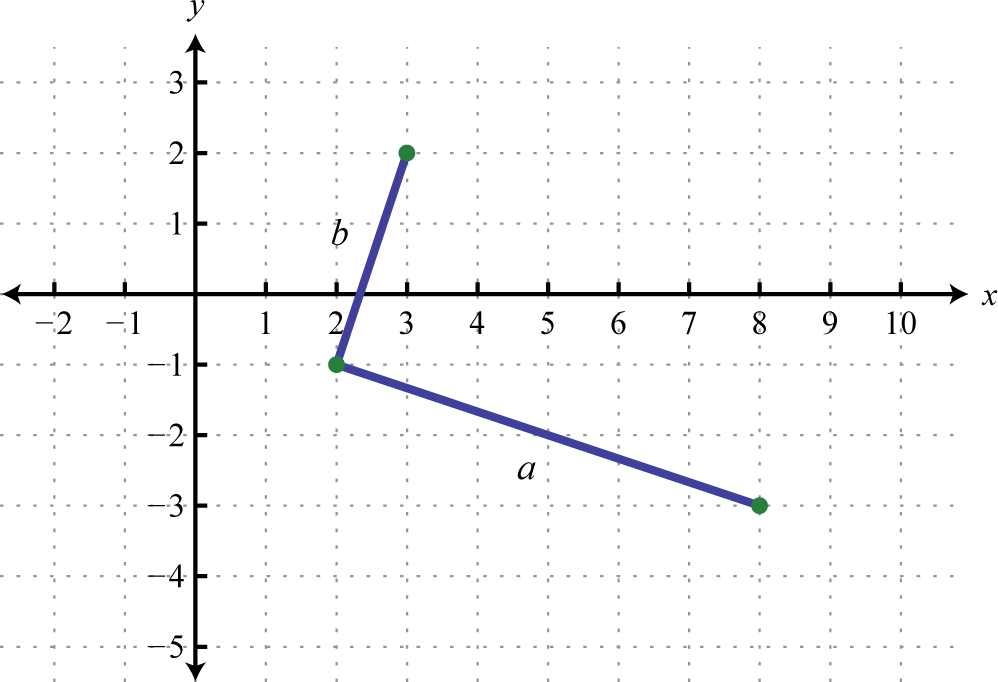
|
Points: (2, −1) and (3, 2)
|
|
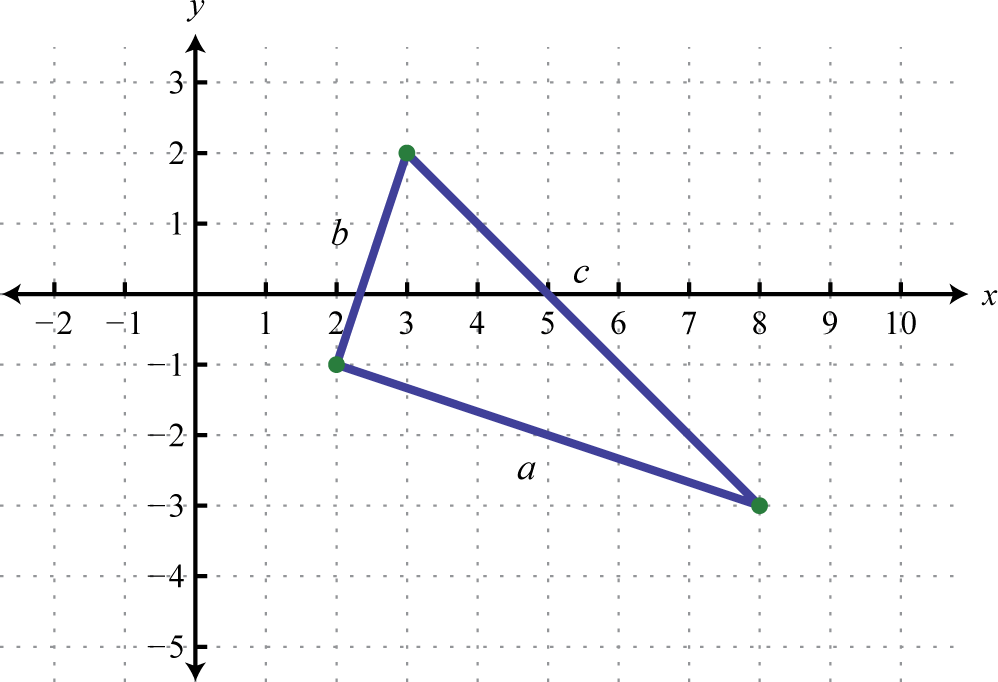
|
Points: (3, 2) and (8, −3)
|
Now we check to see if
Answer: Yes, the three points form a right triangle.
Try this! The speed of a vehicle before the brakes were applied can be estimated by the length of the skid marks left on the road. On wet concrete, the speed v in miles per hour can be estimated by the formula , where d represents the length of the skid marks in feet. Estimate the speed of a vehicle before applying the brakes if the skid marks left behind measure 27 feet. Round to the nearest mile per hour.
Answer: 18 miles per hour
Key Takeaways
- To simplify a radical expression, look for factors of the radicand with powers that match the index. If found, they can be simplified by applying the product and quotient rules for radicals, as well as the property , where a is nonnegative.
- A radical expression is simplified if its radicand does not contain any factors that can be written as perfect powers of the index.
- We typically assume that all variable expressions within the radical are nonnegative. This allows us to focus on simplifying radicals without the technical issues associated with the principal nth root. If this assumption is not made, we will ensure a positive result by using absolute values when simplifying radicals with even indices.
Topic Exercises
Part A: Simplifying Radical Expressions
Assume that the variable could represent any real number and then simplify.
Simplify. (Assume all variable expressions represent positive numbers.)
Rewrite the following as a radical expression with coefficient 1.
-
8 feet
-
32 feet
-
foot
-
foot
-
48 feet
-
80 feet
-
192 feet
-
288 feet
-
The speed of a vehicle before the brakes were applied can be estimated by the length of the skid marks left on the road. On dry pavement, the speed v in miles per hour can be estimated by the formula , where d represents the length of the skid marks in feet. Estimate the speed of a vehicle before applying the brakes on dry pavement if the skid marks left behind measure 27 feet. Round to the nearest mile per hour.
-
The radius r of a sphere can be calculated using the formula , where V represents the sphere’s volume. What is the radius of a sphere if the volume is cubic centimeters?
-
-
-
-
-
-
-
(5, −7) and (3, −8)
-
(−9, 7) and (−8, 4)
-
(−3, −4) and (3, −6)
-
(−5, −2) and (1, −6)
-
(−1, 1) and (−4, 10)
-
(8, −3) and (2, −12)
-
(0, −6) and (−3, 0)
-
(0, 0) and (8, −4)
-
and
-
and
-
(2,−1), (−1,2), and (6,3)
-
(−5,2), (−1, −2), and (−2,5)
-
(−5,0), (0,3), and (6,−1)
-
(−4,−1), (−2,5), and (7,2)
-
(1,−2), (2,3), and (−3,4)
-
(−2,1), (−1,−1), and (1,3)
-
(−4,0), (−2,−10), and (3,−9)
-
(0,0), (2,4), and (−2,6)
Part B: Formulas Involving Radicals
The period T in seconds of a pendulum is given by the formula where L represents the length in feet of the pendulum. Calculate the period, given each of the following lengths. Give the exact value and the approximate value rounded to the nearest tenth of a second.
The time t in seconds an object is in free fall is given by the formula where s represents the distance in feet the object has fallen. Calculate the time it takes an object to fall, given each of the following distances. Give the exact value and the approximate value rounded to the nearest tenth of a second.
Given the function find the y-intercept
Use the distance formula to calculate the distance between the given two points.
Determine whether or not the three points form a right triangle. Use the Pythagorean theorem to justify your answer.
-
Give a value for x such that Explain why it is important to assume that the variables represent nonnegative numbers.
-
Research and discuss the accomplishments of Christoph Rudolff. What is he credited for?
-
What is a surd, and where does the word come from?
-
Research ways in which police investigators can determine the speed of a vehicle after an accident has occurred. Share your findings on the discussion board.
Part D: Discussion Board
Answers
-
seconds; 3.1 seconds
-
-
seconds; 0.8 seconds
-
-
seconds; 1.7 seconds
-
-
seconds; 3.5 seconds
-
-
25 miles per hour
-
-
-
-
-
-
-
-
units
-
-
units
-
-
units
-
-
units
-
-
units
-
-
Right triangle
-
-
Not a right triangle
-
-
Right triangle
-
-
Right triangle
-
-
Answer may vary
-
-
Answer may vary
-
5.3 Adding and Subtracting Radical Expressions
Learning Objectives
- Add and subtract like radicals.
- Simplify radical expressions involving like radicals.
Adding and Subtracting Like Radicals
Adding and subtracting radical expressions is similar to adding and subtracting like terms. Radicals are considered to be like radicalsRadicals that share the same index and radicand., or similar radicalsTerm used when referring to like radicals., when they share the same index and radicand. For example, the terms and contain like radicals and can be added using the distributive property as follows:
Typically, we do not show the step involving the distributive property and simply write,
When adding terms with like radicals, add only the coefficients; the radical part remains the same.
Example 1
Add:
Solution:
The terms are like radicals; therefore, add the coefficients.
Answer:
Subtraction is performed in a similar manner.
Example 2
Subtract:
Solution:
Answer:
If the radicand and the index are not exactly the same, then the radicals are not similar and we cannot combine them.
Example 3
Simplify:
Solution:
We cannot simplify any further because and are not like radicals; the radicands are not the same.
Answer:
It is important to point out that We can verify this by calculating the value of each side with a calculator.
In general, note that
Example 4
Simplify:
Solution:
We cannot simplify any further, because and are not like radicals; the indices are not the same.
Answer:
Adding and Subtracting Radical Expressions
Often, we will have to simplify before we can identify the like radicals within the terms.
Example 5
Subtract:
Solution:
At first glance, the radicals do not appear to be similar. However, after simplifying completely, we will see that we can combine them.
Answer:
Example 6
Simplify:
Solution:
Begin by looking for perfect cube factors of each radicand.
Answer:
Next, we work with radical expressions involving variables. In this section, assume all radicands containing variable expressions are nonnegative.
Example 7
Simplify:
Solution:
Combine like radicals.
We cannot combine any further because the remaining radical expressions do not share the same radicand; they are not like radicals. Note:
Answer:
We will often find the need to subtract a radical expression with multiple terms. If this is the case, remember to apply the distributive property before combining like terms.
Example 8
Simplify:
Solution:
Answer:
Until we simplify, it is often unclear which terms involving radicals are similar. The general steps for simplifying radical expressions are outlined in the following example.
Example 9
Simplify:
Solution:
Step 1: Simplify the radical expression. In this case, distribute and then simplify each term that involves a radical.
Step2: Combine all like radicals. Remember to add only the coefficients; the variable parts remain the same.
Answer:
Example 10
Simplify:
Solution:
Answer:
Tip
Take careful note of the differences between products and sums within a radical. Assume both x and y are nonnegative.
The property says that we can simplify radicals when the operation in the radicand is multiplication. There is no corresponding property for addition.
Example 11
Calculate the perimeter of the triangle formed by the points , , and
Solution:
The formula for the perimeter of a triangle is where a, b, and c represent the lengths of each side. Plotting the points we have,
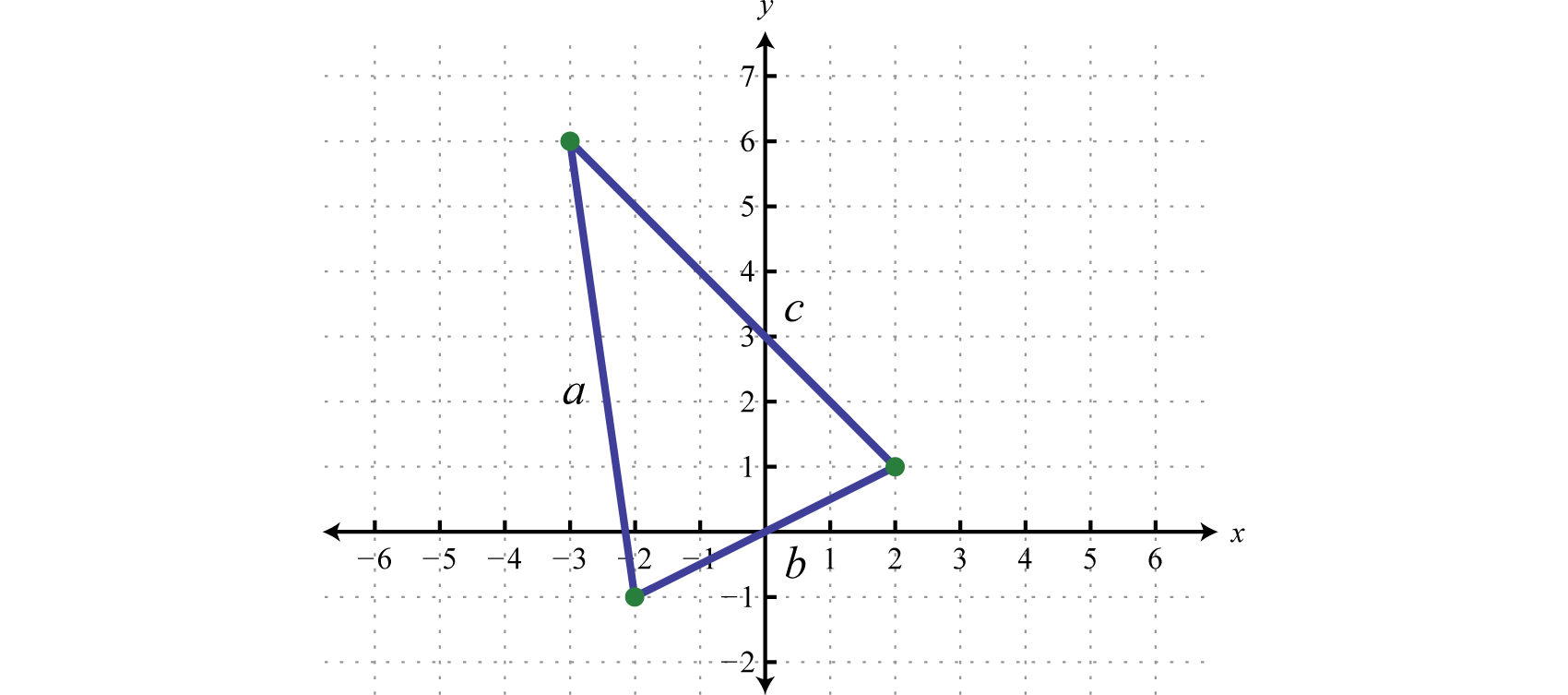
Use the distance formula to calculate the length of each side.
Similarly we can calculate the distance between (−3, 6) and (2,1) and find that units. Therefore, we can calculate the perimeter as follows:
Answer: units
Key Takeaways
- Add and subtract terms that contain like radicals just as you do like terms. If the index and radicand are exactly the same, then the radicals are similar and can be combined. This involves adding or subtracting only the coefficients; the radical part remains the same.
- Simplify each radical completely before combining like terms.
Topic Exercises
Part A: Adding and Subtracting Like Radicals
Simplify
Simplify. (Assume all radicands containing variable expressions are positive.)
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
{(−4, −5), (−4, 3), (2, 3)}
-
{(−1, 1), (3, 1), (3, −2)}
-
{(−3, 1), (−3, 5), (1, 5)}
-
{(−3, −1), (−3, 7), (1, −1)}
-
{(0,0), (2,4), (−2,6)}
-
{(−5,−2), (−3,0), (1,−6)}
-
A square garden that is 10 feet on each side is to be fenced in. In addition, the space is to be partitioned in half using a fence along its diagonal. How much fencing is needed to do this? (Round to the nearest tenth of a foot.)
-
A garden in the shape of a square has an area of 150 square feet. How much fencing is needed to fence it in? (Hint: The length of each side of a square is equal to the square root of the area. Round to the nearest tenth of a foot.)
Part B: Adding and Subtracting Radical Expressions
Simplify.
Simplify. (Assume all radicands containing variable expressions are positive.)
Calculate the perimeters of the triangles formed by the following sets of vertices.
-
Choose values for x and y and use a calculator to show that
-
Choose values for x and y and use a calculator to show that
Part C: Discussion Board
Answers
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
24 units
-
-
units
-
-
units
-
-
54.1 feet
-
-
Answer may vary
-
5.4 Multiplying and Dividing Radical Expressions
Learning Objectives
- Multiply radical expressions.
- Divide radical expressions.
- Rationalize the denominator.
Multiplying Radical Expressions
When multiplying radical expressions with the same index, we use the product rule for radicals. Given real numbers and ,
Example 1
Multiply:
Solution:
Apply the product rule for radicals, and then simplify.
Answer:
Often, there will be coefficients in front of the radicals.
Example 2
Multiply:
Solution:
Using the product rule for radicals and the fact that multiplication is commutative, we can multiply the coefficients and the radicands as follows.
Typically, the first step involving the application of the commutative property is not shown.
Answer:
Example 3
Multiply:
Solution:
Answer:
Use the distributive property when multiplying rational expressions with more than one term.
Example 4
Multiply: .
Solution:
Apply the distributive property and multiply each term by
Answer:
Example 5
Multiply:
Solution:
Apply the distributive property, and then simplify the result.
Answer:
The process for multiplying radical expressions with multiple terms is the same process used when multiplying polynomials. Apply the distributive property, simplify each radical, and then combine like terms.
Example 6
Multiply:
Solution:
Begin by applying the distributive property.

Answer:
The binomials and are called conjugatesThe factors and are conjugates.. When multiplying conjugate binomials the middle terms are opposites and their sum is zero.
Example 7
Multiply:
Solution:
Apply the distributive property, and then combine like terms.
Answer: 7
It is important to note that when multiplying conjugate radical expressions, we obtain a rational expression. This is true in general
Alternatively, using the formula for the difference of squares we have,
Dividing Radical Expressions
To divide radical expressions with the same index, we use the quotient rule for radicals. Given real numbers and ,
Example 8
Divide: .
Solution:
In this case, we can see that 6 and 96 have common factors. If we apply the quotient rule for radicals and write it as a single cube root, we will be able to reduce the fractional radicand.
Answer:
Example 9
Divide: .
Solution:
Write as a single square root and cancel common factors before simplifying.
Answer:
Rationalizing the Denominator
When the denominator (divisor) of a radical expression contains a radical, it is a common practice to find an equivalent expression where the denominator is a rational number. Finding such an equivalent expression is called rationalizing the denominatorThe process of determining an equivalent radical expression with a rational denominator..
To do this, multiply the fraction by a special form of 1 so that the radicand in the denominator can be written with a power that matches the index. After doing this, simplify and eliminate the radical in the denominator. For example:
Remember, to obtain an equivalent expression, you must multiply the numerator and denominator by the exact same nonzero factor.
Example 10
Rationalize the denominator:
Solution:
The goal is to find an equivalent expression without a radical in the denominator. The radicand in the denominator determines the factors that you need to use to rationalize it. In this example, multiply by 1 in the form
Answer:
Sometimes, we will find the need to reduce, or cancel, after rationalizing the denominator.
Example 11
Rationalize the denominator:
Solution:
In this example, we will multiply by 1 in the form
Notice that b does not cancel in this example. Do not cancel factors inside a radical with those that are outside.
Answer:
Up to this point, we have seen that multiplying a numerator and a denominator by a square root with the exact same radicand results in a rational denominator. In general, this is true only when the denominator contains a square root. However, this is not the case for a cube root. For example, Note that multiplying by the same factor in the denominator does not rationalize it. In this case, if we multiply by 1 in the form of , then we can write the radicand in the denominator as a power of 3. Simplifying the result then yields a rationalized denominator.
Therefore, to rationalize the denominator of a radical expression with one radical term in the denominator, begin by factoring the radicand of the denominator. The factors of this radicand and the index determine what we should multiply by. Multiply the numerator and denominator by the nth root of factors that produce nth powers of all the factors in the radicand of the denominator.
Example 12
Rationalize the denominator:
Solution:
The radical in the denominator is equivalent to To rationalize the denominator, we need: To obtain this, we need one more factor of 5. Therefore, multiply by 1 in the form of
Answer:
Example 13
Rationalize the denominator: .
Solution:
In this example, we will multiply by 1 in the form .
Answer:
Example 14
Rationalize the denominator: .
Solution:
In this example, we will multiply by 1 in the form .
Answer:
When two terms involving square roots appear in the denominator, we can rationalize it using a very special technique. This technique involves multiplying the numerator and the denominator of the fraction by the conjugate of the denominator. Recall that multiplying a radical expression by its conjugate produces a rational number.
Example 15
Rationalize the denominator:
Solution:
In this example, the conjugate of the denominator is Therefore, multiply by 1 in the form
Answer:
Notice that the terms involving the square root in the denominator are eliminated by multiplying by the conjugate. We can use the property to expedite the process of multiplying the expressions in the denominator.
Example 16
Rationalize the denominator: .
Solution:
Multiply by 1 in the form .
Answer:
Example 17
Rationalize the denominator: .
Solution:
In this example, we will multiply by 1 in the form
Answer:
Key Takeaways
- To multiply two single-term radical expressions, multiply the coefficients and multiply the radicands. If possible, simplify the result.
- Apply the distributive property when multiplying a radical expression with multiple terms. Then simplify and combine all like radicals.
- Multiplying a two-term radical expression involving square roots by its conjugate results in a rational expression.
- It is common practice to write radical expressions without radicals in the denominator. The process of finding such an equivalent expression is called rationalizing the denominator.
- If an expression has one term in the denominator involving a radical, then rationalize it by multiplying the numerator and denominator by the nth root of factors of the radicand so that their powers equal the index.
- If a radical expression has two terms in the denominator involving square roots, then rationalize it by multiplying the numerator and denominator by the conjugate of the denominator.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
What is the perimeter and area of a rectangle with length measuring centimeters and width measuring centimeters?
-
What is the perimeter and area of a rectangle with length measuring centimeters and width measuring centimeters?
-
If the base of a triangle measures meters and the height measures meters, then calculate the area.
-
If the base of a triangle measures meters and the height measures meters, then calculate the area.
Part A: Multiplying Radical Expressions
Multiply. (Assume all variables represent non-negative real numbers.)
Part B: Dividing Radical Expressions
Divide. (Assume all variables represent positive real numbers.)
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The radius of the base of a right circular cone is given by where V represents the volume of the cone and h represents its height. Find the radius of a right circular cone with volume 50 cubic centimeters and height 4 centimeters. Give the exact answer and the approximate answer rounded to the nearest hundredth.
-
The radius of a sphere is given by where V represents the volume of the sphere. Find the radius of a sphere with volume 135 square centimeters. Give the exact answer and the approximate answer rounded to the nearest hundredth.
Part C: Rationalizing the Denominator
Rationalize the denominator. (Assume all variables represent positive real numbers.)
-
Research and discuss some of the reasons why it is a common practice to rationalize the denominator.
-
Explain in your own words how to rationalize the denominator.
Part D: Discussion
Answers
-
-
-
-
-
-
-
7
-
-
-
-
20
-
-
-
-
-
-
-
-
3
-
-
-
-
-
-
-
-
16
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
10
-
-
-
-
Perimeter: centimeters; area: square centimeters
-
-
square meters
-
-
5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
centimeters; 3.45 centimeters
-
-
Answer may vary
-
5.5 Rational Exponents
Learning Objectives
- Write expressions with rational exponents in radical form.
- Write radical expressions with rational exponents.
- Perform operations and simplify expressions with rational exponents.
- Perform operations on radicals with different indices.
Rational Exponents
So far, exponents have been limited to integers. In this section, we will define what rational (or fractional) exponents mean and how to work with them. All of the rules for exponents developed up to this point apply. In particular, recall the product rule for exponents. Given any rational numbers m and n, we have For example, if we have an exponent of 1/2, then the product rule for exponents implies the following: Here is one of two equal factors of 5; hence it is a square root of 5, and we can write Furthermore, we can see that is one of three equal factors of 2. Therefore, is a cube root of 2, and we can write This is true in general, given any nonzero real number a and integer , In other words, the denominator of a fractional exponent determines the index of an nth root.
Example 1
Rewrite as a radical.
Solution:
Example 2
Rewrite as a radical and then simplify.
Solution:
Example 3
Rewrite as a radical and then simplify.
Solution:
a.
b.
Next, consider fractional exponents where the numerator is an integer other than 1. For example, consider the following:
This shows that is one of three equal factors of In other words, is a cube root of and we can write:
In general, given any nonzero real number a where m and n are positive integers (),
An expression with a rational exponentThe fractional exponent m/n that indicates a radical with index n and exponent m: is equivalent to a radical where the denominator is the index and the numerator is the exponent. Any radical expression can be written with a rational exponent, which we call exponential formAn equivalent expression written using a rational exponent..
Example 4
Rewrite as a radical.
Solution:
Example 5
Rewrite as a radical and then simplify.
Solution:
We can often avoid very large integers by working with their prime factorization.
a.
b.
Given a radical expression, we might want to find the equivalent in exponential form. Assume all variables are positive.
Example 6
Rewrite using rational exponents:
Solution:
Here the index is 5 and the power is 3. We can write
Answer:
Example 7
Rewrite using rational exponents:
Solution:
Here the index is 6 and the power is 3. We can write
Answer:
It is important to note that the following are equivalent.
In other words, it does not matter if we apply the power first or the root first. For example, we can apply the power before the nth root:
Or we can apply the nth root before the power:
The results are the same.
Example 8
Rewrite as a radical and then simplify:
Solution:
Here the index is 3 and the power is 2. We can write
Answer: 4
Some calculators have a caret button which is used for entering exponents. If so, we can calculate approximations for radicals using it and rational exponents. For example, to calculate , we make use of the parenthesis buttons and type
To calculate , we would type
Operations Using the Rules of Exponents
In this section, we review all of the rules of exponents, which extend to include rational exponents. If given any rational numbers m and n, then we have
Product rule for exponents: |
|
Quotient rule for exponents: |
|
Power rule for exponents: |
|
Power rule for a product: |
|
Power rule for a quotient: |
|
Negative exponents: |
|
Zero exponent: |
These rules allow us to perform operations with rational exponents.
Example 9
Simplify:
Solution:
Answer:
Example 10
Simplify: .
Solution:
Answer:
Example 11
Simplify:
Solution:
Answer:
Example 12
Simplify: .
Solution:
Answer:
Example 13
Simplify:
Solution:
Answer:
Radical Expressions with Different Indices
To apply the product or quotient rule for radicals, the indices of the radicals involved must be the same. If the indices are different, then first rewrite the radicals in exponential form and then apply the rules for exponents.
Example 14
Multiply:
Solution:
In this example, the index of each radical factor is different. Hence the product rule for radicals does not apply. Begin by converting the radicals into an equivalent form using rational exponents. Then apply the product rule for exponents.
Answer:
Example 15
Divide: .
Solution:
In this example, the index of the radical in the numerator is different from the index of the radical in the denominator. Hence the quotient rule for radicals does not apply. Begin by converting the radicals into an equivalent form using rational exponents and then apply the quotient rule for exponents.
Answer:
Example 16
Simplify:
Solution:
Here the radicand of the square root is a cube root. After rewriting this expression using rational exponents, we will see that the power rule for exponents applies.
Answer:
Key Takeaways
- Any radical expression can be written in exponential form:
- Fractional exponents indicate radicals. Use the numerator as the power and the denominator as the index of the radical.
- All the rules of exponents apply to expressions with rational exponents.
- If operations are to be applied to radicals with different indices, first rewrite the radicals in exponential form and then apply the rules for exponents.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Explain why (−4)^(3/2) gives an error on a calculator and −4^(3/2) gives an answer of −8.
-
Marcy received a text message from Mark asking her age. In response, Marcy texted back “125^(2/3) years old.” Help Mark determine Marcy’s age.
Part A: Rational Exponents
Express using rational exponents.
Express in radical form.
Write as a radical and then simplify.
Use a calculator to approximate an answer rounded to the nearest hundredth.
Part B: Operations Using the Rules of Exponents
Perform the operations and simplify. Leave answers in exponential form.
Part C: Radical Expressions with Different Indices
Perform the operations.
-
Who is credited for devising the notation that allows for rational exponents? What are some of his other accomplishments?
-
When using text, it is best to communicate nth roots using rational exponents. Give an example.
Part D: Discussion Board
Answers
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
2
-
-
2
-
-
-
-
−3
-
-
2
-
-
-
-
10
-
-
-
-
27
-
-
32
-
-
64
-
-
-
-
9
-
-
−8
-
-
1.41
-
-
1.68
-
-
1.38
-
-
Not a real number
-
-
Answer may vary
-
-
25
-
-
-
-
-
-
125
-
-
-
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Answer may vary
-
5.6 Solving Radical Equations
Learning Objectives
- Solve equations involving square roots.
- Solve equations involving cube roots.
Radical Equations
A radical equationAny equation that contains one or more radicals with a variable in the radicand. is any equation that contains one or more radicals with a variable in the radicand. Following are some examples of radical equations, all of which will be solved in this section:
We begin with the squaring property of equalityGiven real numbers a and b, where , then ; given real numbers a and b, we have the following:
In other words, equality is retained if we square both sides of an equation.
The converse, on the other hand, is not necessarily true,
This is important because we will use this property to solve radical equations. Consider a very simple radical equation that can be solved by inspection,
Here we can see that is a solution. To solve this equation algebraically, make use of the squaring property of equality and the fact that when a is nonnegative. Eliminate the square root by squaring both sides of the equation as follows:
As a check, we can see that as expected. Because the converse of the squaring property of equality is not necessarily true, solutions to the squared equation may not be solutions to the original. Hence squaring both sides of an equation introduces the possibility of extraneous solutionsA properly found solution that does not solve the original equation., which are solutions that do not solve the original equation. For example,
This equation clearly does not have a real number solution. However, squaring both sides gives us a solution:
As a check, we can see that For this reason, we must check the answers that result from squaring both sides of an equation.
Example 1
Solve:
Solution:
We can eliminate the square root by applying the squaring property of equality.
Next, we must check.
Answer: The solution is 5.
There is a geometric interpretation to the previous example. Graph the function defined by and determine where it intersects the graph defined by
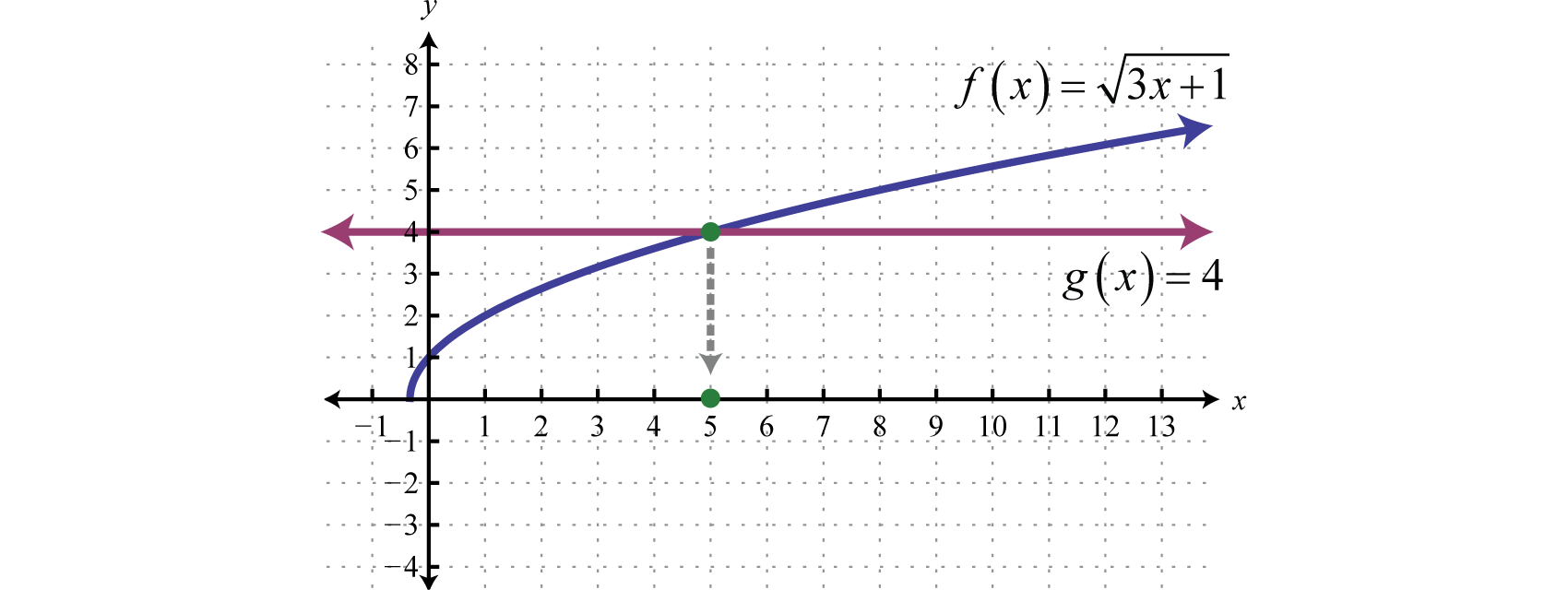
As illustrated, where
Example 2
Solve:
Solution:
Begin by squaring both sides of the equation.
The resulting quadratic equation can be solved by factoring.
Checking the solutions after squaring both sides of an equation is not optional. Use the original equation when performing the check.
After checking, you can see that is an extraneous solution; it does not solve the original radical equation. Disregard that answer. This leaves as the only solution.
Answer: The solution is 7.
Geometrically we can see that is equal to where
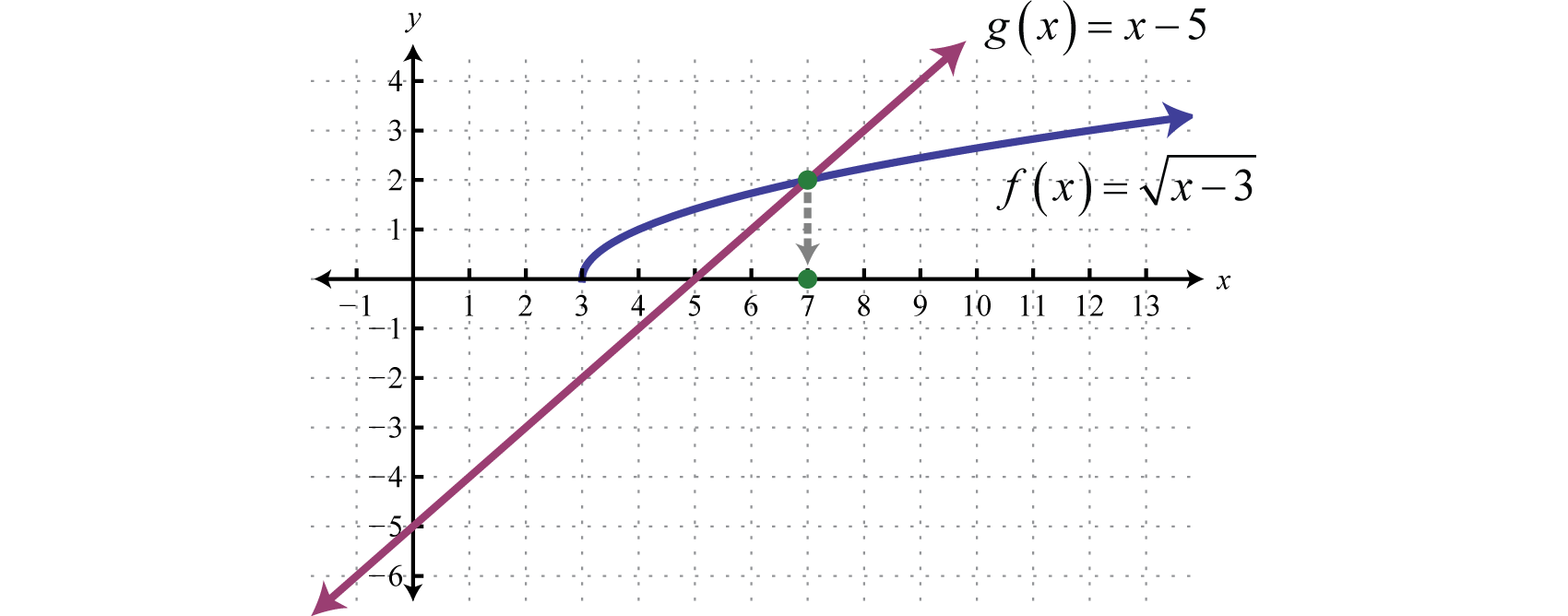
In the previous two examples, notice that the radical is isolated on one side of the equation. Typically, this is not the case. The steps for solving radical equations involving square roots are outlined in the following example.
Example 3
Solve:
Solution:
Step 1: Isolate the square root. Begin by subtracting 2 from both sides of the equation.
Step 2: Square both sides. Squaring both sides eliminates the square root.
Step 3: Solve the resulting equation. Here we are left with a quadratic equation that can be solved by factoring.
Step 4: Check the solutions in the original equation. Squaring both sides introduces the possibility of extraneous solutions; hence the check is required.
After checking, we can see that is an extraneous solution; it does not solve the original radical equation. This leaves as the only solution.
Answer: The solution is 5.
Sometimes there is more than one solution to a radical equation.
Example 4
Solve:
Solution:
Begin by isolating the term with the radical.
Despite the fact that the term on the left side has a coefficient, we still consider it to be isolated. Recall that terms are separated by addition or subtraction operators.
Solve the resulting quadratic equation.
Since we squared both sides, we must check our solutions.
After checking, we can see that both are solutions to the original equation.
Answer: The solutions are ±2.
Sometimes both of the possible solutions are extraneous.
Example 5
Solve:
Solution:
Begin by isolating the radical.
Since we squared both sides, we must check our solutions.
Since both possible solutions are extraneous, the equation has no solution.
Answer: No solution, Ø
The squaring property of equality extends to any positive integer power n. Given real numbers a and b, we have the following:
This is often referred to as the power property of equalityGiven any positive integer n and real numbers a and b where , then . Use this property, along with the fact that , when a is nonnegative, to solve radical equations with indices greater than 2.
Example 6
Solve:
Solution:
Isolate the radical, and then cube both sides of the equation.
Check.
Answer: The solutions are .
It may be the case that the equation has more than one term that consists of radical expressions.
Example 7
Solve:
Solution:
Both radicals are considered isolated on separate sides of the equation.
Check
Answer: The solution is 2.
Example 8
Solve:
Solution:
Eliminate the radicals by cubing both sides.
Check.
Answer: The solutions are
It may not be possible to isolate a radical on both sides of the equation. When this is the case, isolate the radicals, one at a time, and apply the squaring property of equality multiple times until only a polynomial remains.
Example 9
Solve:
Solution:
Begin by isolating one of the radicals. In this case, add to both sides of the equation.
Next, square both sides. Take care to apply the distributive property to the right side.
At this point we have one term that contains a radical. Isolate it and square both sides again.
Check to see if satisfies the original equation
Answer: The solution is
Note: Because , we cannot simply square each term. For example, it is incorrect to square each term as follows.
This is a common mistake and leads to an incorrect result. When squaring both sides of an equation with multiple terms, we must take care to apply the distributive property.
Example 10
Solve:
Solution:
Begin by isolating one of the radicals. In this case, add to both sides of the equation.
Next, square both sides. Take care to apply the distributive property to the right side.
At this point we have one term that contains a radical. Isolate it and square both sides again.
Check.
Answer: The solution is 3.
Key Takeaways
- Solve equations involving square roots by first isolating the radical and then squaring both sides. Squaring a square root eliminates the radical, leaving us with an equation that can be solved using the techniques learned earlier in our study of algebra.
- Squaring both sides of an equation introduces the possibility of extraneous solutions. For this reason, you must check your solutions in the original equation.
- Solve equations involving nth roots by first isolating the radical and then raise both sides to the nth power. This eliminates the radical and results in an equation that may be solved with techniques you have already mastered.
- When more than one radical term is present in an equation, isolate them one at a time, and apply the power property of equality multiple times until only a polynomial remains.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solve for P:
-
Solve for x:
-
Solve for s:
-
Solve for L:
-
Solve for R:
-
Solve for h:
-
Solve for V:
-
Solve for c:
-
The square root of 1 less than twice a number is equal to 2 less than the number. Find the number.
-
The square root of 4 less than twice a number is equal to 6 less than the number. Find the number.
-
The square root of twice a number is equal to one-half of that number. Find the number.
-
The square root of twice a number is equal to one-third of that number. Find the number.
-
The distance d in miles a person can see an object on the horizon is given by the formula where h represents the height in feet of the person’s eyes above sea level. How high must a person’s eyes be to see an object 5 miles away?
-
The current I measured in amperes is given by the formula where P is the power usage measured in watts and R is the resistance measured in ohms. If a light bulb requires 1/2 amperes of current and uses 60 watts of power, then what is the resistance through the bulb?
-
1 second
-
2 seconds
-
second
-
second
-
1 second
-
2 seconds
-
second
-
second
Part A: Solving Radical Equations
Solve
Determine the roots of the given functions. Recall that a root is a value in the domain that results in zero. In other words, find where
Solve for the indicated variable.
The period of a pendulum T in seconds is given by the formula where L represents the length in feet. Calculate the length of a pendulum given the period. Give the exact value and the approximate value rounded to the nearest tenth of a foot.
The time t in seconds, an object is in free fall is given by the formula where s represents the distance it has fallen, in feet. Calculate the distance an object will fall given the amount of time.
-
Discuss reasons why we sometimes obtain extraneous solutions when solving radical equations. Are there ever any conditions where we do not need to check for extraneous solutions? Why or why not?
-
If an equation has multiple terms, explain why squaring all of them is incorrect. Provide an example.
Part B: Discussion Board
Answers
-
49
-
-
1
-
-
Ø
-
-
-
-
1
-
-
3
-
-
-
-
0
-
-
-
-
Ø
-
-
27
-
-
9
-
-
−3
-
-
6
-
-
-
-
2
-
-
7
-
-
2
-
-
−3
-
-
13
-
-
7
-
-
2, 6
-
-
2
-
-
−1, 8
-
-
5
-
-
Ø
-
-
−3, 3
-
-
2, 5
-
-
−4, 4
-
-
-
-
2, 7
-
-
Ø
-
-
10
-
-
−6, −4
-
-
-
-
Ø
-
-
−5, 5
-
-
−9, 3
-
-
-
-
-
-
−1, 1/2
-
-
5, 10
-
-
−7, 7
-
-
-
-
1
-
-
10
-
-
Ø
-
-
3
-
-
−1, 2
-
-
100
-
-
−8
-
-
10
-
-
−13
-
-
-
-
−6, −4
-
-
−2, 2
-
-
1
-
-
−2
-
-
−1
-
-
14
-
-
−9
-
-
-
-
-
-
-
-
-
-
5
-
-
0, 8
-
-
feet
-
-
feet; 0.8 feet
-
-
feet; 0.2 feet
-
-
16 feet
-
-
4 feet
-
-
Answer may vary
-
5.7 Complex Numbers and Their Operations
Learning Objectives
- Define the imaginary unit and complex numbers.
- Add and subtract complex numbers.
- Multiply and divide complex numbers.
Introduction to Complex Numbers
Up to this point the square root of a negative number has been left undefined. For example, we know that is not a real number.
There is no real number that when squared results in a negative number. We begin to resolve this issue by defining the imaginary unitDefined as where , i, as the square root of −1.
To express a square root of a negative number in terms of the imaginary unit i, we use the following property where a represents any non-negative real number:
With this we can write
If , then we would expect that squared will equal −9:
In this way any square root of a negative real number can be written in terms of the imaginary unit. Such a number is often called an imaginary numberA square root of any negative real number..
Example 1
Rewrite in terms of the imaginary unit i.
Solution:
Notation Note: When an imaginary number involves a radical, we place i in front of the radical. Consider the following:
Since multiplication is commutative, these numbers are equivalent. However, in the form , the imaginary unit i is often misinterpreted to be part of the radicand. To avoid this confusion, it is a best practice to place i in front of the radical and use
A complex numberA number of the form where a and b are real numbers. is any number of the form, where a and b are real numbers. Here, a is called the real partThe real number a of a complex number and b is called the imaginary partThe real number b of a complex number . For example, is a complex number with a real part of 3 and an imaginary part of −4. It is important to note that any real number is also a complex number. For example, 5 is a real number; it can be written as with a real part of 5 and an imaginary part of 0. Hence, the set of real numbers, denoted , is a subset of the set of complex numbers, denoted

Complex numbers are used in many fields including electronics, engineering, physics, and mathematics. In this textbook we will use them to better understand solutions to equations such as For this reason, we next explore algebraic operations with them.
Adding and Subtracting Complex Numbers
Adding or subtracting complex numbers is similar to adding and subtracting polynomials with like terms. We add or subtract the real parts and then the imaginary parts.
Example 2
Add:
Solution:
Add the real parts and then add the imaginary parts.
Answer:
To subtract complex numbers, we subtract the real parts and subtract the imaginary parts. This is consistent with the use of the distributive property.
Example 3
Subtract:
Solution:
Distribute the negative sign and then combine like terms.
Answer:
In general, given real numbers a, b, c and d:
Example 4
Simplify:
Solution:
Answer:
In summary, adding and subtracting complex numbers results in a complex number.
Multiplying and Dividing Complex Numbers
Multiplying complex numbers is similar to multiplying polynomials. The distributive property applies. In addition, we make use of the fact that to simplify the result into standard form
Example 5
Multiply:
Solution:
We begin by applying the distributive property.
Answer:
Example 6
Multiply:
Solution:
Answer:
In general, given real numbers a, b, c and d:
Given a complex number , its complex conjugateTwo complex numbers whose real parts are the same and imaginary parts are opposite. If given , then its complex conjugate is is We next explore the product of complex conjugates.
Example 7
Multiply:
Solution:
Answer: 29
In general, the product of complex conjugatesThe real number that results from multiplying complex conjugates: follows:
Note that the result does not involve the imaginary unit; hence, it is real. This leads us to the very useful property
To divide complex numbers, we apply the technique used to rationalize the denominator. Multiply the numerator and denominator by the conjugate of the denominator. The result can then be simplified into standard form
Example 8
Divide:
Solution:
In this example, the conjugate of the denominator is Therefore, we will multiply by 1 in the form
To write this complex number in standard form, we make use of the fact that 13 is a common denominator.
Answer:
Example 9
Divide:
Solution:
Answer:
In general, given real numbers a, b, c and d where c and d are not both 0:
Example 10
Divide:
Solution:
Here we can think of and thus we can see that its conjugate is
Because the denominator is a monomial, we could multiply numerator and denominator by 1 in the form of and save some steps reducing in the end.
Answer:
When multiplying and dividing complex numbers we must take care to understand that the product and quotient rules for radicals require that both a and b are positive. In other words, if and are both real numbers then we have the following rules.
For example, we can demonstrate that the product rule is true when a and b are both positive as follows:
However, when a and b are both negative the property is not true.
Here and both are not real numbers and the product rule for radicals fails to produce a true statement. Therefore, to avoid some common errors associated with this technicality, ensure that any complex number is written in terms of the imaginary unit i before performing any operations.
Example 11
Multiply:
Solution:
Begin by writing the radicals in terms of the imaginary unit i.
Now the radicands are both positive and the product rule for radicals applies.
Answer:
Example 12
Multiply:
Solution:
Begin by writing the radicals in terms of the imaginary unit and then distribute.
Answer:
In summary, multiplying and dividing complex numbers results in a complex number.
Key Takeaways
- The imaginary unit i is defined to be the square root of negative one. In other words, and
- Complex numbers have the form where a and b are real numbers.
- The set of real numbers is a subset of the complex numbers.
- The result of adding, subtracting, multiplying, and dividing complex numbers is a complex number.
- The product of complex conjugates, and , is a real number. Use this fact to divide complex numbers. Multiply the numerator and denominator of a fraction by the complex conjugate of the denominator and then simplify.
- Ensure that any complex number is written in terms of the imaginary unit i before performing any operations.
Topic Exercises
Part A: Introduction to Complex Numbers
Rewrite in terms of imaginary unit i.
Write the complex number in standard form
Given that compute the following powers of
Part B: Adding and Subtracting Complex Numbers
Perform the operations.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Show that both and satisfy
-
Show that both and satisfy
-
Show that both and satisfy
-
Show that both and satisfy
-
Show that 3, , and are all solutions to
-
Show that −2, , and are all solutions to
Part C: Multiplying and Dividing Complex Numbers
Perform the operations.
Given that compute the following powers of
Perform the operations and simplify.
-
Research and discuss the history of the imaginary unit and complex numbers.
-
How would you define and why?
-
Research what it means to calculate the absolute value of a complex number Illustrate your finding with an example.
-
Explore the powers of i. Look for a pattern and share your findings.
Part D: Discussion Board.
Answers
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
-
-
20
-
-
-
-
-
-
-
-
-
-
22
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
-
−3
-
-
-
-
-
-
-
-
Proof
-
-
Proof
-
-
Proof
-
-
Answer may vary
-
-
Answer may vary
-
5.8 Review Exercises and Sample Exam
Review Exercises
-
-
-
-
-
-
-
-
-
Given , find and
-
Given , find and
-
Determine the domain of the function defined by
-
Determine the domain of the function defined by
-
-
-
-
-
-
-
-
Roots and Radicals
Simplify.
Simplify.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The period T in seconds of a pendulum is given by the formula where L represents the length in feet of the pendulum. Calculate the period of a pendulum that is feet long. Give the exact answer and the approximate answer to the nearest hundredth of a second.
-
The time in seconds an object is in free fall is given by the formula where s represents the distance in feet the object has fallen. How long does it take an object to fall 28 feet? Give the exact answer and the approximate answer to the nearest tenth of a second.
-
Find the distance between (−5, 6) and (−3,−4).
-
Find the distance between and
-
(−4,5), (−3,−1), and (3,0)
-
(−1,−1), (1,3), and (−6,1)
Simplifying Radical Expressions
Simplify.
Simplify. (Assume all variable expressions are nonzero.)
Determine whether or not the three points form a right triangle. Use the Pythagorean theorem to justify your answer.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Calculate the perimeter of the triangle formed by the following set of vertices:
-
Calculate the perimeter of the triangle formed by the following set of vertices:
Adding and Subtracting Radical Expressions
Simplify. Assume all radicands containing variables are nonnegative.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The base of a triangle measures units and the height measures units. Find the area of the triangle.
-
If each side of a square measures units, find the area of the square.
Multiplying and Dividing Radical Expressions
Multiply.
Divide. Assume all variables represent nonzero numbers and rationalize the denominator where appropriate.
Rational Exponents
Express in radical form.
Write as a radical and then simplify.
Perform the operations and simplify. Leave answers in exponential form.
Perform the operations with mixed indices.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solve for g:
-
Solve for x:
-
The period in seconds of a pendulum is given by the formula where L represents the length in feet of the pendulum. Find the length of a pendulum that has a period of seconds. Find the exact answer and the approximate answer rounded off to the nearest tenth of a foot.
-
The outer radius of a spherical shell is given by the formula where V represents the inner volume in cubic centimeters. If the outer radius measures 8 centimeters, find the inner volume of the sphere.
-
The speed of a vehicle before the brakes are applied can be estimated by the length of the skid marks left on the road. On dry pavement, the speed v in miles per hour can be estimated by the formula , where d represents the length of the skid marks in feet. Estimate the length of a skid mark if the vehicle is traveling 30 miles per hour before the brakes are applied.
-
Find the real root of the function defined by
Solving Radical Equations
Solve.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Show that both and satisfy
-
Show that both and satisfy
Complex Numbers and Their Operations
Write the complex number in standard form
Perform the operations.
Answers
-
−11
-
-
-
-
5
-
-
-
-
;
-
-
-
-
-
-
-
-
−9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
seconds; 1.76 seconds
-
-
units
-
-
Right triangle
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
units
-
-
-
-
-
-
22
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
square units
-
-
-
-
-
-
4
-
-
-
-
1/27
-
-
36
-
-
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
25
-
-
21
-
-
9
-
-
4
-
-
4
-
-
7
-
-
1
-
-
-
-
-
-
-
-
9
-
-
9
-
-
1
-
-
12
-
-
-
-
feet; 1.8 feet
-
-
37.5 feet
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
13
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Answer may vary
-
Sample Exam
-
-
-
Calculate the distance between and
-
The time in seconds an object is in free fall is given by the formula where s represents the distance in feet that the object has fallen. If a stone is dropped into a 36-foot pit, how long will it take to hit the bottom of the pit?
-
-
-
-
-
-
-
-
Simplify:
-
Express in radical form:
-
-
-
-
-
-
-
-
The time in seconds an object is in free fall is given by the formula where s represents the distance in feet that the object has fallen. If a stone is dropped into a pit and it takes 4 seconds to reach the bottom, how deep is the pit?
-
The width in inches of a container is given by the formula where V represents the inside volume in cubic inches of the container. What is the inside volume of the container if the width is 6 inches?
-
-
-
Simplify. (Assume all variables are positive.)
Perform the operations and simplify. (Assume all variables are positive and rationalize the denominator where appropriate.)
Simplify. Assume all variables are nonzero and leave answers in exponential form.
Solve.
Perform the operations and write the answer in standard form.
Answers
-
-
-
units
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Ø
-
-
256 feet
-
-
-
-




