This is “Rational Functions: Multiplication and Division”, section 4.5 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
4.5 Rational Functions: Multiplication and Division
Learning Objectives
- Identify restrictions to the domain of a rational function.
- Simplify rational functions.
- Multiply and divide rational functions.
Identifying Restrictions and Simplifying Rational Functions
Rational functionsFunctions of the form , where and are polynomials and have the form where and are polynomials and The domain of a rational functionThe set of real numbers for which the rational function is defined. consists of all real numbers x except those where the denominator RestrictionsThe set of real numbers for which a rational function is not defined. are the real numbers for which the expression is not defined. We often express the domain of a rational function in terms of its restrictions. For example, consider the function
which can be written in factored form
Because rational expressions are undefined when the denominator is 0, we wish to find the values for x that make it 0. To do this, apply the zero-product property. Set each factor in the denominator equal to 0 and solve.
Therefore, the original function is defined for any real number except 2 and 3. We can express its domain using notation as follows:
The restrictions to the domain of a rational function are determined by the denominator. Once the restrictions are determined we can cancel factors and obtain an equivalent function as follows:

It is important to note that 1 is not a restriction to the domain because the expression is defined as 0 when the numerator is 0. In fact, is a root. This function is graphed below:
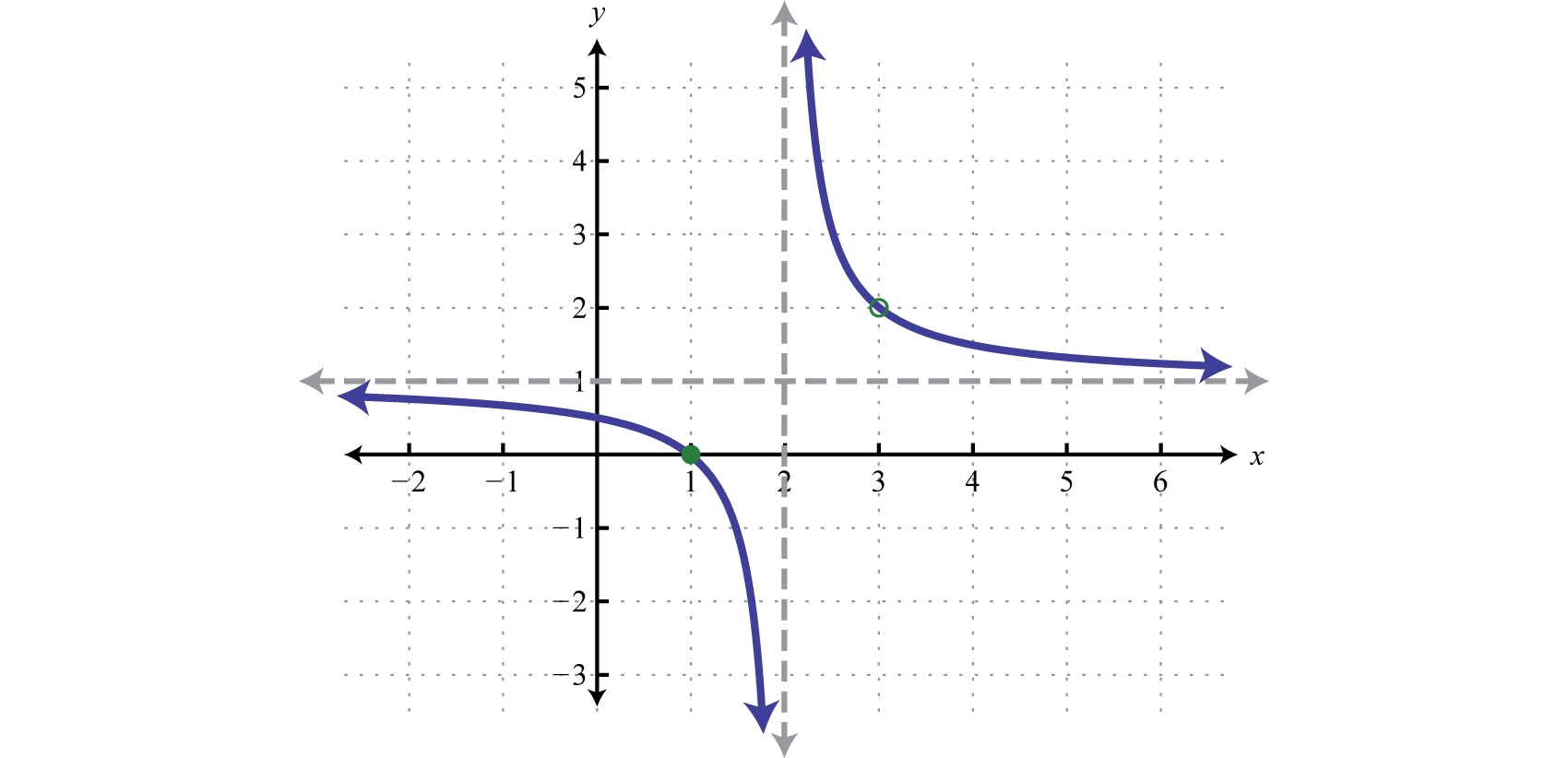
Notice that there is a vertical asymptote at the restriction and the graph is left undefined at the restriction as indicated by the open dot, or hole, in the graph. Graphing rational functions in general is beyond the scope of this textbook. However, it is useful at this point to know that the restrictions are an important part of the graph of rational functions.
Example 1
State the restrictions and simplify:
Solution:
In this example, the function is undefined where x is 0.
Therefore, the domain consists of all real numbers x, where With this understanding, we can simplify by reducing the rational expression to lowest terms. Cancel common factors.
Answer: , where
Example 2
State the restrictions and simplify:
Solution:
First, factor the numerator and denominator.
Any x-value that makes the denominator zero is a restriction. To find the restrictions, first set the denominator equal to zero and then solve
Therefore, With this understanding, we can cancel any common factors.
Answer: , where
We define the opposite of a polynomial P to be −P. Finding the opposite of a polynomial requires the application of the distributive property. For example, the opposite of the polynomial is written as
This leads us to the opposite binomial propertyIf given a binomial , then the opposite is , Care should be taken not to confuse this with the fact that This is the case because addition is commutative. In general,
Also, it is important to recall that
In other words, a negative fraction is shown by placing the negative sign in either the numerator, in front of the fraction bar, or in the denominator. Generally, negative denominators are avoided.
Example 3
State the restrictions and simplify:
Solution:
Begin by factoring the numerator and denominator.
Answer: , where
It is important to remember that we can only cancel factors of a product. A common mistake is to cancel terms. For example,
In some examples, we will make a broad assumption that the denominator is nonzero. When we make that assumption, we do not need to determine the restrictions.
Example 4
Simplify: (Assume all denominators are nonzero.)
Solution:
Factor the numerator by grouping. Factor the denominator using the formula for a difference of squares.
Next, cancel common factors.
Note: When the entire numerator or denominator cancels out a factor of 1 always remains.
Answer:
Example 5
Given , simplify
Solution:
Begin by calculating
Next, substitute into the quotient that is to be simplified.
Answer: , where
An important quantity in higher level mathematics is the difference quotientThe mathematical quantity , where , which represents the slope of a secant line through a function f.:
This quantity represents the slope of the line connecting two points on the graph of a function. The line passing through the two points is called a secant lineLine that intersects two points on the graph of a function..

Calculating the difference quotient for many different functions is an important skill to learn in intermediate algebra. We will encounter this quantity often as we proceed in this textbook. When calculating the difference quotient we assume the denominator is nonzero.
Example 6
Given , simplify
Solution:
Answer:
Multiplying and Dividing Rational Functions
When multiplying fractions, we can multiply the numerators and denominators together and then reduce. Multiplying rational expressions is performed in a similar manner. In general, given polynomials P, Q, R, and S, where and , we have
The restrictions to the domain of a product consist of the restrictions of each function.
Example 7
Given and , find and determine the restrictions to the domain.
Solution:
In this case, the domain of consists of all real numbers except 5, and the domain of consists of all real numbers except Therefore, the domain of the product consists of all real numbers except 5 and Multiply the functions and then simplify the result.
Answer: , where
To divide two fractions, we multiply by the reciprocal of the divisor. Dividing rational expressions is performed in a similar manner. In general, given polynomials P, Q, R, and S, where , , and , we have
The restrictions to the domain of a quotient will consist of the restrictions of each function as well as the restrictions on the reciprocal of the divisor.
Example 8
Given and , find and determine the restrictions.
Solution:
In this case, the domain of consists of all real numbers except −3 and 7, and the domain of consists of all real numbers except 7 and −7. In addition, the reciprocal of has a restriction of −3 and Therefore, the domain of this quotient consists of all real numbers except −3, , and ±7.
Answer: , where
Recall that multiplication and division operations are to be performed from left to right.
Example 9
Simplify: (Assume all denominators are nonzero.)
Solution:
Begin by replacing the factor that is to be divided by multiplication of its reciprocal.
Answer:
Try this! Given and , calculate and determine the restrictions.
Answer: , where
If a cost function represents the cost of producing x units, then the average costThe total cost divided by the number of units produced, which can be represented by , where is a cost function. is the cost divided by the number of units produced.
Example 10
A manufacturer has determined that the cost in dollars of producing sweaters is given by , where x represents the number of sweaters produced daily. Determine the average cost of producing 100, 200, and 300 sweaters per day.
Solution:
Set up a function representing the average cost.
Next, calculate , , and
Answer: The average cost of producing 100 sweaters per day is $10.00 per sweater. If 200 sweaters are produced, the average cost per sweater is $5.00. If 300 are produced, the average cost per sweater is $4.00.
Key Takeaways
- Simplifying rational expressions is similar to simplifying fractions. First, factor the numerator and denominator and then cancel the common factors. Rational expressions are simplified if there are no common factors other than 1 in the numerator and the denominator.
- Simplified rational functions are equivalent for values in the domain of the original function. Be sure to state the restrictions unless the problem states that the denominators are assumed to be nonzero.
- After multiplying rational expressions, factor both the numerator and denominator and then cancel common factors. Make note of the restrictions to the domain. The values that give a value of 0 in the denominator for all expressions are the restrictions.
- To divide rational expressions, multiply the numerator by the reciprocal of the divisor.
- The restrictions to the domain of a product consist of the restrictions to the domain of each factor.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Given , simplify
-
Given , simplify
-
Given , simplify
-
Given , simplify
-
Given , simplify
-
Given , simplify
-
-
-
-
-
-
-
-
-
-
Part A: Simplifying Rational Functions
Simplify the function and state its domain using interval notation.
State the restrictions and simplify the given rational expressions.
Simplify the given rational expressions. Assume all variable expressions in the denominator are nonzero.
Given the function, simplify the rational expression.
For the given function, simplify the difference quotient
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A manufacturer has determined that the cost in dollars of producing bicycles is given by , where x represents the number of bicycles produced weekly. Determine the average cost of producing 50, 100, and 150 bicycles per week.
-
The cost in dollars of producing custom lighting fixtures is given by the function , where x represents the number of fixtures produced in a week. Determine the average cost per unit if 20, 40, and 50 units are produced in a week.
-
A manufacturer has determined that the cost in dollars of producing electric scooters is given by the function , where x represents the number of scooters produced in a month. Determine the average cost per scooter if 50 are produced in a month.
-
The cost in dollars of producing a custom injected molded part is given by , where n represents the number of parts produced. Calculate the average cost of each part if 2,500 custom parts are ordered.
-
The cost in dollars of an environmental cleanup is given by the function , where p represents the percentage of the area to be cleaned up . Use the function to determine the cost of cleaning up 50% of an affected area and the cost of cleaning up 80% of the area.
-
The value of a new car is given by the function where t represents the age of the car in years. Determine the value of the car when it is 6 years old.
Part B: Multiplying and Dividing Rational Functions
Simplify the product and state its domain using interval notation.
Simplify the quotient and state its domain using interval notation.
Multiply or divide as indicated, state the restrictions, and simplify.
Perform the operations and simplify. Assume all variable expressions in the denominator are nonzero.
-
Describe the restrictions to the rational expression . Explain.
-
Describe the restrictions to the rational expression . Explain.
-
Explain why is a restriction to
-
Explain to a beginning algebra student why we cannot cancel x in the rational expression
-
Research and discuss the importance of the difference quotient. What does it represent and in what subject does it appear?
Part D: Discussion Board
Answers
-
;
Domain:
-
-
; Domain:
-
-
; Domain:
-
-
; Domain:
-
-
; Domain:
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
, where
-
-
, where
-
-
, where
-
-
5
-
-
-
-
-
-
-
-
-
-
; Domain:
-
-
; Domain:
-
-
; Domain:
-
-
; Domain:
-
-
; Domain:
-
-
; Domain:
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
-
-
-
-
-
-
-
-
-
-
If 50 bicycles are produced, the average cost per bicycle is $148. If 100 are produced, the average cost is $111. If 150 bicycles are produced, the average cost is $115.33.
-
-
If 50 scooters are produced, the average cost of each is $490.
-
-
A 50% cleanup will cost $25,000. An 80% cleanup will cost $100,000.
-
-
Answer may vary
-
-
Answer may vary
-
-
Answer may vary




