This is “Algebra of Functions”, section 4.1 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
4.1 Algebra of Functions
Learning Objectives
- Identify and evaluate polynomial functions.
- Add and subtract functions.
- Multiply and divide functions.
- Add functions graphically.
Polynomial Functions
Any polynomial with one variable is a function and can be written in the form
Here represents any real number and n represents any whole number. The degree of a polynomial with one variable is the largest exponent of all the terms. Typically, we arrange terms of polynomials in descending order based on their degree and classify them as follows:
In this textbook, we call any polynomial with degree higher than 3 an nth-degree polynomial. For example, if the degree is 4, we call it a fourth-degree polynomial; if the degree is 5, we call it a fifth-degree polynomial, and so on.
Example 1
Given , find and
Solution:
Replace each instance of x with the value given inside the parentheses.
|
We can write and Remember that and so we can interpret these results on the graph as follows:
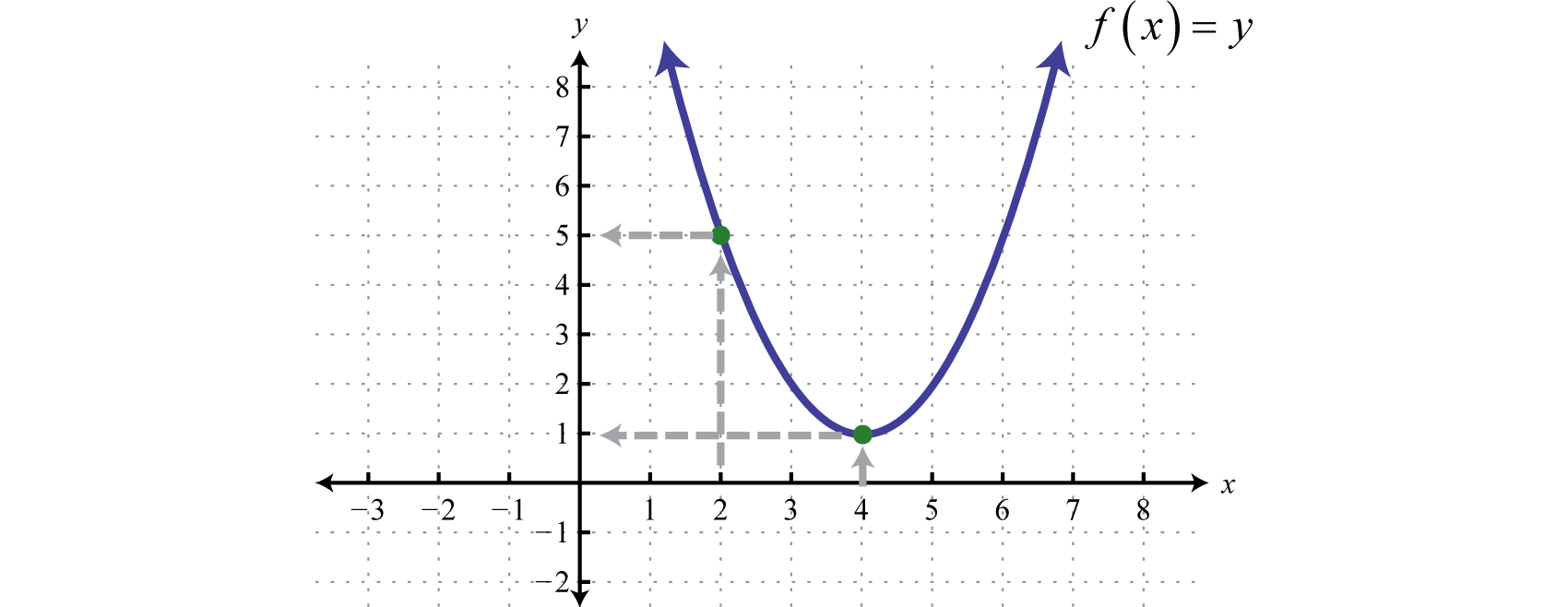
Answer: ;
Often we will be asked to evaluate polynomials for algebraic expressions.
Example 2
Given , find and
Solution:
Replace x with the expressions given inside the parentheses.
Answer: and
The height of an object launched upward, ignoring the effects of air resistance, can be modeled with the following quadratic function:
With this formula, the height can be calculated at any given time t after the object is launched. The letter g represents acceleration due to gravity on the surface of the Earth, which is 32 feet per second squared (or, using metric units, g = 9.8 meters per second squared). The variable , pronounced “v-naught,” or sometimes “v-zero,” represents the initial velocity of the object, and represents the initial height from which the object was launched.
Example 3
An object is launched from the ground at a speed of 64 feet per second. Write a function that models the height of the object and use it to calculate the objects height at 1 second and at 3.5 seconds.
Solution:
We know that the acceleration due to gravity is feet per second squared and we are given the initial velocity feet per second. Since the object is launched from the ground, the initial height is feet. Create the mathematical model by substituting these coefficients into the following formula:
Use this model to calculate the height of the object at 1 second and 3.5 seconds.
Answer: ; At 1 second the object is at a height of 48 feet, and at 3.5 seconds it is at a height of 28 feet.
Try this! An object is dropped from a height of 6 meters. Write a function that models the height of the object and use it to calculate the object’s height 1 second after it is dropped.
Answer: ; At 1 second the object is at a height of 1.1 meters.
Adding and Subtracting Functions
The notation used to indicate additionAdd functions as indicated by the notation: and subtractionSubtract functions as indicated by the notation: of functions follows:
When using function notation, be careful to group the entire function and add or subtract accordingly.
Example 4
Given and , find and
Solution:
The notation indicates that we should add the given expressions.
The notation indicates that we should subtract the given expressions. When subtracting, the parentheses become very important. Recall that we can eliminate them after applying the distributive property.
Answer: and
We may be asked to evaluate the sum or difference of two functions. We have the option to first find the sum or difference in general and then use the resulting function to evaluate for the given variable, or evaluate each first and then find the sum or difference.
Example 5
Evaluate given and
Solution:
First, find
Therefore,
Next, substitute 3 in for the variable x.
Hence
Alternate Solution: Since , we can find and and then subtract the results.
|
|
Therefore,
Notice that we obtain the same answer.
Answer:
Note: If multiple values are to be evaluated, it is best to find the sum or difference in general first and then use it to evaluate.
Multiplying and Dividing Functions
The notation used to indicate multiplicationMultiply functions as indicated by the notation: and divisionDivide functions as indicated by the notation: , where of functions follows:
Multiplication of functions: |
|
Division of functions: |
Example 6
Given and , find and
Solution:
The notation indicates that we should multiply. Apply the distributive property and simplify.
The notation indicates that we should divide. For this quotient, assume
Answer: and where
Example 7
Given and , evaluate and
Solution:
Begin by finding
Therefore , and we have,
Answer: and
Adding Functions Graphically
Here we explore the geometry of adding functions. One way to do this is to use the fact that Add the functions together using x-values for which both and are defined.
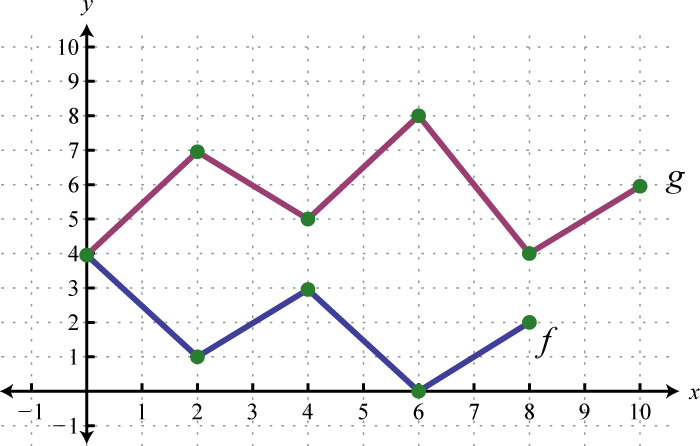
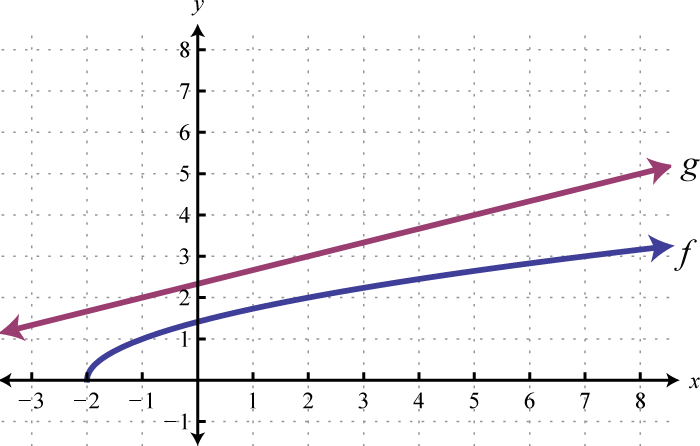
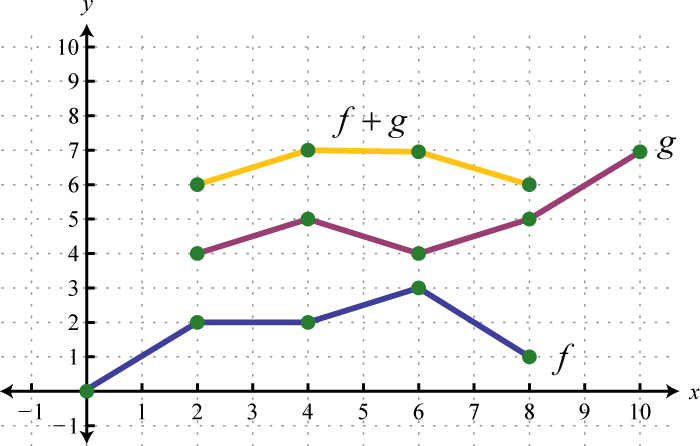
Example 8
Use the graphs of and to graph Also, give the domain of
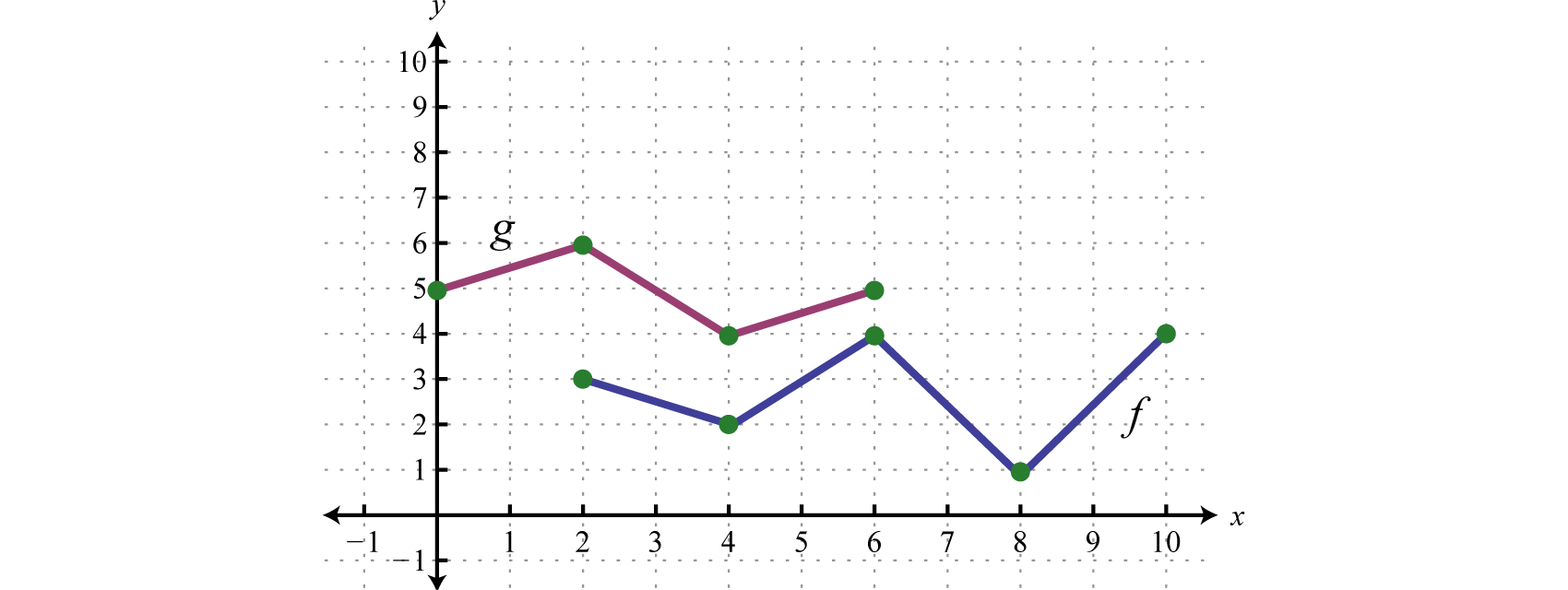
Solution:
In this case, both functions are defined for x-values between 2 and 6. We will use 2, 4, and 6 as representative values in the domain of to sketch its graph.
Sketch the graph of using the three ordered pair solutions , , and

Answer: graphed above has domain
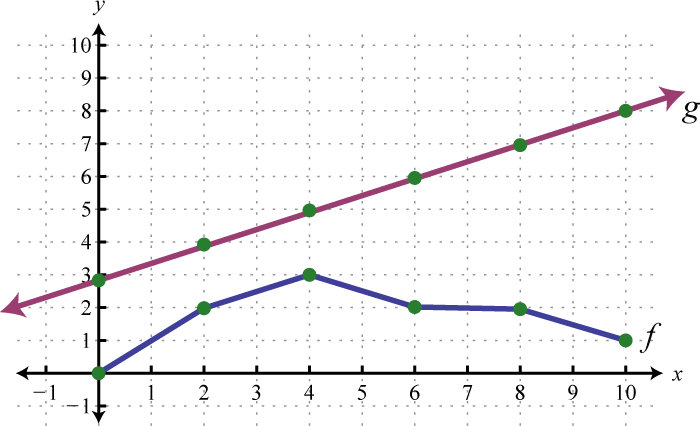
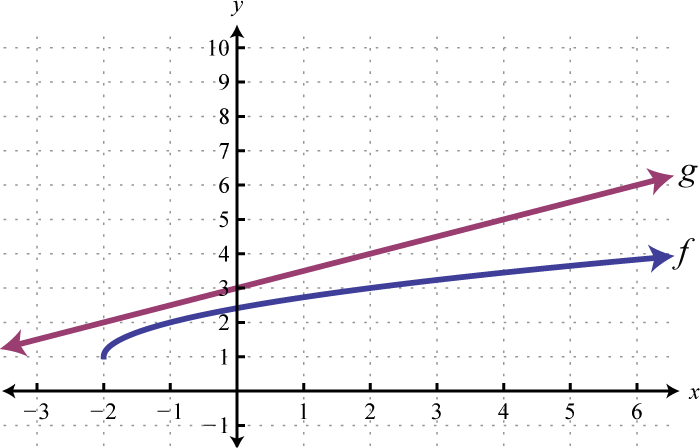
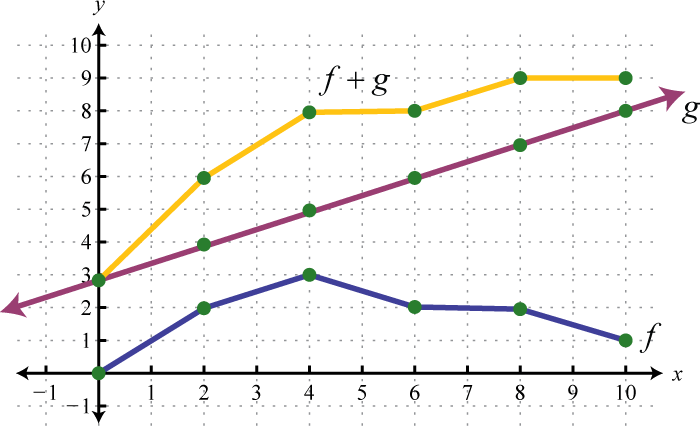
Example 9
Use the graphs of and to graph Also, give the domain of
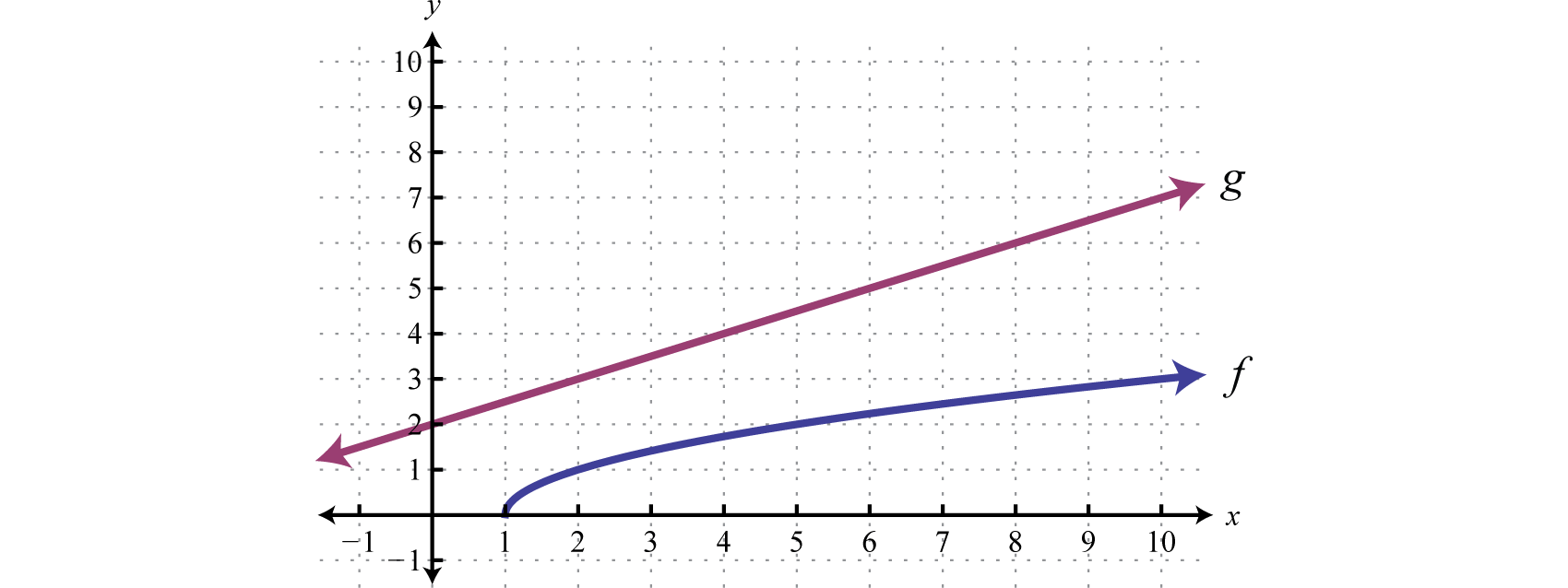
Solution:
Another way to add nonnegative functions graphically is to copy the line segment formed from the x-axis to one of the functions onto the other as illustrated below.
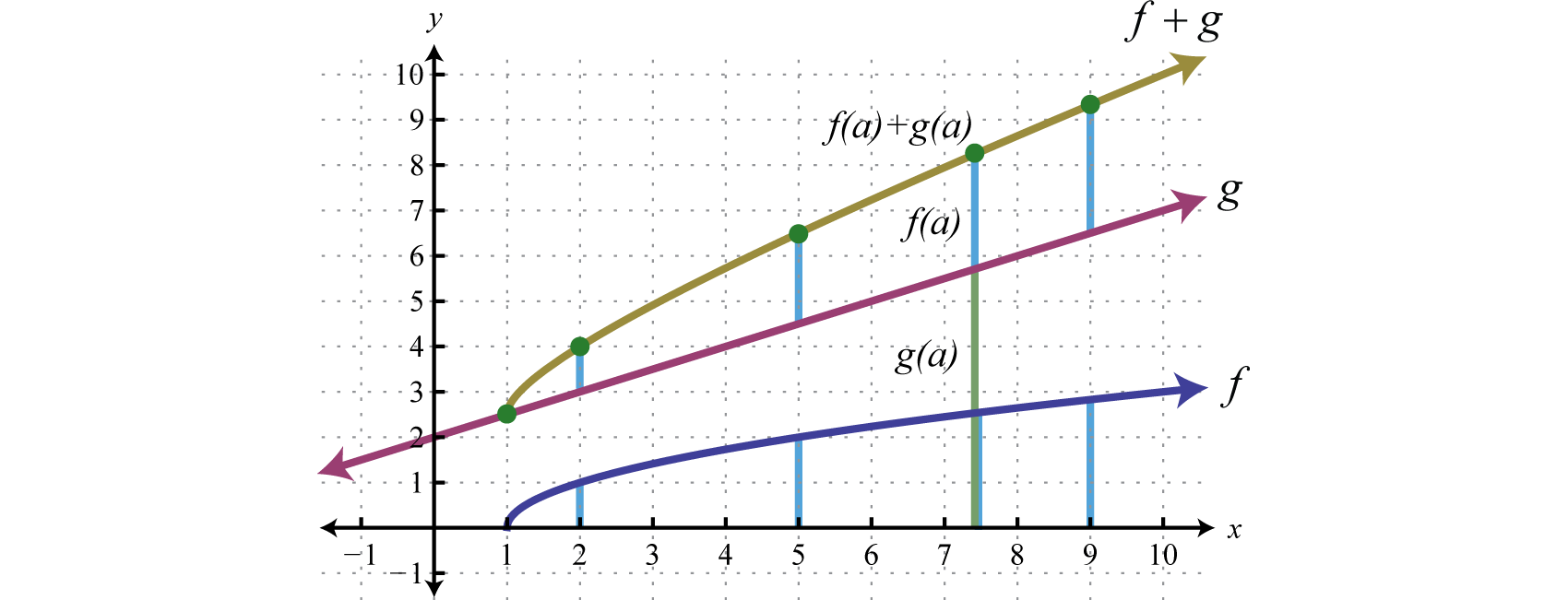
The line segment from the x-axis to the function represents Copy this line segment onto the other function over the same point; the endpoint represents Doing this for a number of points allows us to obtain a quick sketch of the combined graph. In this example, the domain of is limited to the x-values for which is defined.
Answer: Domain:
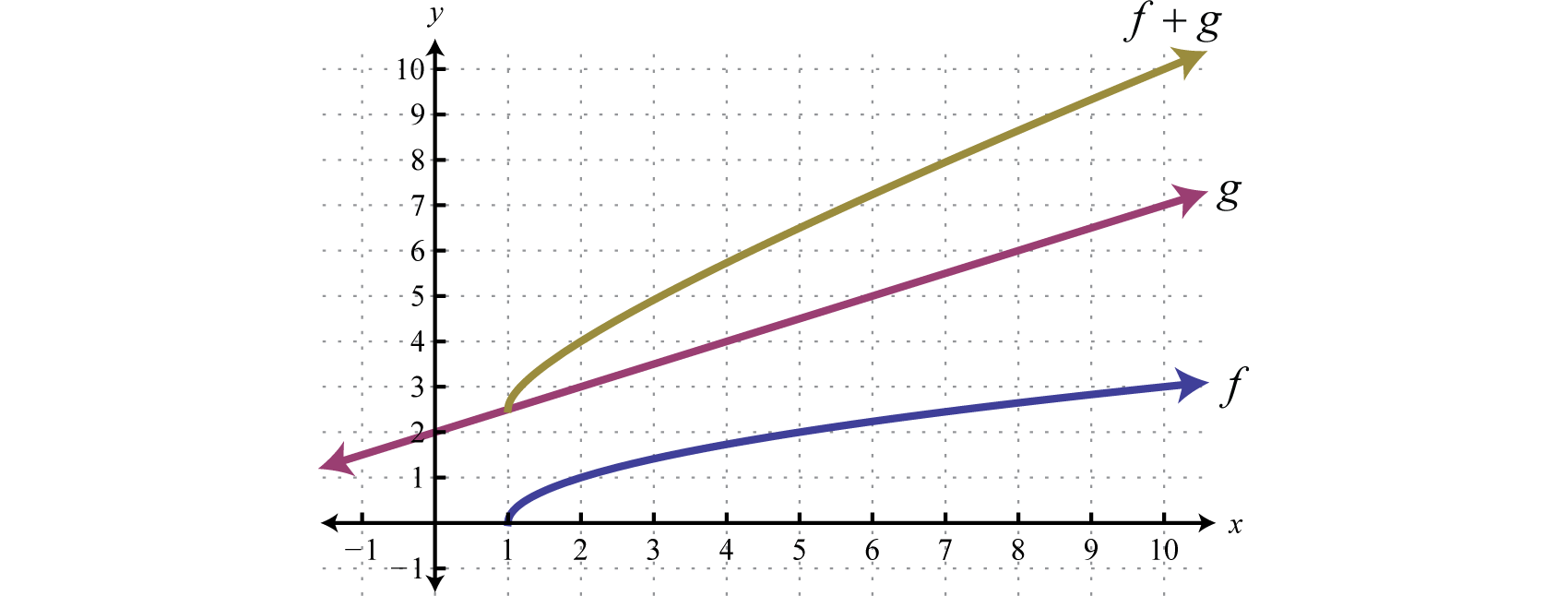
In general, the domain of is the intersection of the domain of with the domain of In fact, this is the case for all of the arithmetic operations with an extra consideration for division. When dividing functions, we take extra care to remove any values that make the denominator zero. This will be discussed in more detail as we progress in algebra.
Key Takeaways
- Any polynomial with one variable is a function and can be written in the form The degree of the polynomial is the largest exponent of all the terms.
- Use function notation to streamline the evaluating process. Substitute the value or expression inside the parentheses for each instance of the variable.
- The notation indicates that we should add
- The notation indicates that we should subtract
- The notation indicates that we should multiply
- The notation indicates that we should divide
- The domain of the function that results from these arithmetic operations is the intersection of the domain of each function. The domain of a quotient is further restricted to values that do not evaluate to zero in the denominator.
Topic Exercises
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , and
-
Given , find and
-
Given , find and
-
Given , find and
-
Given , find and
-
Given , find and
-
Given , find and
-
Given , find and
-
Given , find and
-
-
-
-
-
Find , , and
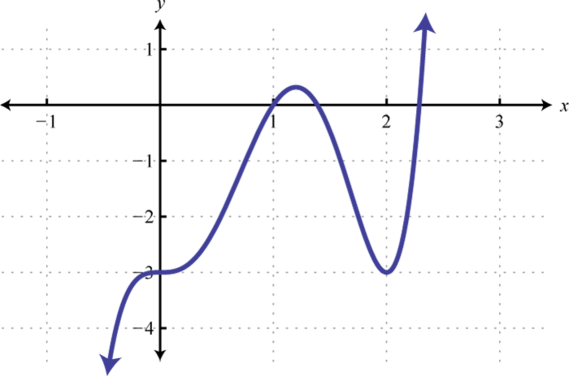
-
Find , , and
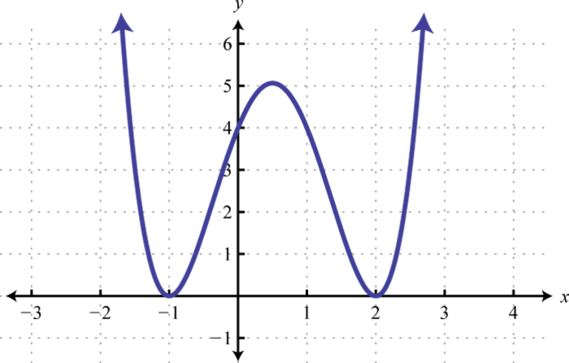
-
Find , , and
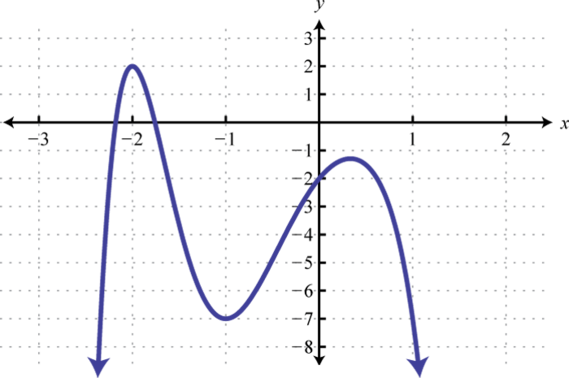
-
Find , , and
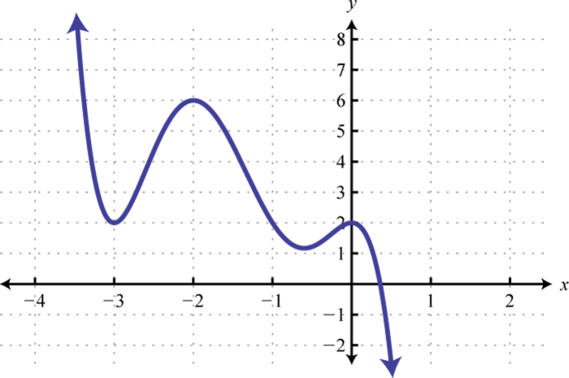
-
A projectile is launched upward from the ground at a speed of 48 feet per second. Write a function that models the height of the projectile and use it to calculate the height every 1/2 second after launch. Sketch a graph that shows the height of the projectile with respect to time.
-
An object is tossed upward from a 48-foot platform at a speed of 32 feet per second. Write a function that models the height of the object and use it to calculate the height every 1/2 second after the object is tossed. Sketch a graph that shows the height of the object with respect to time.
-
An object is dropped from a 128-foot bridge. Write a function that models the height of the object, and use it to calculate the height at 1 second and 2 seconds after it has been dropped.
-
An object is dropped from a 500-foot building. Write a function that models the height of the object, and use it to calculate the distance the object falls in the 1st second, 2nd second, and the 3rd second.
-
A bullet is fired straight up into the air at 320 meters per second. Ignoring the effects of air friction, write a function that models the height of the bullet, and use it to calculate the bullet’s height 1 minute after it was fired into the air.
-
A book is dropped from a height of 10 meters. Write a function that gives the height of the book, and use it to determine how far it will fall in 1¼ seconds.
Part A: Polynomial Functions
Evaluate.
Given the function calculate
Given the graph of the polynomial function find the function values.
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Part B: Adding and Subtracting Functions
Given functions and , find and
Given and , evaluate the following.
Given the graphs of and , evaluate the following.
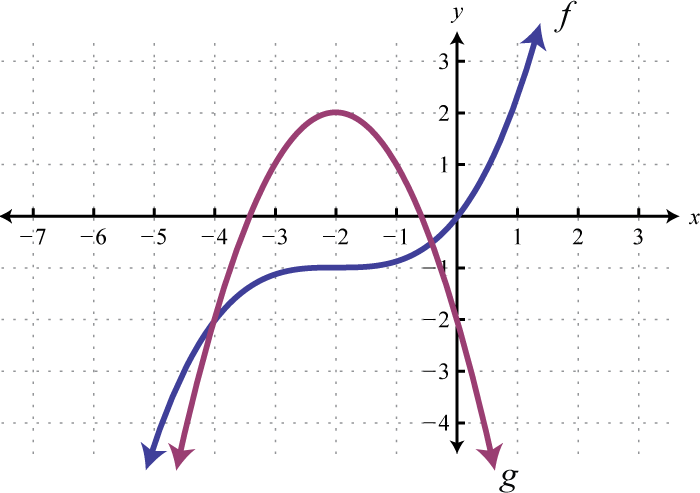
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The revenue in dollars from selling MP3 players is given by the function , where n represents the number of units sold . The cost in dollars of producing the MP3 players is given by the formula where n represents the number of units produced. Write a function that models the profit of producing and selling n MP3 players. Use the function to determine the profit generated from producing and selling 225 MP3 players. Recall that profit equals revenues less costs.
-
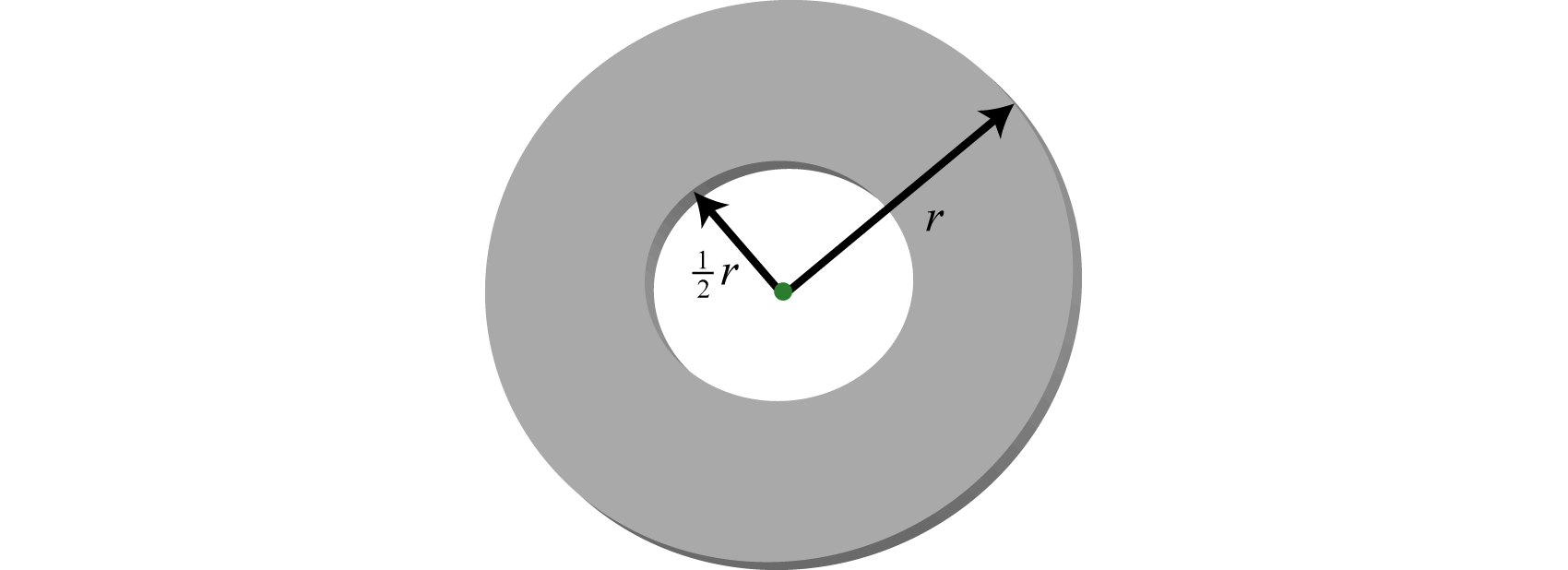
The inner radius of a washer is that of the outer radius.
Part C: Multiplying and Dividing Functions
Given and , find
Given and , find (Assume all expressions in the denominator are nonzero.)
Given and evaluate the following.
Given the graphs of and evaluate the following.
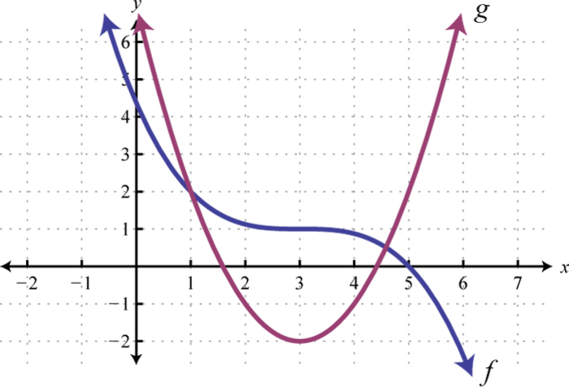
Given , , and , find the following. (Assume all expressions in the denominator are nonzero.)
Part D: Adding Functions Geometrically
Use the graphs of and to graph Also, give the domain of
-
Which arithmetic operations on functions are commutative? Explain.
-
Explore ways we can add functions graphically if they happen to be negative.
Part E: Discussion Board
Answers
-
; ;
-
-
; ;
-
-
; ;
-
-
; ;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
-
-
-
-
; ;
-
-
; ;
-
-
;

-
-
; At 1 second the object’s height is 112 feet and at 2 seconds its height is 64 feet.
-
-
; 1,560 meters
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
11
-
-
−27
-
-
27
-
-
−10
-
-
−4
-
-
1
-
-
−2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
50
-
-
15
-
-
0
-
-
25
-
-
−2
-
-
0
-
-
4
-
-
-
-
-
-
-
-
-
-
; $9,881.25
-
-
Answer may vary
-