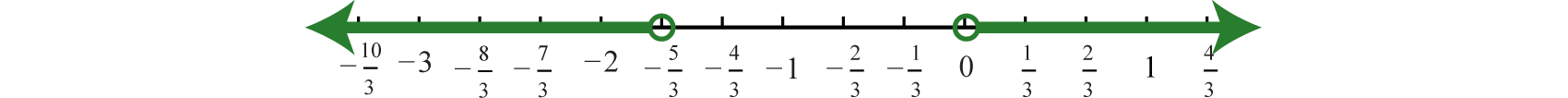This is “Solving Absolute Value Equations and Inequalities”, section 2.6 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
2.6 Solving Absolute Value Equations and Inequalities
Learning Objectives
- Review the definition of absolute value.
- Solve absolute value equations.
- Solve absolute value inequalities.
Absolute Value Equations
Recall that the absolute valueThe distance from the graph of a number a to zero on a number line, denoted of a real number a, denoted , is defined as the distance between zero (the origin) and the graph of that real number on the number line. For example, and
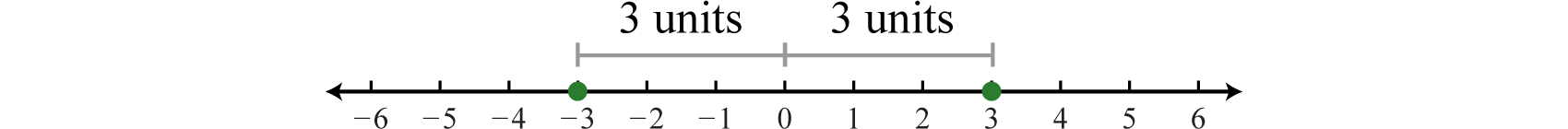
In addition, the absolute value of a real number can be defined algebraically as a piecewise function.
Given this definition, and Therefore, the equation has two solutions for x, namely {±3}. In general, given any algebraic expression X and any positive number p:
In other words, the argument of the absolute valueThe number or expression inside the absolute value. X can be either positive or negative p. Use this theorem to solve absolute value equations algebraically.
Example 1
Solve:
Solution:
In this case, the argument of the absolute value is and must be equal to 3 or −3.
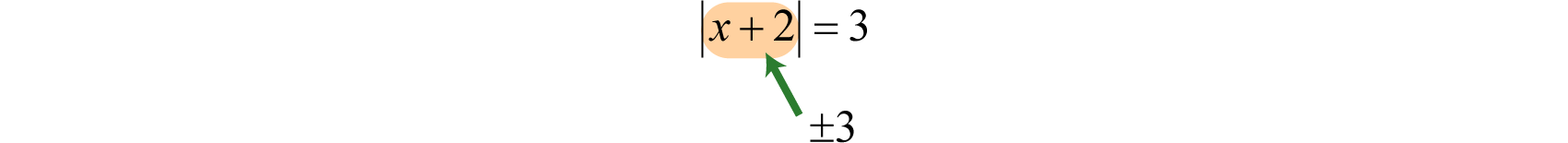
Therefore, to solve this absolute value equation, set equal to ±3 and solve each linear equation as usual.
Answer: The solutions are −5 and 1.
To visualize these solutions, graph the functions on either side of the equal sign on the same set of coordinate axes. In this case, is an absolute value function shifted two units horizontally to the left, and is a constant function whose graph is a horizontal line. Determine the x-values where
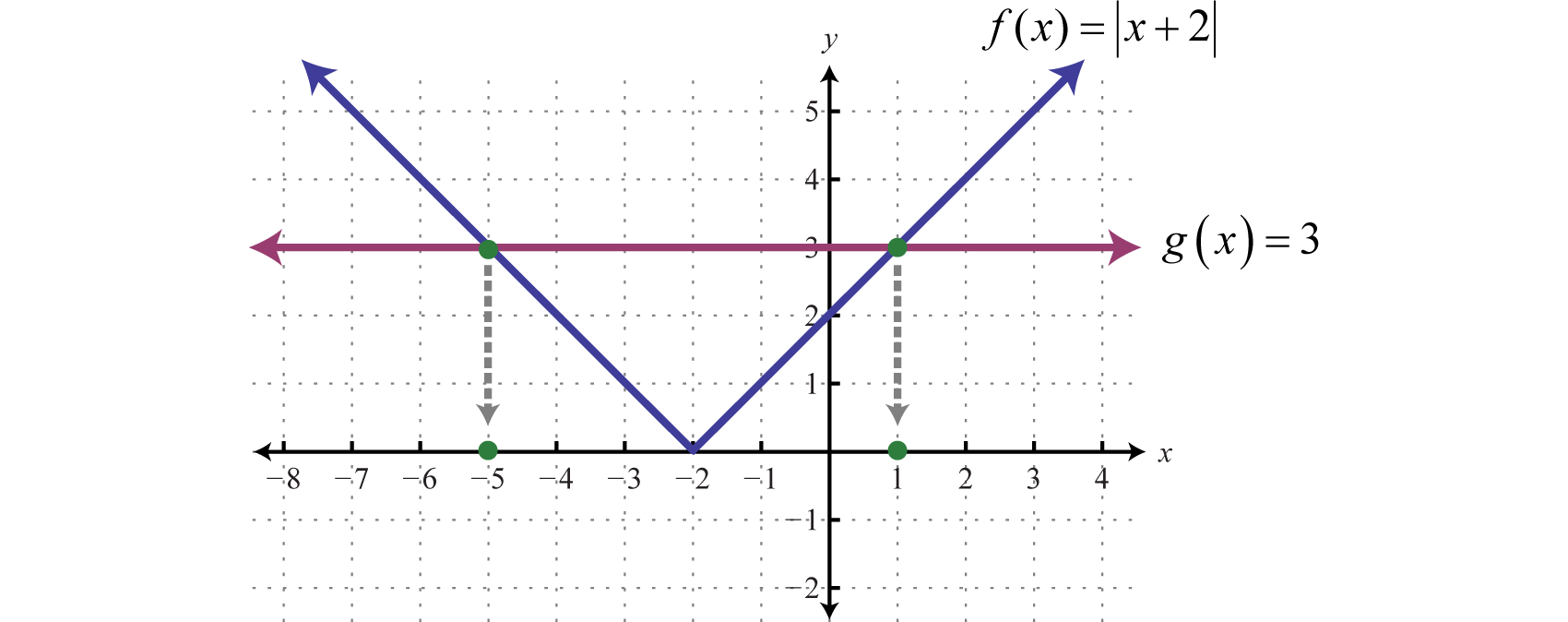
From the graph we can see that both functions coincide where x = −5 and x = 1. The solutions correspond to the points of intersection.
Example 2
Solve:
Solution:
Here the argument of the absolute value is and can be equal to −4 or 4.
Check to see if these solutions satisfy the original equation.
Check |
Check |
|---|---|
Answer: The solutions are and
To apply the theorem, the absolute value must be isolated. The general steps for solving absolute value equations are outlined in the following example.
Example 3
Solve:
Solution:
Step 1: Isolate the absolute value to obtain the form
Step 2: Set the argument of the absolute value equal to ±p. Here the argument is and
Step 3: Solve each of the resulting linear equations.
Step 4: Verify the solutions in the original equation.
Check |
Check |
|---|---|
Answer: The solutions are −1 and
Not all absolute value equations will have two solutions.
Example 4
Solve:
Solution:
Begin by isolating the absolute value.
Only zero has the absolute value of zero, In other words, has one solution, namely Therefore, set the argument equal to zero and then solve for x.
Geometrically, one solution corresponds to one point of intersection.
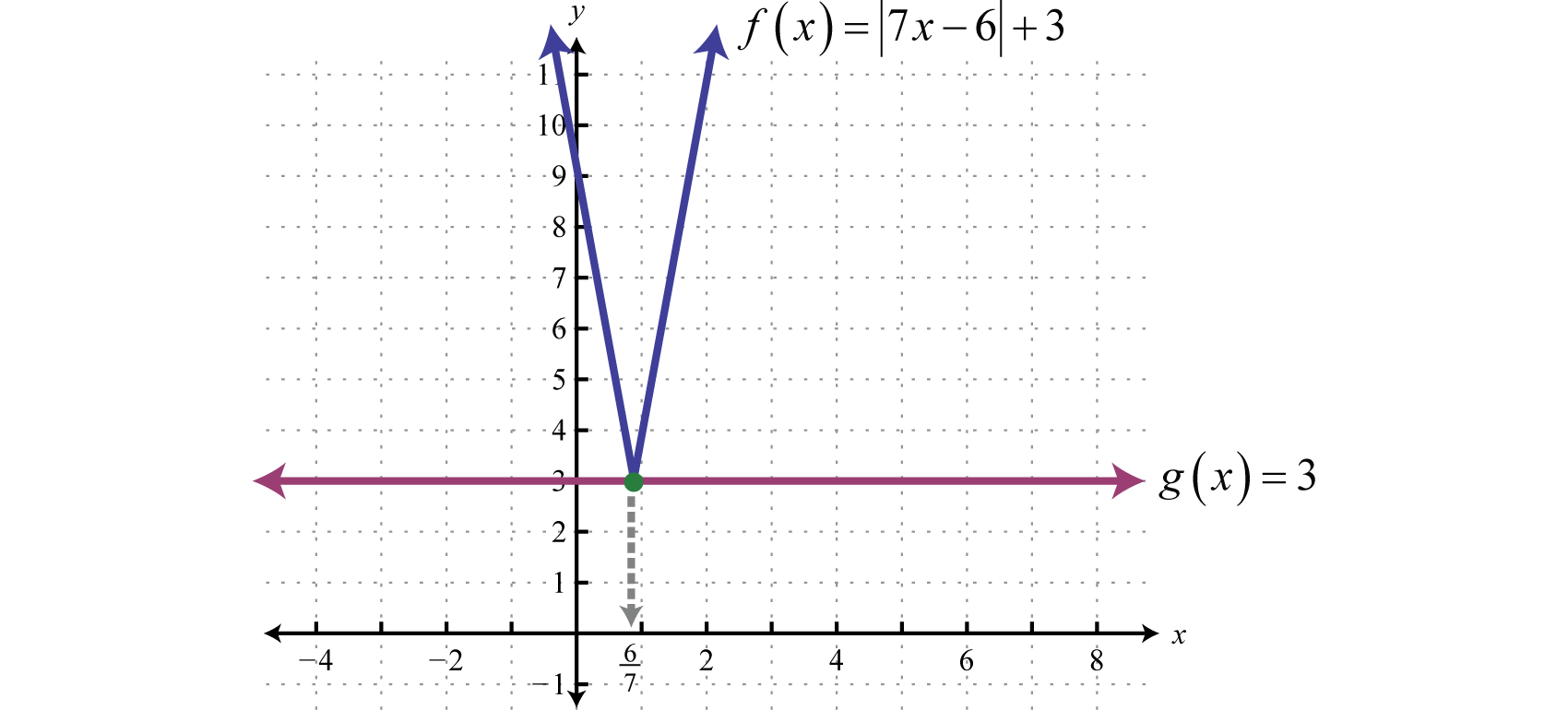
Answer: The solution is
Example 5
Solve:
Solution:
Begin by isolating the absolute value.
In this case, we can see that the isolated absolute value is equal to a negative number. Recall that the absolute value will always be positive. Therefore, we conclude that there is no solution. Geometrically, there is no point of intersection.
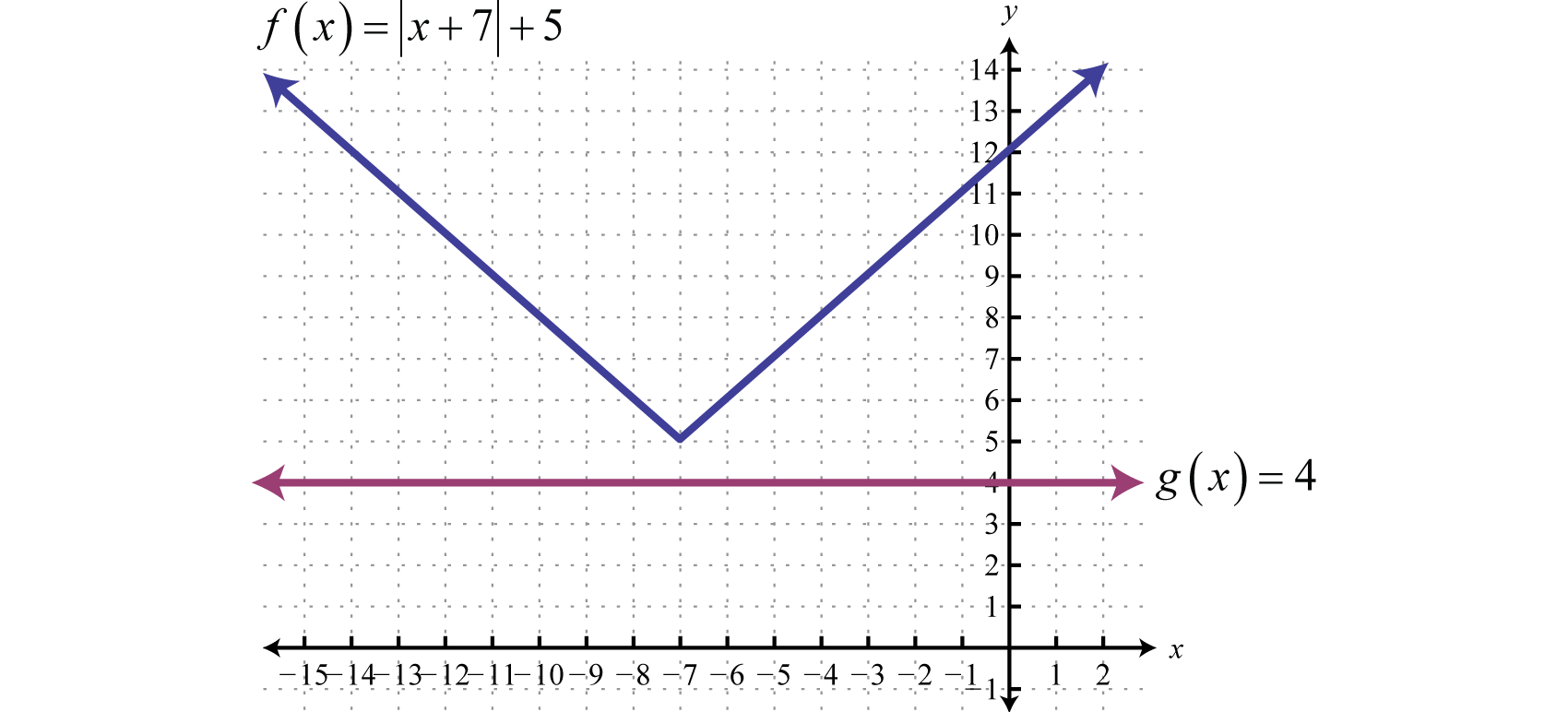
Answer: There is no solution, Ø.
If given an equation with two absolute values of the form , then b must be the same as a or opposite. For example, if a = 5, then b = ±5 and we have:
In general, given algebraic expressions X and Y:
In other words, if two absolute value expressions are equal, then the arguments can be the same or opposite.
Example 6
Solve:
Solution:
Set equal to and then solve each linear equation.
To check, we substitute these values into the original equation.
Check |
Check |
|---|---|
As an exercise, use a graphing utility to graph both and on the same set of axes. Verify that the graphs intersect where x is equal to 1 and 3.
Answer: The solutions are 1 and 3.
Absolute Value Inequalities
We begin by examining the solutions to the following inequality:
The absolute value of a number represents the distance from the origin. Therefore, this equation describes all numbers whose distance from zero is less than or equal to 3. We can graph this solution set by shading all such numbers.

Certainly we can see that there are infinitely many solutions to bounded by −3 and 3. Express this solution set using set notation or interval notation as follows:
In this text, we will choose to express solutions in interval notation. In general, given any algebraic expression X and any positive number p:
This theorem holds true for strict inequalities as well. In other words, we can convert any absolute value inequality involving “less than” into a compound inequality which can be solved as usual.
Example 7
Solve and graph the solution set:
Solution:
Bound the argument by −3 and 3 and solve.
Here we use open dots to indicate strict inequalities on the graph as follows.

Answer: Using interval notation,
The solution to can be interpreted graphically if we let and and then determine where by graphing both f and g on the same set of axes.
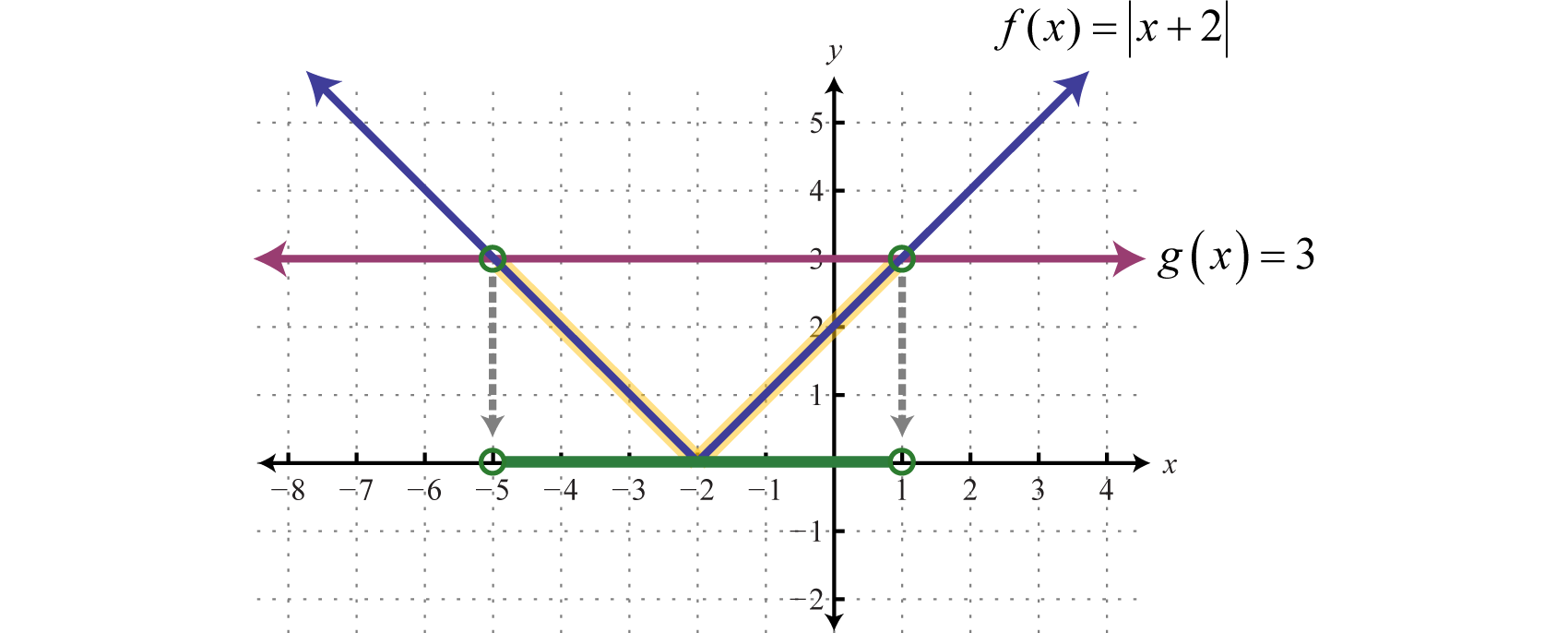
The solution consists of all x-values where the graph of is below the graph of In this case, we can see that where the x-values are between −5 and 1. To apply the theorem, we must first isolate the absolute value.
Example 8
Solve:
Solution:
Begin by isolating the absolute value.
Next, apply the theorem and rewrite the absolute value inequality as a compound inequality.
Solve.
Shade the solutions on a number line and present the answer in interval notation. Here we use closed dots to indicate inclusive inequalities on the graph as follows:

Answer: Using interval notation,
Next, we examine the solutions to an inequality that involves “greater than,” as in the following example:
This inequality describes all numbers whose distance from the origin is greater than or equal to 3. On a graph, we can shade all such numbers.
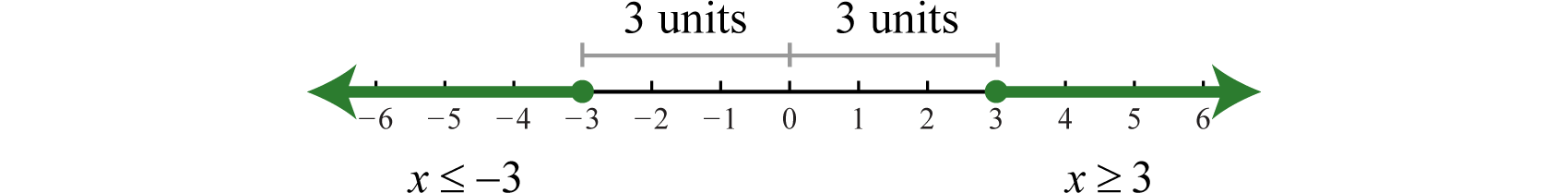
There are infinitely many solutions that can be expressed using set notation and interval notation as follows:
In general, given any algebraic expression X and any positive number p:
The theorem holds true for strict inequalities as well. In other words, we can convert any absolute value inequality involving “greater than” into a compound inequality that describes two intervals.
Example 9
Solve and graph the solution set:
Solve
The argument must be less than −3 or greater than 3.
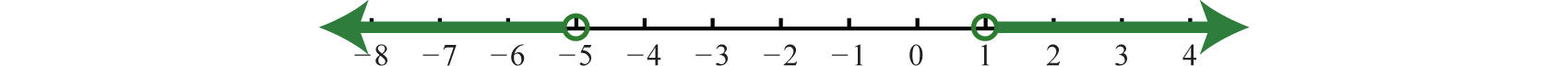
Answer: Using interval notation,
The solution to can be interpreted graphically if we let and and then determine where by graphing both f and g on the same set of axes.
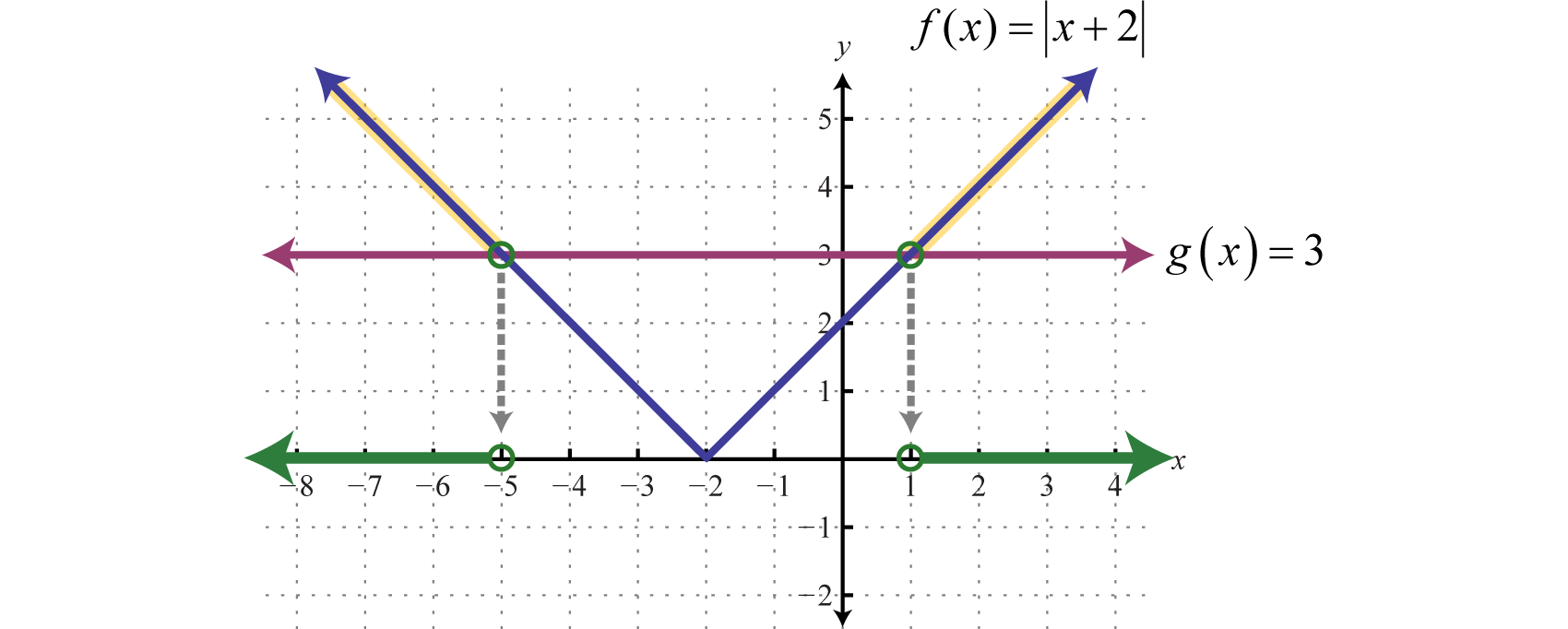
The solution consists of all x-values where the graph of is above the graph of In this case, we can see that where the x-values are less than −5 or are greater than 1. To apply the theorem we must first isolate the absolute value.
Example 10
Solve:
Solution:
Begin by isolating the absolute value.
Next, apply the theorem and rewrite the absolute value inequality as a compound inequality.
Solve.
Shade the solutions on a number line and present the answer using interval notation.

Answer: Using interval notation,
Up to this point, the solution sets of linear absolute value inequalities have consisted of a single bounded interval or two unbounded intervals. This is not always the case.
Example 11
Solve and graph:
Solution:
Begin by isolating the absolute value.
Notice that we have an absolute value greater than a negative number. For any real number x the absolute value of the argument will always be positive. Hence, any real number will solve this inequality.

Geometrically, we can see that is always greater than
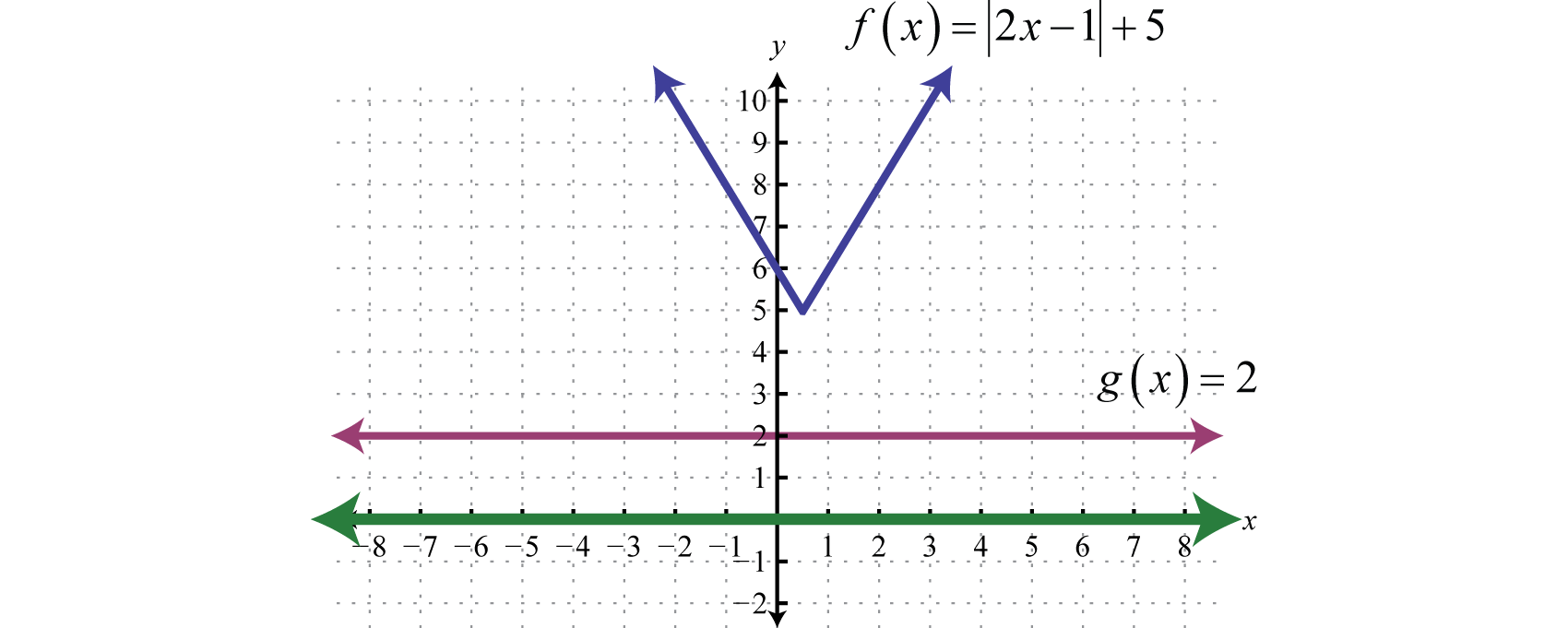
Answer: All real numbers,
Example 12
Solve and graph:
Solution:
Begin by isolating the absolute value.
In this case, we can see that the isolated absolute value is to be less than or equal to a negative number. Again, the absolute value will always be positive; hence, we can conclude that there is no solution.
Geometrically, we can see that is never less than
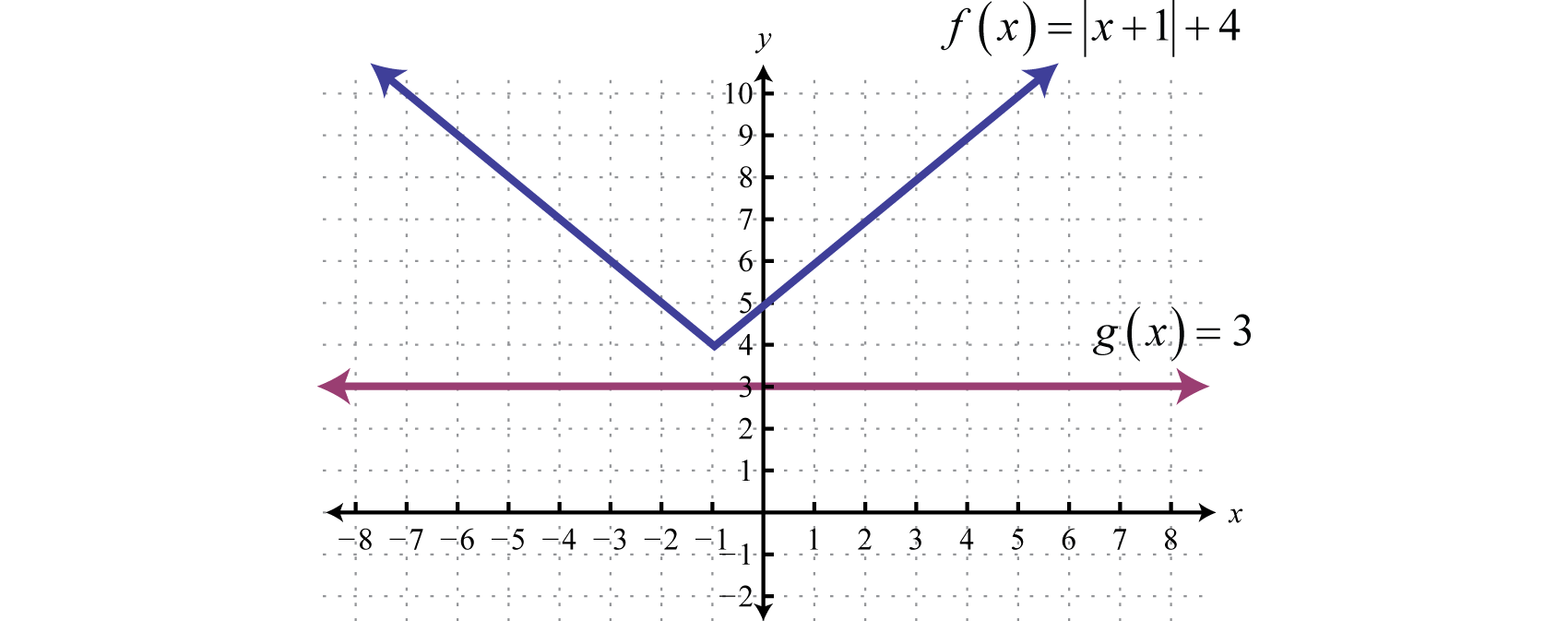
Answer: Ø
In summary, there are three cases for absolute value equations and inequalities. The relations =, and determine which theorem to apply.
Case 1: An absolute value equation:
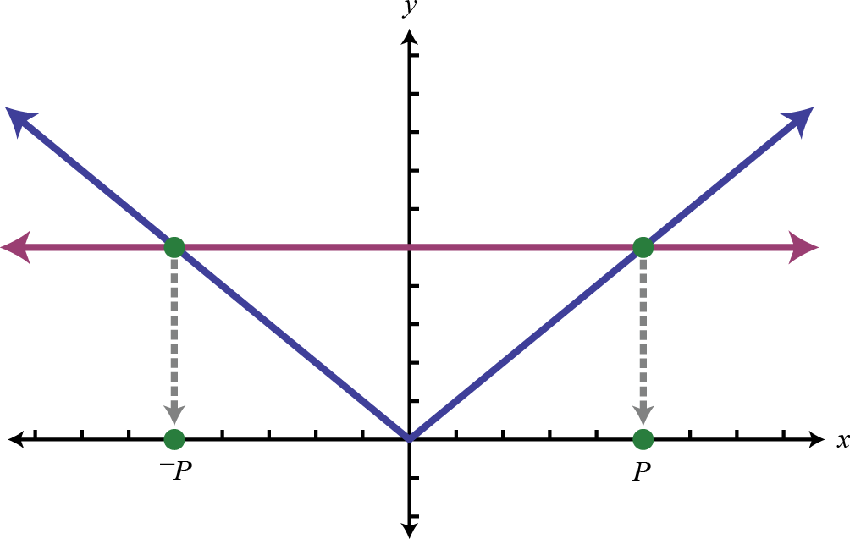
|
Case 2: An absolute value inequality involving “less than.”
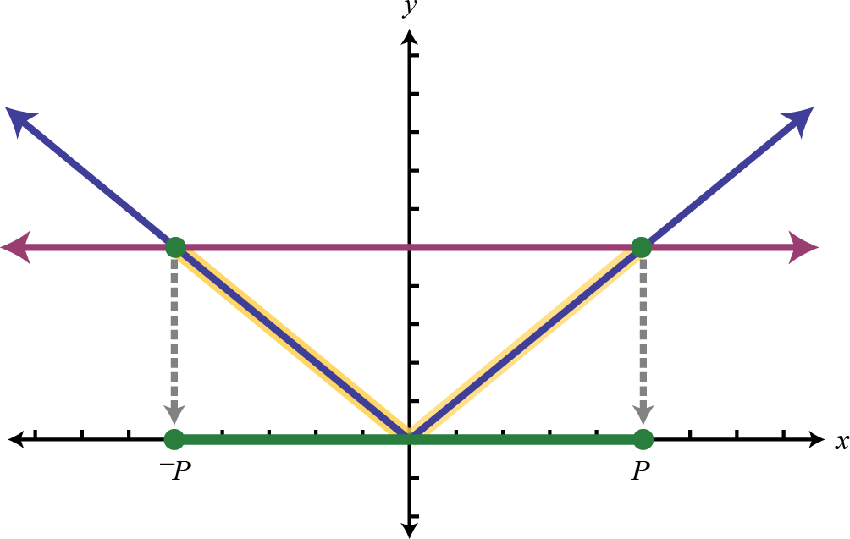
|
Case 3: An absolute value inequality involving “greater than.”
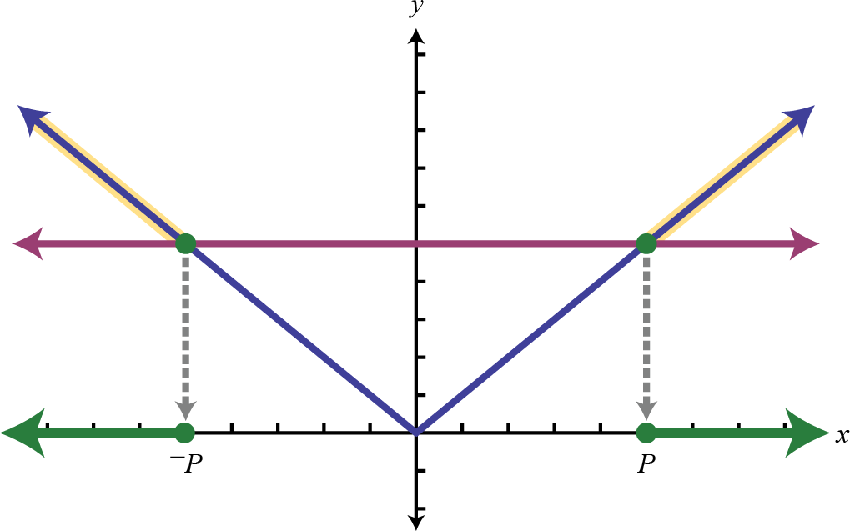
|
Key Takeaways
- To solve an absolute value equation, such as , replace it with the two equations and and then solve each as usual. Absolute value equations can have up to two solutions.
- To solve an absolute value inequality involving “less than,” such as , replace it with the compound inequality and then solve as usual.
- To solve an absolute value inequality involving “greater than,” such as , replace it with the compound inequality and then solve as usual.
- Remember to isolate the absolute value before applying these theorems.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solve for x:
-
Solve for x:
Part A: Absolute Value Equations Solve.
Assume all variables in the denominator are nonzero.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solve for x where :
-
Solve for x where :
-
-
-
-
Part B: Absolute Value Inequalities
Solve and graph the solution set. In addition, give the solution set in interval notation.
Solve and graph the solution set.
Assume all variables in the denominator are nonzero.
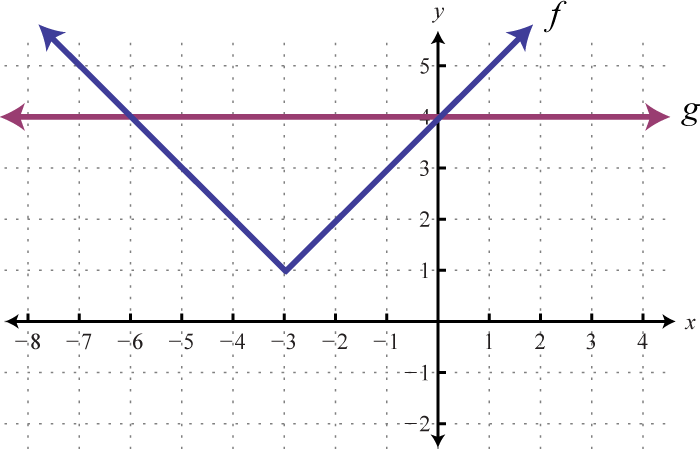
Given the graph of and , determine the x-values where:
-
Make three note cards, one for each of the three cases described in this section. On one side write the theorem, and on the other write a complete solution to a representative example. Share your strategy for identifying and solving absolute value equations and inequalities on the discussion board.
-
Make your own examples of absolute value equations and inequalities that have no solution, at least one for each case described in this section. Illustrate your examples with a graph.
Part C: Discussion Board
Answers
-
−9, 9
-
-
4, 10
-
-
−12
-
-
Ø
-
-
−6, 7
-
-
−1,
-
-
1,
-
-
−26, 10
-
-
0, 6
-
-
0,
-
-
-
-
1, 15
-
-
Ø
-
-
−3, 1
-
-
4, 6
-
-
Ø
-
-
−2.2, 7.8
-
-
-
-
1, 5
-
-
-
-
, 5
-
-
, 1
-
-
−4, 0.75
-
-
0, 4
-
-
-
-
;

-
-
;
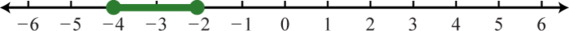
-
-
Ø;
-
-
;

-
-
;

-
-
;

-
-
;
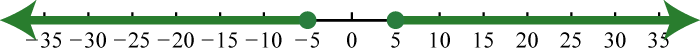
-
-
;
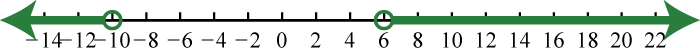
-
-
;

-
-
;
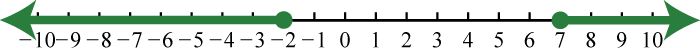
-
-
;
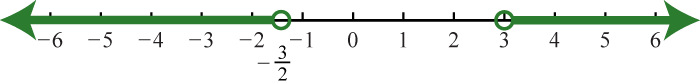
-
-
;
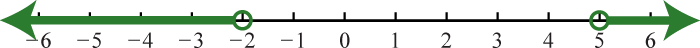
-
-
;
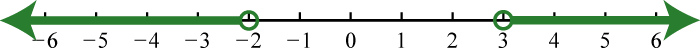
-
-
;

-
-
;

-
-
;
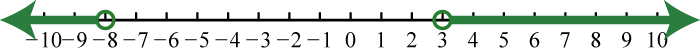
-
-
;
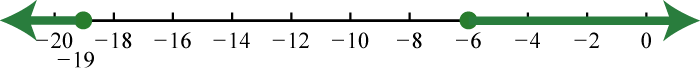
-
-
;

-
-
;

-
-
;
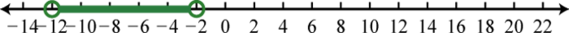
-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
;

-
-
-
-
- −6, 0;
- ;
-
-
- Ø;
- ;
- Ø
-
-
Answer may vary
-